近況報告
5月以来更新が滞っており,大変遺憾です(?)。本業のお仕事が少し多忙になってきたことと,7月あたりから諸事情につきスウェーデン語を学び始めたため(主にDuolingoにて),車輪形倒立振子の開発やLTspiceの勉強への興味関心が一時的に置き去りになってしまいました。
そんな中でもESP32*1だけでなくRP2040も使えるようになると今後の幅が広がりそうですので,図1のようにXIAOを衝動買いしたりと細々と活動しています。少しずつですが電気電子・制御工学の世界にも復帰したいと思っています。年末までに車輪形倒立振子を立てるという目標はまだ放棄しないでおこう…!

*1:これも表面を撫でただけの使い方しか知りませんが…。
Pythonによる車輪形倒立振子の線形化と最適レギュレータ
はじめに
P計画
Pythonの数式処理ライブラリSymPyには力学系を取り扱うためのsympy.physics.mechanicsというモジュールがあります(以降,“SymPy Mechanics”とも呼びます)。本ブログでは前回,このSymPy Mechanicsの仕組みを活用して車輪形倒立振子の運動方程式を導出しました。
前回の最後に「次回はシミュレーションとアニメーションを扱う」と宣言していましたが,やはり,(i) 線形制御理論を活用した制御設計のためには線形化による状態空間モデルが必須であるとの思いから,また,(ii) SymPy Mechanicsには運動方程式を線形化する仕組みも備わっていることから,今回はまず線形化について記述することにします。その後,SymPyの結果をLambdifyなどによって数値化(具体的なパラメータ例を代入して,NumPyから活用できるようにすること)し,SciPyからこれを活用することによるシミュレーションとアニメーションについて述べていきます。
ここまで来れば,実機の設計・製作の前に解決しておくべき課題は,加速度・ジャイロセンサの出力信号を用いた状態の推定と,DCモータのモデル化・制御になりますでしょうか。
完成イメージ
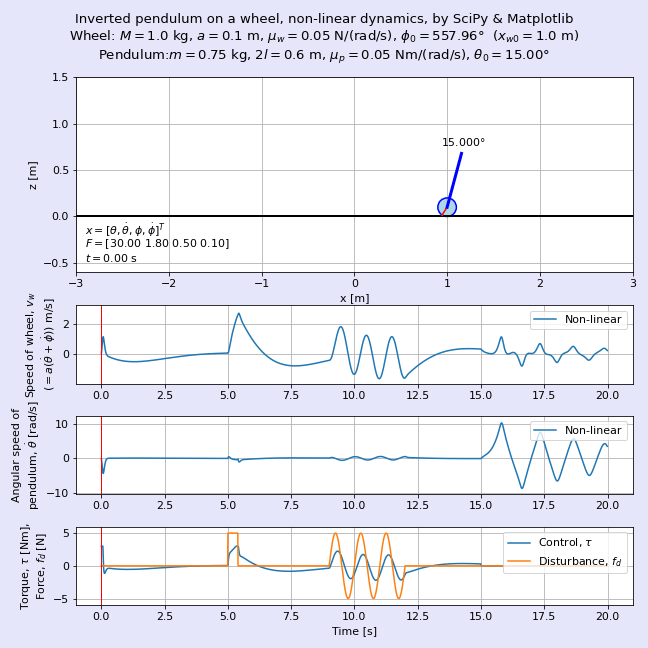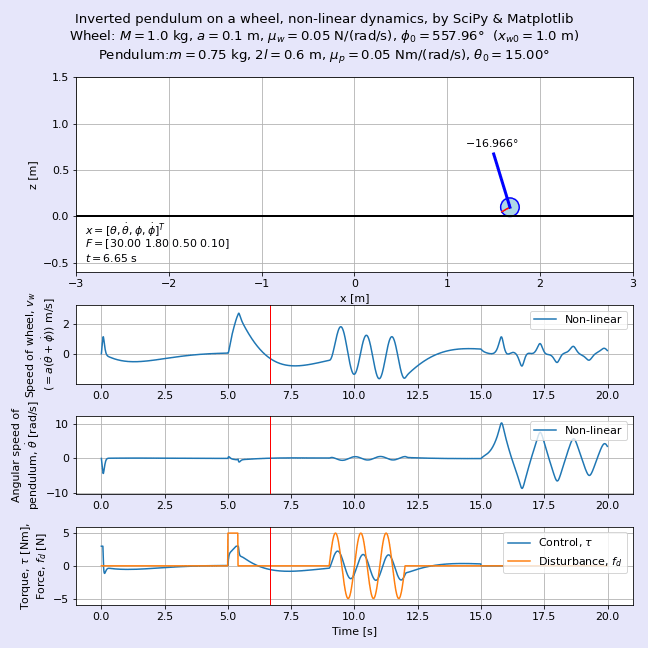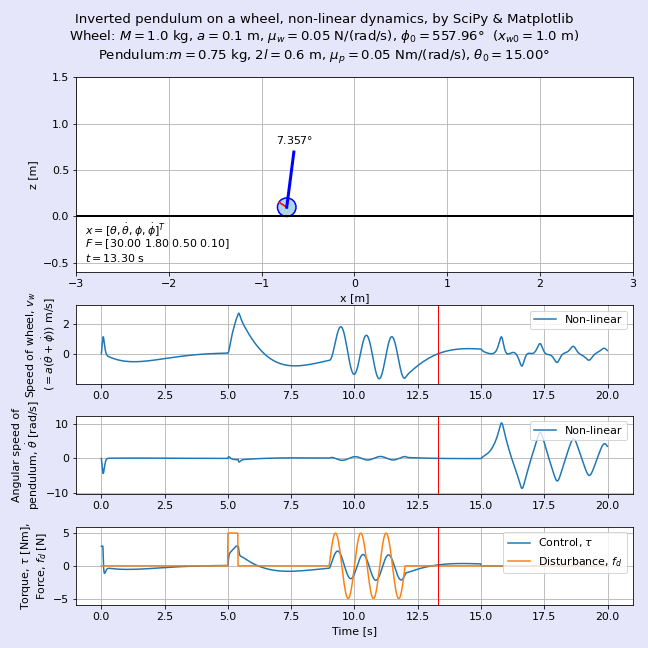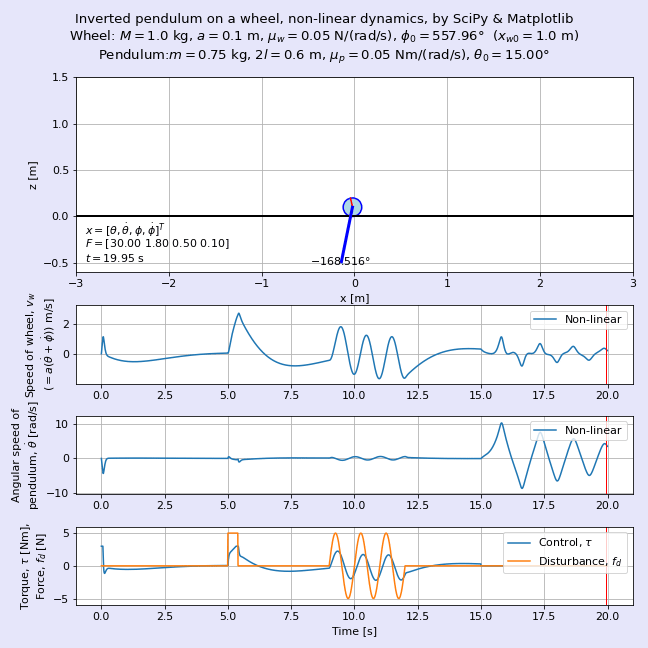
図1に完成したアニメーションを示します。図2に非線形な系である車輪形倒立振子の非線形な元のモデルとそれを線形化した状態空間モデル(「線形化モデル」とも呼ぶことにします)の挙動を重ねて表示したアニメーションを示します。車輪の質量M = 0.75 kg,車輪の半径a = 0.1 m,振り子の質量m = 1.5 kg,振り子の長さ2l = 0.6 mであり,車輪の初期位置xw0 = 1 m,振り子の初期角度θ0 = 15°の動きを可視化しています。よく見るとゴーストのように薄い色の車輪と振り子がほぼ重なって動いていますが,この色が薄い方が線形化モデルです。

ここでは線形化モデルに基づいて最適レギュレータ(LQR, linear quadratic regulator)の設計方法によって求めた状態フィードバックゲインを用いて倒立させており,時刻t = 5 sから0.5秒間のステップ状の外乱,時刻t = 8 sからの正弦波状の外乱にも負けずに倒立を維持している様子が見えますね。
時刻t = 15 s以降は制御を止めます。当たり前ですが振り子の倒立が維持できなくなり,非線形な元のモデルでは逆さまになってぶらぶらと振動します。一方の線形モデルでは高速回転しながらはるか彼方へふっ飛んでいきます。吉田勝俊先生の「短期集中:振動論と制御理論」(日本評論社,2003年)のp. 71の脚注にある通り,「線形化してしまったので,回転しないで発散する」を体現していますね。
いずれにしても本記事は筆者個人としての現代制御理論の初歩の学び直しのための備忘録のようなものであり,学術的に何ら新規性のある記述はしていませんのでご了承下さい。本記事独自の特長があるとすれば,SymPy Mechanicsの仕組みを活用した運動方程式の線形化の例題の1つとして,和文での記事である点,と言えるでしょうか。
続きを読むPythonによる車輪形倒立振子の運動方程式の導出
はじめに
P計画
前々回,前回にて台車形倒立振子の運動方程式を導出し,シミュレーション,アニメーション,線形化,最適レギュレータの作り方について書き散らして参りました。本記事以後,いよいよ台車形から車輪形の倒立振子に歩みを進め,運動方程式の導出,シミュレーション,アニメーションについて書いていきます。ただし本記事では紙面(?)の都合上,SymPyにおいて力学系をシステマティックに取り扱うsympy.physics.mechanicsというモジュールを用いた運動方程式の導出に焦点を当て,シミュレーションとアニメーションは次回に譲りたいと思います。
まだまだシミュレーションでしかありませんが,ここで制御設計についての理解を深めてから実機の設計・製作,ソフトウェア実装を進め,願わくば年末頃には実際の車輪形倒立振子を立てることができればと夢想しております。
完成したアニメーション
運動方程式を導出したらそれをSciPyで解き,Matplotlibにてアニメーションにします。図1に完成した車輪形倒立振子のアニメーションを示します。車輪の質量M = 0.2 kg,車輪の半径a = 0.1 m,振り子の質量m = 1.5 kg,振り子の長さ2l = 0.6 mであり,車輪の初期位置xw0 = 1 m,振り子の初期角度θ0 = 15°の動きを可視化しています。ここではトライ・アンド・エラーで求めた状態フィードバックゲインを用いて倒立させており,時刻t = 5 sから0.5秒間のステップ状の外乱,時刻t = 8 sからの正弦波状の外乱にも負けずに倒立を維持している様子が見えますね。時刻t = 15 s以降は制御を止めます。当たり前ですが振り子の倒立が維持できなくなり,逆さまになってぶらぶらと振動します。
力学的な観点からみると,車輪も振り子も剛体なので,一見して運動方程式は台車形*1より複雑になりそうです。本記事では数式処理ライブラリSymPyのsympy.physics.mechanicsモジュールを用いてシステマティックに運動方程式を導出することを試みます。
*1:台車を質点として取り扱っていました。
Pythonによる台車形倒立振子の線形化と最適レギュレータ
はじめに
P計画: 倒立振子の思ひ出
筆者のメインPCは11年物のSandy Bridge (Intel Core i7-2600K)を使用した骨董品です。そのHDDの奥底から,はるか昔の実験レポートが出土しました*1。今でも図1のようにMicrosoft Wordで開くことができます。
そう,筆者は過去に台車形倒立振子を触ったことがあったのでした。読み返してみると,非線形な運動方程式としてのシミュレーションはしておらず,ほぼいきなり線形化したモデルから始まっていました。ベルト駆動の台車をガタガタさせながら,鉄の棒を倒立させていたことを懐かしく思い出します。
完成イメージ
さて,前回を簡単に振り返りますと,車輪形倒立振子を設計・製作する前段階として,Pythonによる台車形倒立振子のシミュレーションを試みたのでした。具体的には台車形倒立振子の運動方程式(を基にした非線形状態方程式)を導出し,SciPyのsolve_ivp関数にて初期値問題を解き,Matplotlibにてアニメーションとして可視化しています。
本記事では,前回導出した非線形状態方程式を線形化して状態空間モデルを立て,アニメーションを作成します。
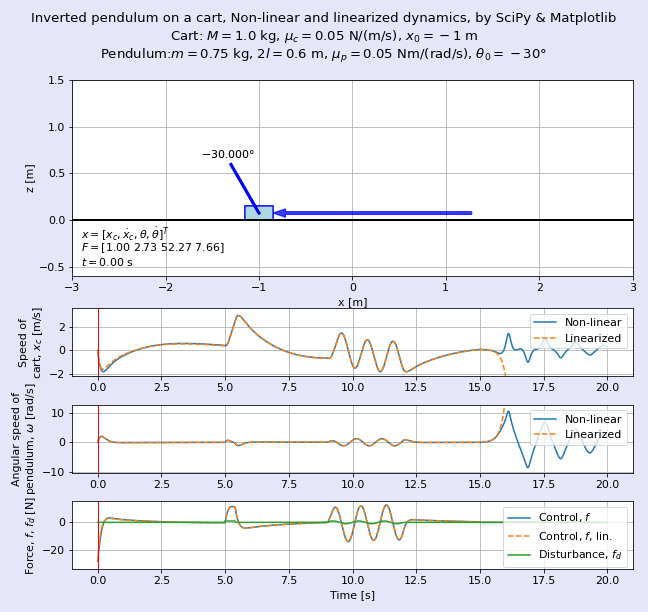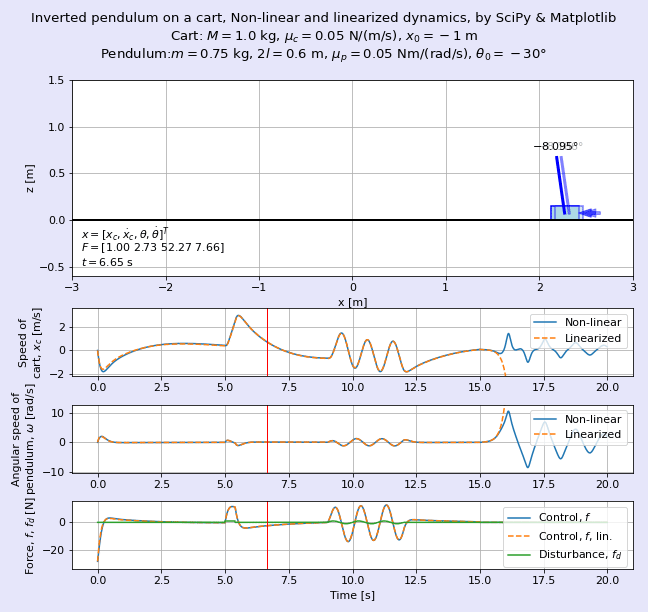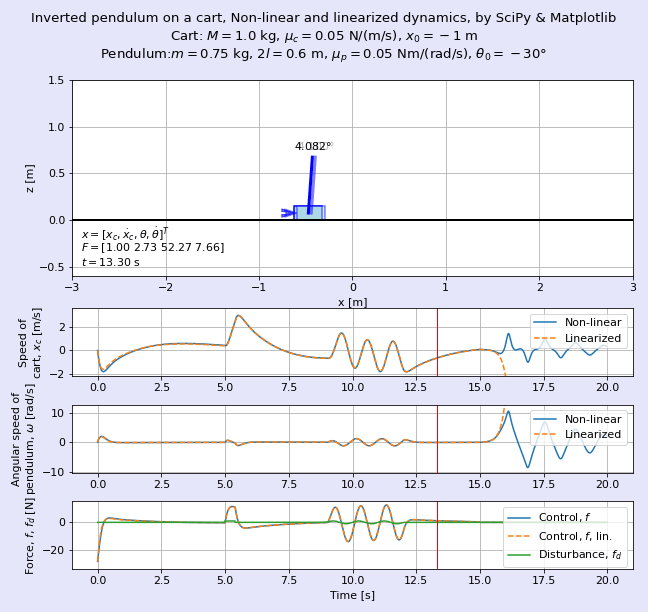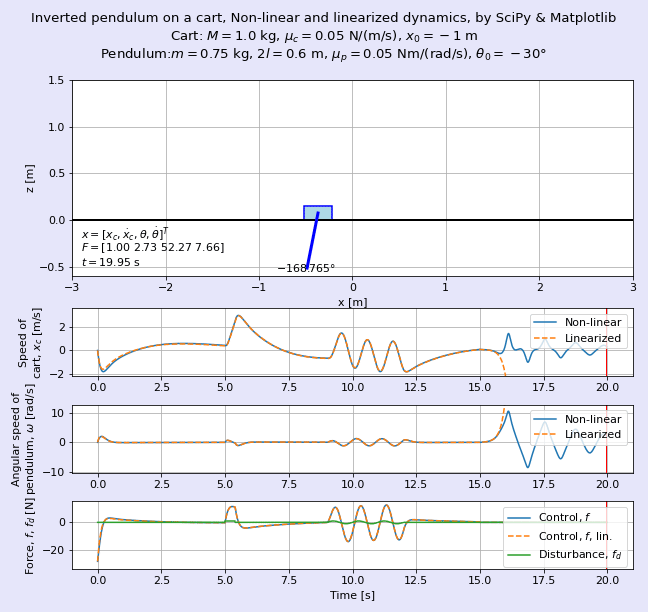
完成イメージとして,図2に非線形な系である台車形倒立振子とその線形化モデルの挙動を重ねて表示したアニメーションを示します。よく見るとゴーストのように薄い色の台車と振り子がほぼ重なって動いていますが,この色が薄い方が線形化モデルです。
筆者として長らく疑問であった点であり,また,制御工学に関する種々の教科書でもあまり言及されていない*2話題として,「線形化したモデルは,元の非線形なシステムのふるまいをどれだけ近似していると言えるのか」という問いがありました。図2のアニメーションは,台車形倒立振子について元の非線形な状態方程式と,それを線形化した状態空間モデルのふるまいを重ねて表示し,筆者の感覚的な理解の促進を狙ったものです。
図2では時刻t = 15 s以降で制御を止めているため,非線形な元の倒立振子は下向きに倒れてブラブラと揺れますが,線形化した倒立振子は高速回転しながらはるか彼方へふっ飛んでいきます。吉田勝俊先生の「短期集中:振動論と制御理論」(日本評論社,2003年)のp. 71の脚注にある通り,「線形化してしまったので,回転しないで発散する」を体現していますね。
本記事ではまた,SciPyのlinalg.solve_continuous_are関数を使って線形化した状態空間モデルに関するRiccati方程式を解き,最適レギュレータ(LQR, linear quadratic regulator)の設計を試みます。
いずれにしても本記事は筆者個人としての現代制御理論の初歩の学び直しのための備忘録のようなものであり,学術的に何ら新規性のある記述はしていませんのでご了承下さい。
図2を生成するJupyter NotebookをGitHubに起きましたので,適宜ご参照下さい。
続きを読むPythonによる台車形倒立振子のシミュレーション
はじめに
P計画
車輪形倒立振子を作る──この目標に対して問題を分解しながらアタックするため,前回にて床を転がる車輪のシミュレーションとアニメーションをPython (+ NumPy, SciPy, Matplotlib)で実現した経緯をまとめました。次は振り子をシミュレーションしようと思っていましたが,勢い余って(?)振り子だけでなく台車も含めた台車形倒立振子まで進むことができたので,今回はその様子について記述していきます*1。
床を転がる車輪とは異なり,台車形倒立振子では運動方程式がもろに非線形になります。本記事では非線形のままの運動方程式を表現するPythonの関数を定義し,SciPyのsolve_ivp関数にて初期値問題を解きます。また,これも前回同様にMatplotlibにて見て楽しい(!)アニメーションを生成します。運動方程式を整理する際にSymPyも用いています*2。
完成イメージ
図1に完成したアニメーションを示します。20秒間の現象をシミュレーションしております。振り子が180°,つまり真下を向いた状態から(テキトーな力を台車に加えた)振り上げ制御にて振り子を上向きに立てた後に,時刻t = 2 sにて状態フィードバック制御に入ります。

その後,時刻t = 7.5 sから0.5秒間,振り子の先端に外乱を加えていますが,状態フィードバックのおかげで転倒することなく倒立し続けていることが分かります。最後に時刻t = 12.5 s以降で制御を止めて無制御状態に移行すると,振り子は倒立できなくなって下向きにブラブラと減衰振動している様子が見て取れます。このアニメーションを生成するJupyter NotebookをGitHubに置きましたので適宜ご参照下さい。
アニメーションの作り方については前回とほぼ同様で,舞台を作ってから台車,振り子,力を表す矢印,時刻などの文字列のアーティストの属性(プロパティ)を書き換えながらフレームを生成し,HTML5のmp4動画やGIFアニメーションを生成しています。
*1:車輪と振り子の間でトルクが分配されることから,台車形倒立振子よりも車輪形倒立振子の方が複雑で難易度が高いのではないかと筆者は思っています。
*2:SymPyにはラグランジュ方程式を取り扱う機能もあるようで,SymPyのみで運動方程式を導くこともできるようです。いずれかの時点で挑戦してみます。
Pythonによる車輪のシミュレーションとアニメーション
はじめに
P計画
2023年を迎えて2月に入り,その2月も終盤に差し掛かろうとしています。三寒四温──もう春が近いですね…🌸 筆者が年初に思い描いた目標の1つに「車輪形倒立振子を作る」があります。ESP32等のマイコンモジュールとMPU6050等のジャイロセンサ,モータドライバIC,DCモータと車輪を組み合わせれば,ハードウェアとしては(拙いながらも)作ることだけはできそうです。実際,昨年に荒い試作をしてみましたが,残念ながら倒立する気配はありませんでした。
やはり,まずは数理モデルを構築し,現代制御理論に立脚した制御設計を経てこそ,倒立振子の真の醍醐味を得られるのではないか──?
このような訳で,いきなり実機を作ることはやめ,まずはシミュレータを作ろうと思い立ちました。と言っても,いきなり車輪形倒立振子全体のシミュレータを作るのはハードルが高い,また,車輪形倒立振子の出来上がった運動方程式を他所からコピー & ペーストしてきても勉強にならないので,数学弱者たる筆者が理解できる範囲を少しずつ広げるため,段階を追うことにしました。

まず今回は,トルクを与えられて床面を転がる車輪をモデル化し,シミュレーション,そして可視化のためにアニメーションを作ることにします。上の図1が完成したアニメーションになります。次回以降,振り子やDCモータなどにモデル化の範囲を広げていき(途中で台車形倒立振子のシミュレータも作ります),最終的には車輪形倒立振子のシミュレーション,アニメーションを作り,実機の設計に繋げていきます。
科学計算ツール
「トランジスタ技術」2020年7月号の記事(参考文献1)にて早川槙一さんがLTspiceを使った車輪形倒立振子のシミュレータを構築し,かつ,OPアンプによるアナログ制御を実現するという刺激的な挑戦をされていました。これを拝読したときから,筆者の中で倒立振子を作ろうという機運が高まってきたと言えます。技術者のはしくれとして,倒立振子ぐらい立たせたいではないか!
筆者もLTspiceの取り扱いにはある程度慣れているつもりですが,LTspiceでは時間波形の表示しかできず,車輪なり倒立振子なりが動いている様子をアニメーションさせることはできません。やはり目で見て楽しい(!)シミュレータを目指したいので,微分方程式(運動方程式)の求解とアニメーションをPython*1で組んでみることにしました*2。
この分野には優れた先賢たちが幾多の書籍,論文,ウェブサイト,ブログ記事,動画などに記録を残しているため,本記事が何か新しいことを提供できているかは不明ですが,ひとまず続けていこうと思います。
Jupyter Notebook
本記事のために作成したJupyter NotebookをGitHubに置きました。適宜ご参照下さい。
*1:およびNumPy, SciPy, Matplotlib, JupyterLab
*2:もちろんMATLAB/SimulinkやScilabなど,他にも選択肢はあります。MATLAB Homeはとても心惹かれるものがありますね…。
2次遅れ系の時間応答と減衰係数ζについての素朴な疑問
はじめに
今回は古典制御理論の初歩的なある事柄に関して筆者が抱いていた素朴な(あるいは幼稚な)疑問に関する書き散らしとなっています。あらかじめご了承下さい。
さて,2次遅れ系
のインパルス応答やステップ応答は,減衰係数ζ (> 0)の値によって3つに場合分けされることが広く知られています。この3つは特性方程式((1)式の分母 = 0)の解p1, p2に対応しており,それぞれ
- ζ < 1(p1, p2が共役複素数解)の場合,振動しながら減衰・収束する(不足制動)
- ζ = 1(p1, p2が重解)の場合,1と3の臨界状態(臨界制動)
- ζ > 1(p1, p2が異なる2つの実数解)の場合,振動することなく減衰・収束する(過制動)
のようになります。

図1に例としてK = 1,ωn = 1に固定し,ζを0.1から2.0まで変化させた場合における2次遅れ系のインパルス応答,ステップ応答,およびボード線図を示します。
上記の3つの条件におけるインパルス応答やステップ応答を表す数式を一見すると,後述のようにかなり形が異なって見えます。しかし,ζが1を跨ぐ前後においても時間応答の変化は滑らかに見えます。これは一体どうしてでしょうか? こんな疑問がもやもやとしていました。
続きを読む