LTspiceによる三相PWM整流器の上位制御とノーズカーブ

はじめに

サイリスタの転流を交流側の電圧に依存している他励インバータでは，電力系統（以下，単に「系統」とも呼びます）の短絡容量が小さくなると（＝系統が弱いと）安定運転が難しくなると言われています。これに対して，IGBT (insulated-gate bipolar transistor)などのオンオフ制御バルブデバイス（自己消弧素子）を用いる自励インバータでは，系統の短絡容量が小さくても運転できるとされています。とは言うものの，系統の短絡容量と自励インバータの定格電力*1の比であるSCR (short-circuit ratio)が1.5 ~ 2を下回ると，やはり安定性に問題が生じる恐れがあることが指摘されています。

本記事では，本ブログでこれまで取り扱ってきたLTspiceによる三相PWM整流器に，有効電力制御，無効電力制御，交流電圧制御の制御ブロックを追加します。これら3つの制御と直流電圧制御とを合わせて，上位制御系と呼ぶことにします。

また，有効・無効電力制御とSCRの関係について，ノーズカーブの観点から若干の考察を加えます。ノーズカーブとは，系統の電圧安定性を検討する際に描かれる図です（P-V曲線，P-Vカーブとも呼ばれます）。SCRが小さい（＝系統が弱い）場合，三相PWM整流器（自励インバータ）の制御がいかに理想的であったとしても，ある有効電力を超えて受電することはできません。大きな有効電力を得ようと電流を増加させていくと，ある点で連系点の電圧が急激に低下してしまいます。これを電圧崩壊(voltage collapse)と呼びます。これは私の単なる憶測に過ぎませんが，上位制御系の不安定と，単なる電圧崩壊が，これまであまり区別されてこなかったのではないかという思いがあります*2。

本記事はそこで終わりですが，今後，上位制御を含めた三相PWM整流器の小信号モデルを立て，安定性の近似理論解析とLTspiceでの挙動の比較考察に移っていきたいと考えています。

シミュレーション例

文字ばかりの議論でなんのこっちゃいという感想が湧いてくる頃だと推察します。そこでまずはシミュレーション例を示します。まず，本ブログで従来取り扱ってきた三相PWM整流器のスキマティック（モデル）において，d-q座標系での電流制御を階層ブロック化し，さらに上位制御を追加します。次に，ノーズカーブを描いて，電圧崩壊する場合としない場合のシミュレーション結果との対応について述べます。

電流制御の階層ブロック化と上位制御の追加

図1に，上位制御を追加した三相PWM整流器のLTspiceスキマティックの全体を示します。また，図2，3に電流制御と上位制御の階層ブロックを示します。本ブログではこれまで，直流電圧制御を除いて，d-q座標系での電流制御の上位に制御系を設けていませんでした。しかし，実際には有効電力や無効電力を（連系点の電圧が変化しても）所望の値に保つためにフィードバック制御が存在します。これまでのモデルが煩雑に（画面上で広く複雑に）なって参りましたので，電流制御を階層ブロック化し，空いたスペースに上位制御を作ることにしましたが，見通しをよくするために上位制御も階層ブロックとすることにしました。

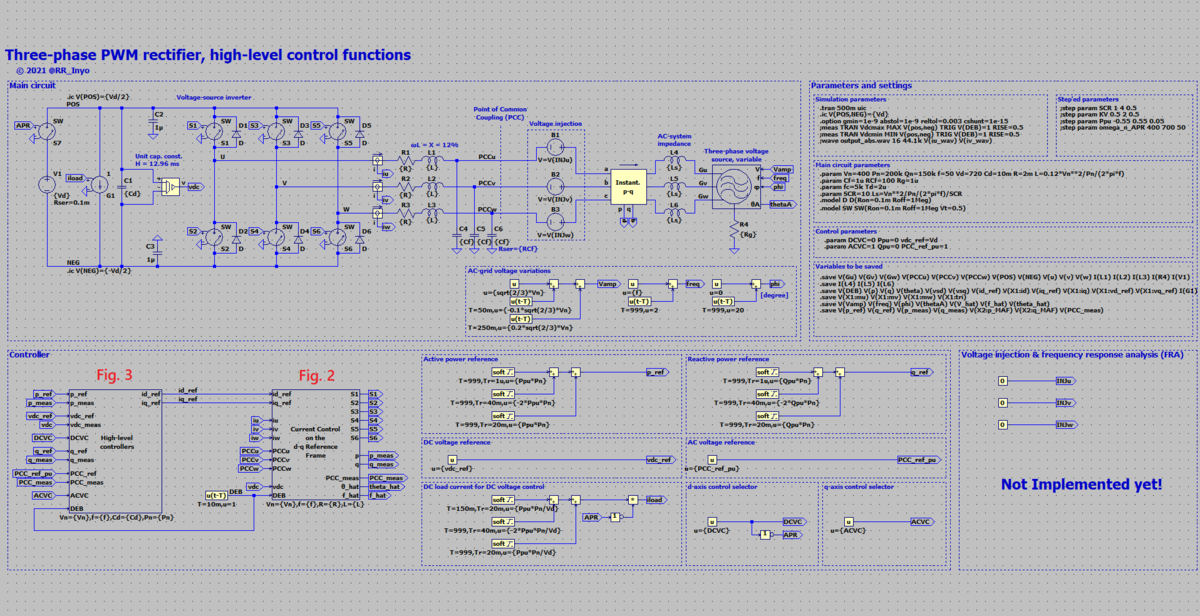
f:id:s-inoue2010:20210726190439p:plain — 図1: 上位制御を追加した三相PWM整流器のLTspiceスキマティック

f:id:s-inoue2010:20210726185346p:plain — 図2: 電流制御の階層ブロック

f:id:s-inoue2010:20210726185632p:plain — 図3: 上位制御の階層ブロック

どことなく本格化してきたように見えますゾ…？

電圧崩壊する場合としない場合

図4，5に2つのシミュレーション波形を示します。いずれもPWM整流器のゲートデブロック後，P = 0 kWから200 kWまで有効電力を立ち上げる（有効電力指令値を0 kWから200 kWにステップ変化させる）際の波形です。なお，Q = 0 kvar，つまり力率1運転です。また，PWM整流器と言いながら，直流側には720 Vの理想直流電圧源を接続しています。要するに，ただの系統連系自励インバータとして制御しています。

f:id:s-inoue2010:20210727022349p:plain — 図4: P = 200 kW，Q = 0 kvar，SCR = 3の場合のシミュレーション波形

f:id:s-inoue2010:20210727022439p:plain — 図5: P = 200 kW，Q = 0 kvar，SCR = 1.9の場合のシミュレーション波形

さて，図4は安定運転できているように見えますが，図5は何やら怪しい動きをしています。図5では電流（d軸電流）が増加し続けているにも関わらず，有効電力が200 kWにぎりぎりですが到達していません。さらに，連系点電圧の基本波実効値V(pcc_meas)（上から2段目，青色）が下がり続けています。すなわち，有効電力を0 kWから200 kWに立ち上げようとして電流を増加させると，連系点電圧が下がってしまい（電流増加のペースよりも電圧低下のペースが速い──とも表現できるとも思います），結果的に所望の有効電力が得られないまま電流増加，電圧低下が継続しています。このままシミュレーションを続ければ電圧崩壊に至ります（.tran解析を400 msで止めてしまいました）。

図4と図5の違いはSCRです。図4ではSCR = 3.0でしたが，図5ではSCR = 1.9としました。SCRを小さくしたことによって“制御が不安定になった”のでしょうか？

SCRとノーズカーブ

SCRとリアクタンスX

さて，改めて，SCRとは次式のように注目している機器・サブシステム（ここではもちろん三相PWM整流器（自励インバータ）です）の定格電力P_nomの系統の短絡容量S_scに対する比です。

$\mathrm{SCR} = \displaystyle \frac{S_{sc}}{P_{\mathrm{nom}}} \tag{1}$

SCRが大きいほど「強い系統である」，あるいは「理想電圧源に近い」ことを示す指標です。ここで，図6のような系統を考えます。無限大母線EからリアクタンスXを介して受電点に接続されている負荷が，ある有効電力P，無効電力Qを要求しています。その負荷の定格電力をP_nomとしましょう。また，この系統の定格（公称）電圧をV_nomとします*3。なお，系統インピーダンスは本来，実部も虚部も有する（さらに言えば三相不平衡や非線形性もある）ものですが，ここでは簡単のため，単純なリアクタンスXであると仮定します。また，受電点の電圧をVとし，Eを基準とした位相角をδとします。

f:id:s-inoue2010:20210727015949p:plain:w300 — 図6: 無限大母線とP-Q負荷

さて，SCRとXの関係は次式となります。

$X =\displaystyle \frac{Z_{\mathrm{base}}}{\mathrm{SCR}} = \frac{V_{\mathrm{nom}}^{2}}{P_{\mathrm{nom}} \cdot \mathrm{SCR}} \tag{2}$

Z_baseは基準インピーダンス(V_nom² / P_nom)です。SCRはp.u.表現でのインピーダンス（ここではリアクタンス）の逆数であるとも言えますね。

力率1運転の場合のノーズカーブ

図6の系統で，受電点の有効電力Pを大きくしていった場合，リアクタンスXでの電圧降下が生じるため，受電点電圧Vの実効値|V|は低下していきます。|V|が低下する中で一定のPを受電しようとすると，電流を増加せざるを得ません。するとXでの電圧降下がさらに大きくなります。場合によっては破綻する恐れがありそうです（後述のように電圧崩壊と呼ばれます）。Pと|V|（以降では誤解を招く恐れが無い場合は実効値|V|もVと表記します）の関係を表した図がノーズカーブ（P-V曲線，P-Vカーブとも呼ばれます）です。ノーズカーブの導出については付録にて簡単に触れます。

f:id:s-inoue2010:20210728015500p:plain — 図7: 力率1 (φ = 0°)の場合のノーズカーブ

図7に，力率1（力率角φ = 0°）である場合のノーズカーブを示します。SCRが0.5 ~ 5.0の場合について複数の曲線を描きました。横軸が有効電力P，縦軸が受電点の電圧Vです。系統（背後電源）の電圧は400 Vです。

P = 200 kWの直線とSCR = 3.0の曲線は2つの交点を持ちますが，高め解（青い×印）のみが安定な解であり，低め解（赤い×印）は不安定な解*4となります。この高め解は図4に相当します。すなわち，安定に運転できます。図7では，SCR = 3.0の場合の高め解（青い×印）では，V = 373.14 Vとなっています。図4のLTspiceシミュレーションにおいて，.measコマンドで連系点電圧の実効値*5を確認すると371.66 Vとなっており，概ね一致しています。

また，図7を改めて見ると，SCR = 2.0の場合に，P = 200 kWで臨界状態となるように見えます。そして，それをわずかに下回るSCR = 1.9では，もはやP = 200 kWの直線と交点を持たないため，P = 200 kWでの運転はできません。運転を試みると電圧崩壊に至ることが予想できます。これは図5に相当します。

容量性無効電力を出力した場合のノーズカーブ

図8は，SCRを1.9に固定したまま，受電点でのP + jQの力率角φ = tan⁻¹(Q / P)を変化させた場合のノーズカーブを描いています。

f:id:s-inoue2010:20210728021541p:plain — 図8: SCR = 1.9に固定し，力率角φをパラメータとしたノーズカーブ

力率角φ = 0°の場合は，図7におけるSCR = 1.9の場合とまったく同じ曲線となります。φを変化させていくと，P = 200 kWの曲線との交点を持ちます。例えば，φ = −10°とすると，高め解でV = 367.53 Vとなります。実際にシミュレーションしてみると，図9の波形を得ます。

f:id:s-inoue2010:20210728023055p:plain — 図9: SCR = 1.9，φ = −10°の場合のシミュレーション波形

同じSCR = 1.9ですが，図5とは異なり，電圧崩壊することなく安定運転できていることが判ります。

ノーズカーブから何が言えるか

ノーズカーブでは三相PWM整流器（系統連系自励インバータ）の制御については何も考慮していません。ある意味，理想的な電流制御，電力制御ができているという前提を置いていると言えます。どんなに制御ブロックや制御ゲインを適切に設計しても，ノーズカーブの端点を超えた運転はできません。これは，系統連系自励インバータの運転限界と言えると考えます。逆に，制御ブロックや制御ゲインの設計が不適切である場合，ノーズカーブの端点を超えていなくても，不安定になってしまうと言えそうです。

まとめ

自励インバータの不安定性についての私の理解

私自身，自励インバータでこのような安定性の問題が生じるメカニズムをきちんと理解しておりませんでした。もちろん，系統インピーダンスと電流制御系の相互作用によって自励インバータの運転が不安定になることがあり，これについては本ブログの過去の記事でも取り扱っています*6。しかし，この不安定性が生じるには，その周波数で系統インピーダンスが容量性でなければならず，単に系統が弱い，つまり，誘導性のインピーダンスが大きいだけでは（そのメカニズムの下での）不安定にはなりません。

一方，例えば有効電力制御が働いている三相PWM整流器では，系統電圧が低下した場合，有効電力を指令値通りの一定の値に保とうと，電流を増加させるように反応するはずです。つまり，定電力負荷と言えます。定電力負荷では，電圧が低下すると電流が増加する…要するに，負性抵抗として見えることになります。どう考えても不安定を招きそうな動きですが，有効電力制御を行っているからといって直ちに不安定になるわけではありません。しかし，電力系統工学の教科書からノーズカーブを思い起こすと，定電力負荷は電圧崩壊を招きやすいことが容易に理解できます。ノーズカーブのピーク（ノーズ端）を超え，電圧崩壊を招くか否かは，上位制御のゲイン設計の如何に関わらず，理想的な定電力負荷だとしても，その有効電力のみで決まってしまいます。

そして，上位制御のゲイン設計が不適切である場合，ノーズ端を超えていない段階から振動・発散が起こり，やがてノーズ端を超えて電圧崩壊を招いてしまう──私としては，いまのところこのように理解しています。

なお，無効電力ではなく，交流電圧を制御している場合には，望ましくは自励インバータ自身が自動的に受電点電圧を一定に維持するような無効電流を供給するため，電圧崩壊は起こりにくくなると考えます。しかしこのような場合は，有効電力制御と交流電圧制御のダイナミクスが関係してくるので，小信号モデルを立てた上で安定性を検討するのが良いのかと考えます。つまり，本ブログとしては今後の課題です💧

文献紹介と今後の予定

系統連系自励インバータとSCRの関係について，詳しく研究されるようになってきたのはこの10年ほどではないかと私は推測しています。あらゆる文献を調査した結果という訳ではないのですが，ここでは研究例として，以下の2つを紹介します。

H. Konishi, C. Takahashi, H. Kishibe, and H. Sato, “A consideration of stable operating limits of HVDC system composed of voltage source converters,” IEEJ Trans. IA, vol. 126, no. 4, Apr. 2006, pp. 468-472.
Y. Huang, X. Yuan, J. Hu, and P. Zhou, “Modeling of VSC connected to weak grid for stability analysis of DC-link voltage control,” IEEE J. Emerg. Sel. Topics Power Electron., vol. 3. no. 4, Dec. 2015, pp. 1193-1204.

文献1は，2006年に電気学会産業応用部門誌（D部門誌）で発表された論文であり*7，系統連系電圧形自励インバータと系統のSCRの関係をシミュレーション解析にて探っています*8。有効電力Pと無効電力Qを2次元のマップとして，(P, Q)の組み合わせで安定運転できた場合と不安定になった場合を○，△，×印でプロットしており，例えばSCR= 1.5である場合，P = 1 p.u.として運転するには，Q = −0.6 p.u.（容量性無効電力を負とする）以上を出力する必要があることをシミュレーションにて求めています。

この論文は，自励インバータとSCRの関係に着目した先駆的な研究ではあるものの，安定・不安定の生ずるメカニズムには踏み込んでいません。私としては，これは完全にノーズカーブで説明できるのではないかと考えます。本ブログの本記事は，ある意味でこの論文の追試になっているとも言えると考えます。日本国内では，以後，自励インバータの安定性の研究例は電流制御に関わるものがほとんどであり，上位制御を取り扱った例は見当たりませんでした。

文献2は，2015年にIEEE Journal of Emerging and Selected Topics in Power Electronicsで発表された文献であり，直流電圧制御と連系点電圧制御（いわゆるAC-AVR）が働いている系統連系電圧形自励インバータと系統のSCRやその他パラメータとの関係について，小信号状態空間モデルを立てて解析しています。さらに，固有値解析により，直流電圧制御，PLL (phase-locked loop)，連系点電圧制御のいずれの制御が各振動モードに寄与しているか，刺激係数(participation factor)を求めています。制御ゲインや動作点などにも依存するはずですが，P = 1 p.u.の場合，SCR < 1.2で不安定になるという計算結果（複素平面での固有値の軌跡）を得ており，さらにシミュレーションと実験でも小信号状態空間モデルの妥当性を確認しています。

本ブログでは，文献2を含むいくつかの文献を参考に，私なりに噛み砕いた上で，上位制御と電流制御，PLLを含めた小信号モデルを取り扱うことのできる小信号モデルを立て，LTspiceにてその妥当性を検討してみたいと考えています。

余談

三相PWM整流器（系統連系インバータ）の制御に関する記事だけでは筆者は疲れてしまうので，次回はM5Stack/ESP32を使った簡単な工作のお話でも書いてみようと思っています。

付録: ノーズカーブの導出とPythonプログラム

図6の系統において，有効電力Pと無効電力Qは次式で求められることが知られています。

$P = \displaystyle \frac{E V}{X} \sin \delta \tag{3}$

$Q = \displaystyle \frac{E V \cos \delta - V^{2}}{X} \tag{4}$

この2つの式から，PとVをδと力率角φの関数として計算できる形に書き換えます。

まず，受電点電圧Vの式を作りましょう。力率角をφを用いて

$Q = P \tan \phi \tag{5}$

とおき，(5)式のPとQに(3)，(4)式を代入すると，

$\displaystyle \frac{E V \cos \delta - V^{2}}{X} = \displaystyle \frac{E \cdot V}{X} \sin \delta \tan \phi \tag{6}$

と書くことができます。上式をVについて解くと（えっ？省略？），

$V = \displaystyle \frac{\cos (\delta + \phi)}{\cos \phi} E \tag{7}$

を得ます。

同様に，受電点有効電力Pについての式を作ります。(7)式を(3)式に代入して整理すると，

$P = \displaystyle \frac{E^{2}}{X} \frac{\cos (\delta + \phi) \sin \delta}{\cos \phi} \tag{8}$

を得ます。

(7)式と(8)式では，E，φ，δが分かっていれば，VとPを計算することができます。想定するE，φの下で，δを0°から少しずつ増加させていくと，はじめはPが増加しながらVが変化していき（φ = 0°の場合，Vは低下するのみ），あるδでPが最大値をとり（ノーズカーブの端点），以降はPが減少に転じ，Vは一気に零に向かいます。このようにしてノーズカーブを描くことができます。

本節では，摺り足の加藤さんの「電気の神髄」の下記記事を参考にさせて頂きましたが，記号の使い方や導出された式の形が若干違っていますので，ご了承下さい*9。

Pythonでは，以下のプログラムのようにノーズカーブを描くことができます。

import numpy as np
import matplotlib.pyplot as plt

# 回路定数
E= 400 # [V], 送電端電圧
Pnom = 200e3 # [W], 公称有効電力

# ノーズカーブを計算する関数
def noseCurve(delta, SCR, phi):
    X = E ** 2 / Pnom / SCR # [Ω], リアクタンス
    V = E * np.cos(np.deg2rad(phi + delta)) / np.cos(np.deg2rad(phi))
    P = E ** 2 / X * np.cos(np.deg2rad(delta + phi)) * np.sin(np.deg2rad(delta)) / np.cos(np.deg2rad(phi))
    return V, P

# プロット（力率角をパラメータとする場合）
## SCR
SCR = 1.9 # 固定したSCR
Pop = 200e3 # [W], 運転点

## 準備
fig, ax = plt.subplots(1, 1, figsize = (9, 6))
fig.patch.set_facecolor('lavender')
ax.set_title(f'P-V curve (nose curve) of the 400-V, 200-kW system, fixed SCR = {SCR}')

## 受電端電圧・電力の計算とプロット
delta = np.linspace(0, 180, 180)
phis = [0, -10, -20, -30, -40] # いくつかの短絡容量比
for phi in phis:
    V, P = noseCurve(delta, SCR, phi)
    print(f'phi = {phi}')
    if np.any(P > Pop):
        solution = True
        Vop_h = V[np.min(np.where(P > Pop))]
        Vop_l = V[np.max(np.where(P > Pop))]
        print(f'V = {Vop_h} and {Vop_l} when P = {Pop / 1000} kW') 
    else:
        solution = False
        print(f'P = {Pop} makes voltage collapse!')
    
    ### 特定の力率角でlinewidthを変え，運転点に★印をつける
    if phi in [0, -10]:
        ax.plot(P / 1000, V, label = fr'$\phi = {phi} \degree$', lw = 3)
        if solution == True:
            ax.plot([Pop / 1000], [Vop_h], color = 'blue', ls = '', marker = 'x', ms = 10)
            ax.text(Pop / 1000, E + 175, fr'$\phi = {phi} \degree$, V = {Vop_h:.2f} V', ha = 'center')
            ax.plot([Pop / 1000], [Vop_l], color = 'red', ls = '', marker = 'x', ms = 10)
    else:
        ax.plot(P / 1000, V, label = fr'$\phi = {phi} \degree$', lw = 1)

# 運転点追加
ax.plot([Pop / 1000, Pop / 1000], [0, 600], color = 'blue', ls = '--', lw = 1)

## グラフ調整
ax.set_xlim(0, 400)
ax.set_ylim(0, 600)
ax.set_xlabel('Active power [kW]')
ax.set_ylabel('Receiving-end voltage [V]')
ax.legend(loc = 'lower right')
ax.grid()

上記プログラムを実行すると，本記事の図8を得ます。

*1:本記事では「定格有効電力」としました。定格皮相電力とするなど，考え方は他にもあるのではと考えます。

*2:いや，私自身の中でもこれをきちんと区別できているのか判然としません?? 俺がそう思うんならそうなんだろ。俺ん中ではな…。

*3:本記事ではE = V_nomの場合しか想定していませんが，もちろん背後電圧EがV_nomと異なる値になる場合もあり得ます。

*4:低め解 = 赤い×印の点では，有効電力Pが平衡点から僅かにズレると，そのズレを戻そうとして電流を増減させる作用がさらにPのズレを拡大します。

*5:電流制御（図2）におけるd-q座標系での連系点電圧の絶対値を求めています。

*6:系統連系インバータの電流制御と系統インピーダンス - The Negligible Lab

*7:IPEC-Niigata特集号だったので，英語論文となっているようです。

*8:日本人の研究者・技術者は，この論文のように「解析」という語を無意識に“analysis”と英訳してしまうのですが，方程式の解析解をanalyticalに求めるのではなくシミュレーション解析を主とするのであれば，“simulation study”とか，“numerical experiment”と呼ぶべきではないかと思います。

*9:「電気の神髄」では受電端有効電力Pの式に受電端電圧Vが含まれていますが，本節の(8)式では送電端電圧Eを含む形に導出しました。