数値表現のインピーダンスをα-β座標系からd-q座標系に移す

はじめに

前記事にて三相LCL回路のd-q座標系におけるインピーダンスをHarnefors氏の論文に基づいて（SymPyの力添えを拝借しながら）導出し，LTspiceによる周波数スキャン(frequency response analysis, FRA)の結果と一致することを確認しました。

negligible.hatenablog.com

その際，今後の議論として以下のような宿題が残りました。

もし，（静止座標系でのインピーダンスである）Z^s(s)のトポロジーや回路定数が分からず，したがって数式表現が未知であり，例えばインピーダンスアナライザでの測定結果のようにZ^s(jω)の数値データだけが手元にあった場合，これを使ってd-q座標系でのインピーダンスZ_d(jω)，Z_q(jω)を（近似でもよいので）得ることはできるでしょうか？

前記事を書き終えた時点では，「Z^s(jω)の数値データからシステム同定の手法にてZ^s(s)の数式表現を推定するしかないのではないか」と考えておりました。とは言え，筆者自身でもZ^s(s + jω)をZ^s(s)の周りでテイラー展開してみたりと試行錯誤を繰り返していました。

そんな中，ノルウェー科学技術大学(Norges teknisk-naturvitenskapelige universitet, NTNU)のAtle Rygg氏の学位論文（下記リンク参照。以下，「Rygg氏の学位論文」と呼びます）において，d-q座標系，修正対称座標系(modified sequence domain)，従来の対称座標系で表現したインピーダンスの間の関係が整理されており，それらの間の座標変換について，簡潔にまとまられていることを見つけました。

ntnuopen.ntnu.no

https://www.researchgate.net/publication/328231490_Impedance-based_methods_for_small-signal_analysis_of_systems_dominated_by_power_electronics

これを用いればZ^s(jω)の数値データからd-q座標系でのインピーダンスZ_d(jω)，Z_q(jω)を簡便に計算できることが分かりました。前記事にて取り扱った三相LCL回路に適用してみましたので，本記事にて紹介致します。

また，筆者なりにHarnefors氏の論文とRygg氏の学位論文の比較考察をしてみましたので，馬鹿げた記述かもしれませんが一応書いておきます。

結論

まず結論をざっと示します。静止(α-β)座標系でのインピーダンスがZ^s(s)である場合（三相平衡を仮定します。また上付きsはstationary = 静止座標系を意味します），Harnefors氏の論文に基づいてd-q座標系に移す場合，

$\begin{align} Z_{d}(s) &= \mathrm{Re} \left [ Z^{s}(s + j \omega_{1}) \right ] \\[10pt] Z_{q}(s) &= \mathrm{Im} \left [ Z^{s}(s + j \omega_{1}) \right ] \end{align} \tag{1}$

と計算することができます。d軸とq軸にインピーダンスを分けるには，(1)式右辺のZ^s(s + jω₁)の実部と虚部を（ラプラス演算子sはひとまず実数と見なして）計算する必要があります。しかし，もともとのZ^s(s)の数式表現が手元になく，周波数伝達関数としてのZ^s(jω)の数値データしか入手できない場合，(1)式に相当する計算は難しそうに見えます。

しかし，Rygg氏の学位論文によれば，何とZ^s(jω)から

$\begin{align} Z_d(j \omega) &= \frac{Z^{s}(j (\omega + \omega_{1})) + Z^{s}(j (\omega - \omega_{1}))}{2} \\[10pt] Z_q(j \omega) &= \frac{Z^{s}(j (\omega + \omega_{1})) - Z^{s}(j (\omega - \omega_{1}))}{2j} \end{align} \tag{2}$

のように簡単に計算することができます。そう，Z^s(jω)の周波数をω₁だけ両方向にシフトしたものを作り，その和を2で除したもの（つまり平均）がd軸成分，その差を2jで除したものがq軸成分となります。以下，実際にやってみましょう。

各インピーダンスの関係

ここではRygg氏の学位論文に記載されているインピーダンスの変換について概観します。

対称座標系でのインピーダンス

三相システムにおける対称座標系については広く知られていることですが，例えば各相の電圧V_a(jω)，V_b(jω)，V_c(jω)から零相電圧V₀(jω)，正相電圧V_p(jω)，逆相電圧V_n(jω)へは次式のように変換します。

$\begin{bmatrix} V_{0}(j \omega) \\ V_{p}(j \omega) \\ V_{n}(j \omega) \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 1 & a & a^{2} \\ 1 & a^{2} & a \end{bmatrix} \begin{bmatrix} V_{a}(j \omega) \\ V_{b}(j \omega) \\ V_{c}(j \omega) \end{bmatrix},\quad (a = e^{j \frac{2 \pi}{3}}) \tag{3}$

同様の変換は電流についても成立します。インピーダンスが三相平衡であり，正相成分と逆相成分の干渉がない場合，正相回路と逆相回路は独立となり，それぞれのインピーダンスをZ_p(jω)，Z_n(jω)とすれば，

$Z_{p}(j \omega) = \displaystyle \frac{V_{p}(j \omega)}{I_{p}(j \omega)}, \quad Z_{n}(j \omega) = \displaystyle \frac{V_{n}(j \omega)}{I_{n}(j \omega)} \tag{4}$

と書けます。

修正対称座標系でのインピーダンス

Rygg氏の学位論文は修正対称座標系と呼ばれる次式のような表現方法を導入しています。

$\begin{bmatrix} V_{p}(s + j \omega_{1}) \\ V_{n}(s - j \omega_{1}) \end{bmatrix} = \underbrace{\begin{bmatrix} Z_{pp}(s) & Z_{pn}(s) \\ Z_{np}(s) & Z_{nn}(s) \end{bmatrix}}_{\displaystyle \boldsymbol{Z}_{pn}(s)} \begin{bmatrix} I_{p}(s + j \omega_{1}) \\ I_{n}(s - j \omega_{1}) \end{bmatrix} \tag{5}$

(5)式は周波数伝達関数として

$\begin{bmatrix} V_{p}(j (\omega + \omega_{1})) \\ V_{n}(j (\omega - \omega_{1})) \end{bmatrix} = \underbrace{\begin{bmatrix} Z_{pp}(j \omega) & Z_{pn}(j \omega) \\ Z_{np}(j \omega) & Z_{nn}(j \omega) \end{bmatrix}}_{\displaystyle \boldsymbol{Z}_{pn}(j \omega)} \begin{bmatrix} I_{p}(j (\omega + \omega_{1})) \\ I_{n}(j (\omega - \omega_{1})) \end{bmatrix} \tag{6}$

と書くこともできます。(5)式のZ_pn(s)の非対角成分Z_pn(s)とZ_np(s)は異なる周波数成分の間のカップリングを表現しています。Rygg氏の学位論文ではこれをmirror frequency coupling*1と称しています。正相成分と逆相成分のカップリングがない場合，Z_pn(s) = Z_np(s) = 0となり，Z_pn(s)は対角成分のみとなります。この場合，

$\begin{bmatrix} V_{p}(j (\omega + \omega_{1})) \\ V_{n}(j (\omega - \omega_{1})) \end{bmatrix} = \underbrace{\begin{bmatrix} Z_{pp}(j \omega) & 0 \\ 0 & Z_{nn}(j \omega) \end{bmatrix}}_{\displaystyle \boldsymbol{Z}_{pn}(j \omega)} \begin{bmatrix} I_{p}(j (\omega + \omega_{1})) \\ I_{n}(j (\omega - \omega_{1})) \end{bmatrix} \tag{7}$

と書くことができます。Rygg氏の学位論文ではこのような系をmirror frequency decoupled (MFD)と称しています。三相平衡である場合，MFDになります。

修正対称座標系とd-q座標系の関係

d-q座標系での電圧，電流，インピーダンスは次式のように表現できるとします*2。

$\begin{bmatrix} V_{d}(s) \\ V_{q}(s) \end{bmatrix} = \underbrace{\begin{bmatrix} Z_{dd}(s) & Z_{dq}(s) \\ Z_{qd}(s) & Z_{qq}(s) \end{bmatrix}}_{\displaystyle \boldsymbol{Z}_{dq}(s)} \begin{bmatrix} I_{d}(s) \\ I_{q}(s) \end{bmatrix} \tag{8}$

ここで，MFDな系である場合，Z_dq(s)の対角成分は等しく，非対角成分は大きさが等しく逆符号となります。すなわち，

$\begin{bmatrix} V_{d}(s) \\ V_{q}(s) \end{bmatrix} = \underbrace{\begin{bmatrix} Z_{d}(s) & -Z_{q}(s) \\ Z_{q}(s) & Z_{d}(s) \end{bmatrix}}_{\displaystyle \boldsymbol{Z}_{dq}(s)} \begin{bmatrix} I_{d}(s) \\ I_{q}(s) \end{bmatrix} \tag{9}$

となります*3。

さて，Rygg氏の学位論文には，修正対称座標系とd-q座標系の間で，電圧・電流は次式のように変換できると記載があります。

$\begin{align} \begin{bmatrix} V_{p}(s + j \omega_{1}) \\ V_{n}(s - j \omega_{1}) \end{bmatrix} &= \displaystyle \frac{1}{\sqrt{6}} \begin{bmatrix} 1 & j \\ 1 & -j \end{bmatrix} \begin{bmatrix} V_{d}(s) \\ V_{q}(s) \end{bmatrix} \\[10pt] \begin{bmatrix} I_{p}(s + j \omega_{1}) \\ I_{n}(s - j \omega_{1}) \end{bmatrix} &= \displaystyle \frac{1}{\sqrt{6}} \begin{bmatrix} 1 & j \\ 1 & -j \end{bmatrix} \begin{bmatrix} I_{d}(s) \\ I_{q}(s) \end{bmatrix} \end{align} \tag{10}$

(10)式を(5)式に代入すれば，

$\displaystyle \frac{1}{\sqrt{6}} \begin{bmatrix} 1 & j \\ 1 & -j \end{bmatrix} \begin{bmatrix} V_{d}(s) \\ V_{q}(s) \end{bmatrix} = \boldsymbol{Z}_{pn}(s) \displaystyle \frac{1}{\sqrt{6}} \begin{bmatrix} 1 & j \\ 1 & -j \end{bmatrix} \begin{bmatrix} I_{d}(s) \\ I_{q}(s) \end{bmatrix} \tag{11}$

となり，さらに両辺に左から

$\left ( \displaystyle \frac{1}{\sqrt{6}} \begin{bmatrix} 1 & j \\ 1 & -j \end{bmatrix} \right )^{-1} \tag{12}$

を掛ければ，

$\begin{bmatrix} V_{d}(s) \\ V_{q}(s) \end{bmatrix} = \underbrace{\begin{bmatrix} 1 & j \\ 1 & -j \end{bmatrix}^{-1} \boldsymbol{Z}_{pn}(s) \begin{bmatrix} 1 & j \\ 1 & -j \end{bmatrix}}_{\displaystyle \boldsymbol{Z}_{dq}(s)} \begin{bmatrix} I_{d}(s) \\ I_{q}(s) \end{bmatrix} \tag{13}$

となります。以上より，変換行列A_Zがユニタリ行列になるようにうまく係数をかけると，Z_dq(s)とZ_pn(s)の変換は次式のように書けます。

$\begin{align} \boldsymbol{Z}_{dq}(s) &= A_{Z}^{-1} \boldsymbol{Z}_{pn}(s) A_{Z} \\[10pt] \boldsymbol{Z}_{pn}(s) &= A_{Z} \boldsymbol{Z}_{dq}(s) A_{Z}^{-1} \end{align} \tag{14}$

ただし，

$A_{Z} = \displaystyle \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & j \\ 1 & -j \end{bmatrix} \tag{15}$

です。

修正対称座標系とα-β座標系の関係

三相平衡な場合，静止(α-β)座標系では，

$\begin{bmatrix} V_{\alpha}(s) \\ V_{\beta}(s) \end{bmatrix} = \begin{bmatrix} Z^{s}(s) & 0 \\ 0 & Z^{s}(s) \end{bmatrix} \begin{bmatrix} I_{\alpha}(s) \\ I_{\beta}(s) \end{bmatrix} \tag{16}$

です。修正対称座標系では，(5)式の通り，周波数がs + jω₁，s − jω₁である場合のインピーダンスZ_pp(s)，Z_nn(s)を考えるため，α-β座標系でのインピーダンスZ^s(s)の周波数をシフトすればよいと言えます。すなわち，

$\begin{align} Z_{pp}(s) &= Z^{s}(s + j \omega_{1}) \\[10pt] Z_{nn}(s) &= Z^{s}(s - j \omega_{1}) \end{align} \tag{17}$

となり，周波数伝達関数としては，

$\begin{align} Z_{pp}(j \omega) &= Z^{s}(j (\omega + \omega_{1})) \\[10pt] Z_{nn}(j \omega) &= Z^{s}(j (\omega - \omega_{1})) \end{align} \tag{18}$

と書けます。また，三相平衡の場合，Z_pn(jω) = Z_np(jω) = 0です。(18)式を(14)式に代入して整理すると，

を得ます（これは(2)式の再掲です）。

計算例

(19)式はZ^s(jω)の数値データがあれば，横軸（周波数）をシフトさせるだけで計算できそうです。そこで，前記事で取り扱った三相LCL回路を例に計算してみました。図1，2に計算例を示します。

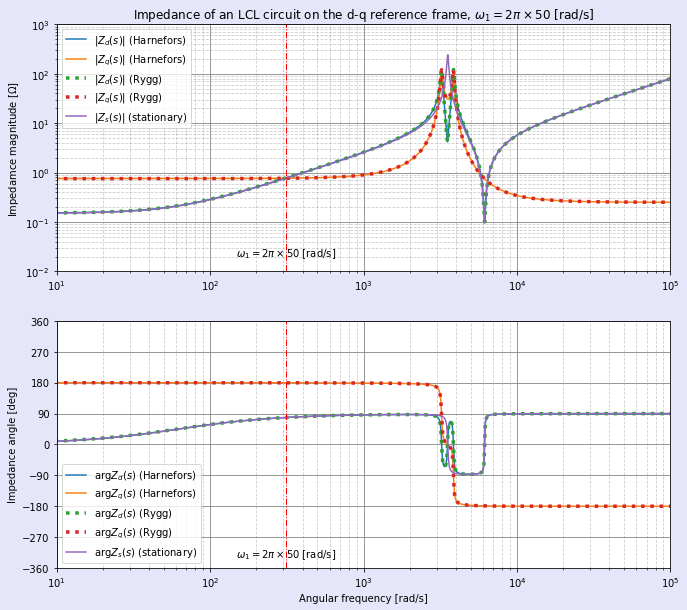
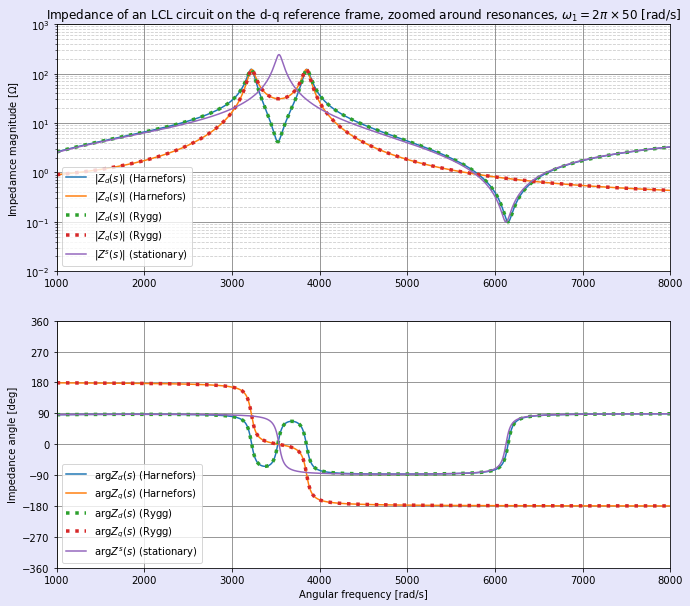
図2: 三相LCL回路のd-q座標系でのインピーダンス計算例（共振周波数付近拡大）

前記事にてHarnefors氏の論文に基づいてSymPy-NumPyの合わせ技でanalyticalに計算した結果と，本記事にてRygg氏の学位論文に基づいて(19)式からnumericalに計算した結果が，見事に一致することが確認できます。

2つの方法の比較考察

以下，筆者としていろいろ考えてみた結果を書き散らしています。

Harnefors氏の表現とRygg氏の表現

さて，2つの異なる表現が同じ結果を与えました。Harnefors氏の表現とRygg氏の表現は等しいはずなので，

$\begin{align} \mathrm{Re} \left [ Z^{s}(s + j \omega_{1}) \right ] &= \frac{Z^{s}(s + j \omega_{1}) + Z^{s}(s - j \omega_{1})}{2} \\[10pt] \mathrm{Im} \left [ Z^{s}(s + j \omega_{1}) \right ] &= \frac{Z^{s}(s + j \omega_{1}) - Z^{s}(s - j \omega_{1})}{2j} \end{align} \tag{20}$

が成り立っているはずです。(20)式を見ると，どことなくコサインとサインの指数関数表記

$\begin{align} \cos \theta = \frac{e^{j \theta} + e^{-j \theta}}{2} \\[10pt] \sin \theta = \frac{e^{j \theta} - e^{-j \theta}}{2j} \end{align} \tag{21}$

にも似ています。むむッ！これって「テイラー展開してみなはれ」という天の思し召しではありませんか？

テイラー展開してみる

という訳で，(20)式右辺に登場するZ^s(s + jω)とZ^s(s − jω)をsの周りでテイラー展開してみましょう*4。

$\begin{align} Z^{s}(s + j \omega_{1}) &= \displaystyle Z^{s}(s) + \frac{d Z^{s}(s)}{ds} \frac{j \omega_{1}}{1!} + \frac{d^{2} Z^{s}(s)}{ds^{2}} \frac{(j \omega_{1})^{2}}{2!} \\[10pt] &+ \frac{d^{3} Z^{s}(s)}{ds^{3}} \frac{(j \omega_{1})^{3}}{3!} + \frac{d^{4} Z^{s}(s)}{ds^{4}} \frac{(j \omega_{1})^{4}}{4!} + \dots \end{align} \tag{22}$

$\begin{align} Z^{s}(s - j \omega_{1}) &= \displaystyle Z^{s}(s) + \frac{d Z^{s}(s)}{ds} \frac{-j \omega_{1}}{1!} + \frac{d^{2} Z^{s}(s)}{ds^{2}} \frac{(-j \omega_{1})^{2}}{2!} \\[10pt] &+ \frac{d^{3} Z^{s}(s)}{ds^{3}} \frac{(-j \omega_{1})^{3}}{3!} + \frac{d^{4} Z^{s}(s)}{ds^{4}} \frac{(-j \omega_{1})^{4}}{4!} + \dots \end{align} \tag{23}$

(22)，(23)式の右辺を見ると，jω₁の偶数次の項は実数に，奇数次の項は虚数になることが分かります。 (22)式と(23)式を辺々加えて2で割ると，それぞれの右辺の奇数次の項がキャンセルするため，

$\begin{align} \displaystyle \frac{Z^{s}(s + j \omega_{1}) + Z^{s}(s - j \omega_{1})}{2} &= Z^{s}(s) - \frac{d^{2} Z^{s}(s)}{ds^{2}} \frac{\omega_{1}^{2}}{2!} \\[10pt] &+ \frac{d^{4} Z^{s}(s)}{ds^{4}} \frac{\omega_{1}^{4}}{4!} - \frac{d^{6} Z^{s}(s)}{ds^{6}} \frac{\omega_{1}^{6}}{6!} + \dots \end{align} \tag{24}$

となります。また，(22)式から(23)式を辺々引いて2jで割ると，それぞれの右辺の偶数次の項がキャンセルするため，

$\begin{align} \displaystyle \frac{Z^{s}(s + j \omega_{1}) - Z^{s}(s - j \omega_{1})}{2j} &= \frac{d Z^{s}(s)}{ds} \frac{\omega_{1}}{1!} + \\[10pt] &- \frac{d^{3} Z^{s}(s)}{ds^{3}} \frac{\omega_{1}^{3}}{3!} + \frac{d^{5} Z^{s}(s)}{ds^{5}} \frac{\omega_{1}^{5}}{5!} - \dots \end{align} \tag{25}$

と書けます。

ところで，(22)式を実部と虚部に分けることができれば，すなわちHarnefors氏の論文におけるZ_d(s)とZ_q(s)に分けることができると言えます。(22)式の右辺を見ると分かる通り，偶数次の項が実数に，奇数次の項が虚数となります。実際に分けてみると，

$\begin{align} \mathrm{Re} \left [ Z^{s}(s + j \omega_{1}) \right ] &= Z^{s}(s) - \frac{d^{2} Z^{s}(s)}{ds^{2}} \frac{\omega_{1}^{2}}{2!} \\[10pt] &+ \frac{d^{4} Z^{s}(s)}{ds^{4}} \frac{\omega_{1}^{4}}{4!} - \frac{d^{6} Z^{s}(s)}{ds^{6}} \frac{\omega_{1}^{6}}{6!} + \dots \end{align} \tag{26}$

$\begin{align} \mathrm{Im} \left [ Z^{s}(s + j \omega_{1}) \right ] &= \frac{d Z^{s}(s)}{ds} \frac{\omega_{1}}{1!} + \\[10pt] &- \frac{d^{3} Z^{s}(s)}{ds^{3}} \frac{\omega_{1}^{3}}{3!} + \frac{d^{5} Z^{s}(s)}{ds^{5}} \frac{\omega_{1}^{5}}{5!} - \dots \end{align} \tag{27}$

を得ます。項毎に比較してみると，(26)，(27)式右辺はそれぞれ(24)，(25)式右辺と等しいことが分かります。すなわち，(20)式が成り立っています。当初筆者は，無限に続いていく(26)，(27)式の項を途中で打ち切れば近似できるのではないかとして，Z^s(jω)をjωで何度も微分したりと試行錯誤をしていましたが*5，そのような無限の項を扱うことなく，実部と虚部に簡単に分けることができるというのは大変に不思議です。

数学的に厳密かどうかまったく自信がありませんが，筆者としては，Harnefors氏の論文における表現と，Rygg氏の学位論文における表現は等しいと言えるのではないかと考えます。

LTspiceでの波形の観察

さて，(19)式についてはLTspiceでの波形を見ると，自ずと導き出された可能性があります。図3に三相LCL回路のLTspiceスキマティックを示します。

図3は前記事にてFRAを実施した際に使用した回路ですが，今回はd-q座標系において，

$\begin{align} v_{d}(t) &= \cos \omega t~[\mathrm{V}], \quad (\omega = 2 \pi \times 70~[\mathrm{rad/s}]) \\[10pt] v_{q}(t) &= 0~[\mathrm{V}] \end{align}\tag{28}$

フェーザ表現で，

$\begin{align} V_{d}(j \omega) &= 1 \times e^{j 0} = 1~[\mathrm{V}] \\[10pt] V_{q}(j \omega) &= 0~[\mathrm{V}] \end{align} \tag{29}$

とした場合の挙動の波形を詳しく見てみます。

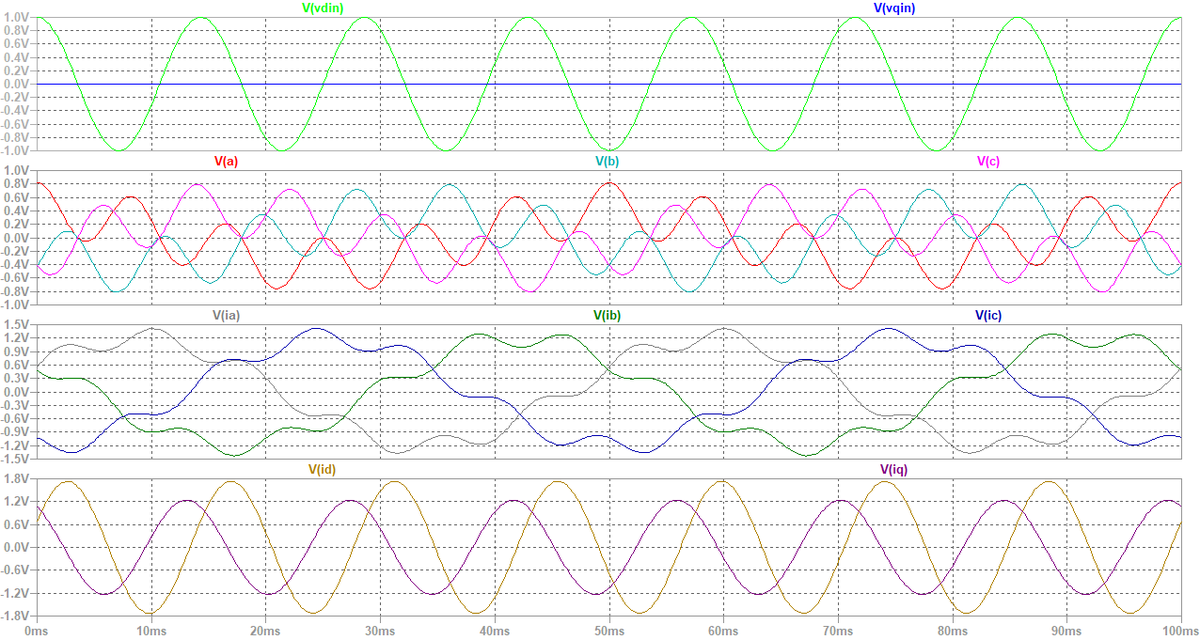
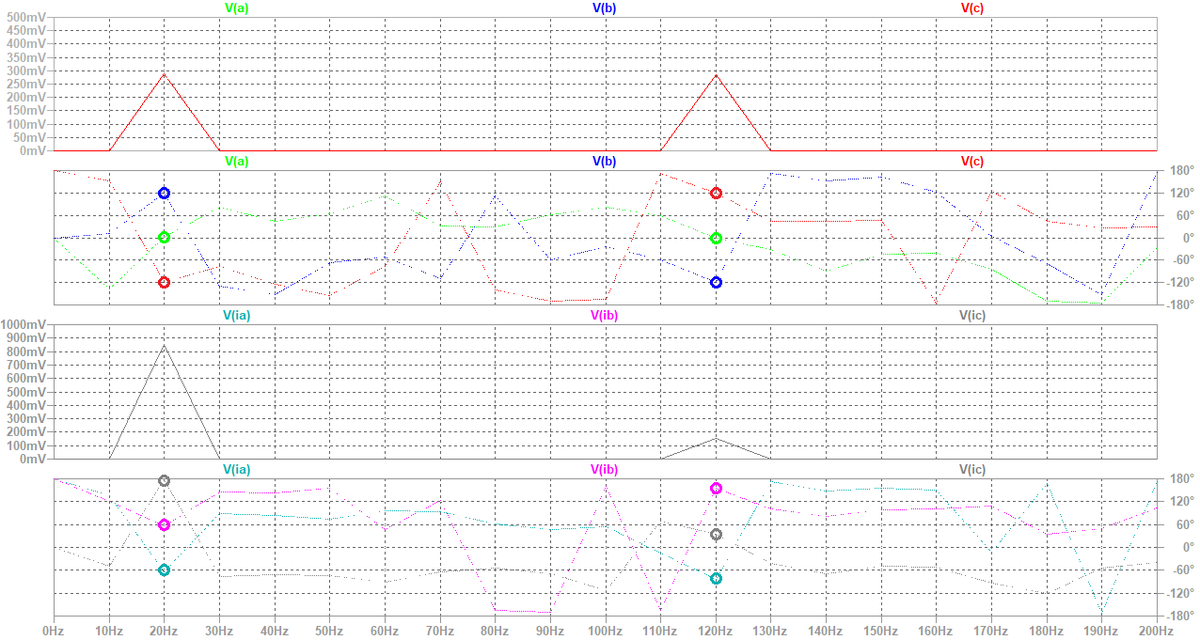
図4にシミュレーション波形を示します。また，図5に，三相座標系での電圧v(a), v(b), v(c)および電流ia, ib, ic（電圧信号となるので図5ではv(ia), v(ib), v(ic)と表記されています）のスペクトルを示します。また，図6にd-q座標系での時間波形，d-q座標系でのベクトル図，α-β座標系でのベクトル図の関係を筆者なりに考察した図を示します。以下の説明で図6を適宜参照します。

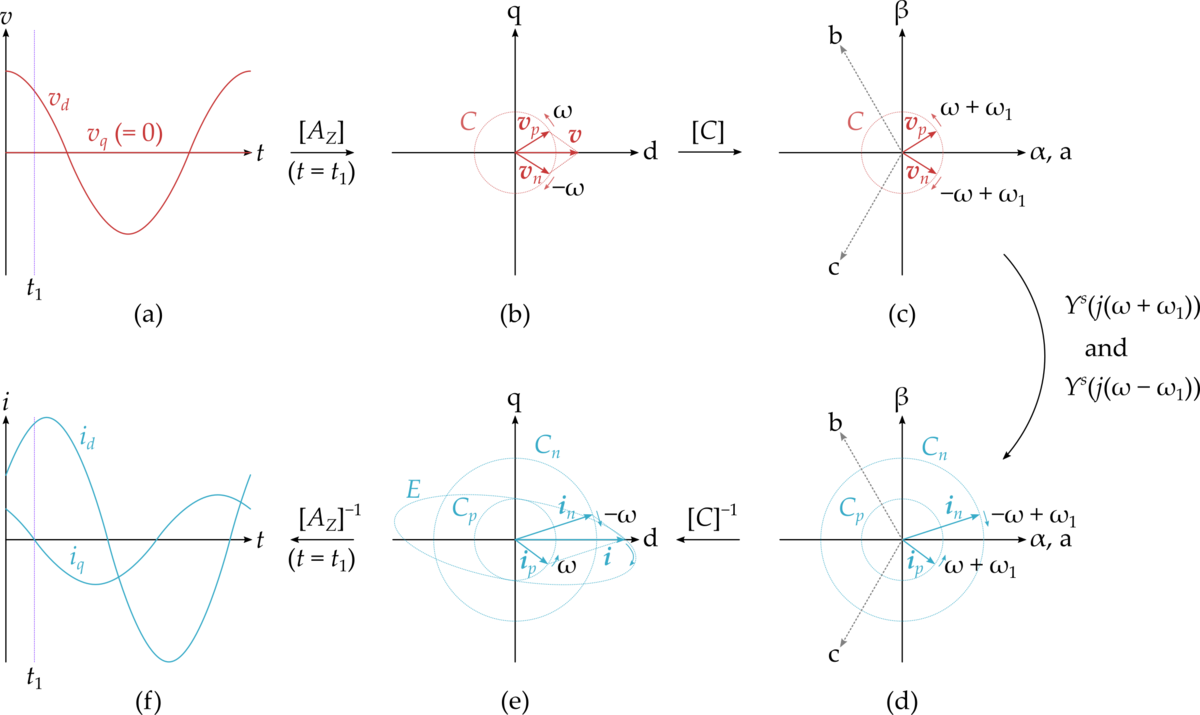
(28)式および図6(a)の通り，d軸電圧を振幅1 V，周波数70 Hzの正弦波*6とし，q軸電圧を零としています。これをd-q座標系のベクトル図としてプロットすると，図6(b)のように正相成分v_p，逆相成分v_nの重ね合わせとみることができます。v_pとv_nのq軸成分が打ち消しあうので，電圧ベクトルvはd軸成分のみを持つことになります。

d-q逆変換，α-β逆変換の後に得られる三相座標系での電圧v(a), v(b), v(c)を図4で確認すると，正弦波にはなっていないことが分かります。また，各相で電圧波形が異なることも分かります（ピーク付近を見比べると，山の位置が相毎に異なります）。図5に示すように，LTspiceのFFT機能を使ってスペクトルを分析してみると，v(a), v(b), v(c)には入力した70 Hzとd-q座標系の回転周波数50 Hzの和120 Hzと差20 Hzの成分が含まれていることが判ります。2つの成分の振幅は同じです。これは，図6(c)に示すように，α-β座標系ではv_pとv_nの周波数がω + ω₁ (120 Hz)とω − ω₁ (20 Hz)に割れてしまうためです。また，図5を見ると，v(a), v(b), v(c)の120 Hz成分の相順はa, b, cとなっており正相成分，20 Hz成分の相順はa, c, bとなっており逆相であることが判ります。

当然ながら三相LCL回路のアドミタンスはω + ω₁ (120 Hz)とω − ω₁ (20 Hz)で異なるので，図6(d)に示すように，流れる電流ia, ib, icの120 Hz成分と20 Hz成分の振幅や位相は異なります。なお，三相LCL回路が三相平衡であれば，正相120 Hzの電圧を印加されれば電流も正相120 Hz，逆相20 Hzの電圧を印加されれば電流も逆相20 Hzとなります。本記事では取り扱いませんでしたが，不平衡であれば，正相と逆相のカップリングが起きるはずです。また，線形回路であるため，120 Hzでも20 Hzでもない第3の周波数成分が生まれたりはしません。結果として，今回の回路パラメータや70 Hzという入力周波数の下では，図5の3，4段目のように20 Hz成分が卓越する形となります。

これをα-β変換，d-q変換して再びd-q座標系に戻すと，図6(e)に示すように，正相成分の120 Hz成分は50 Hzが減じられて70 Hzに，逆相成分の20 Hzは50 Hzが加えられて同じく70 Hzに戻ってきます。正相電流ベクトルi_pと逆相電流ベクトルi_nを合成した電流ベクトルiの先端は楕円を描きます。これを時間波形として描けば図6(f)となり，シミュレーション波形としては図4の最下段になります。

このように，静止座標系でのインピーダンスを回転(d-q)座標系に移そうとすると，必然的に正相・逆相成分に分けて考える必要があり，しかもそれぞれが静止(α-β)座標系でω + ω₁ (120 Hz)とω − ω₁ (20 Hz)という異なる周波数に変換されることから，(19)式のようにそれぞれのインピーダンスの和や差として導出されると定性的には理解することができます。

まとめ

本記事では，静止(α-β)座標系でのインピーダンスZ^s(jω)の数値データから回転(d-q)座標系でのインピーダンスZ_d(jω)，Z_q(jω)を簡便に計算する方法を，Rygg氏の学位論文を紹介しながら説明しました。また，Harnefors氏の論文に記載されている数式との関係をテイラー展開を用いて（誤っているかもしれませんが）考察してみました。

さらに，LTspiceを用いたシミュレーション波形から，回転(d-q)座標系から見たインピーダンスは，静止(α-β)座標系における2つの周波数におけるインピーダンスから導かれることを考察しました。

基本波正相成分を直流に見せようと願った分，他の周波数成分を2つに割らずにはいられない…。 d-q座標系ってそういう仕組みだったんだね…。あたしって，ほんとバカ…。

何と言うか，d-q変換を使った系統連系変換器の制御にこれまで長く親しんできましたが，つい最近までこのような考えに至ることができず，不勉強を恥じてばかりです。

さて，前記事の最後にも書きましたが，今後はパッシブなインピーダンスの方ではなく，三相系統連系変換器の制御系を含めたインピーダンスについて，同じくRygg氏の学位論文やHarnefors氏の論文，また，F. Blaabjerg先生の論文や教科書を参考にしながら勉強していきたいと思っています*7。

付録: Pythonでの計算方法について

本記事のグラフ（図1，2）を計算した際に書いたJupyter NotebookをGitHubに置きました*8。

github.com

Rygg氏の学位論文に基づいて(19)式の計算を行うにあたって，ひとつ工夫したところがあります。往々にして，広い周波数範囲のインピーダンスをデータ化しようとした場合，周波数軸は対数にする（片対数グラフとする）のが一般的かと思われます。その状態で，±ω₁ = ±2 π × 50 [rad/s]だけ周波数をシフトしようとした場合，つまりZ^s(jω)のデータからZ^s(j(ω ± ω₁))を得ようとした場合，ちょうどその周波数でのデータが存在しないことが予期されます（特に50 Hzや60 Hzが相対的に小さく見える高周波領域）。そこで，

from scipy import interpolate

## ±jω1を自由に足し引きできるように線形補完を定義する
Zs_interp = interpolate.interp1d(_omega, Zs_bode, fill_value = 'extrapolate')

## 周波数をシフトしてインピーダンスの対角・非対角成分を計算する
Zd_rygg = (Zs_interp(_omega + _omega1) + Zs_interp(_omega - _omega1)) / 2
Zq_rygg = (Zs_interp(_omega + _omega1) - Zs_interp(_omega - _omega1)) / 2j

のように，scipy.intepolate.interp1d関数を用いて，元のZ^s(jω)すなわちZs_bodeを線形補間するようにしました。図1，2は上のZd_ryggとZq_ryggを_omegaに対してプロットしたものです。

*1:Mirror frequency coupling = 鏡像周波数カップリングとでも訳しましょうか。

*2:Harnefors氏の論文とRygg氏の学位論文では非対角成分の添え字の付け方が逆になっています。(8)式ではRygg氏の書き方に従います。

*3:Harnefors氏の論文では対角成分をZ_d(s)，非対角成分を±Z_q(s)と表記していますが，Rygg氏の学位論文ではそれぞれZ_diag(s)，±Z_offdiag(s)と表記しています。(9)式では前記事に合わせてHarnefors氏の表記方法に従います。

*4:sはラプラス演算子ですが，そのsの周りでのテイラー展開などと言うものができるのかどうか，筆者は残念ながら知りません…💧

*5:

三相LCL回路の静止座標系におけるインピーダンスZs(jω)の数値データから回転座標系におけるZd(jω)とZq(jω)を得る試み…。
どうもダメっぽい💧
いったん頭を冷やそう😅 pic.twitter.com/WcOOMoqyvb
— RR-いにょ (@RR_Inyo) 2021年5月6日

*6:コサインなので厳密には「余弦波」と呼ぶべき？広義にはコサインも「正弦波」に入ると思っていますが…。

*7:このところNucleoやRaspberry Piに触っていないので，再びプログラミングや電子工作でも遊んでみたいという気もしています…💧

*8:GitHub上で観ると，Markdownセルの数式が崩れてしまいます。

The Negligible Lab

Astray in the forest of electrical and electronic circuits. Adrift in the gap between time and frequency domains. 独立独歩を是とする。