Pythonによる台車形倒立振子の線形化と最適レギュレータ

はじめに

P計画: 倒立振子の思ひ出

筆者のメインPCは11年物のSandy Bridge (Intel Core i7-2600K)を使用した骨董品です。そのHDDの奥底から，はるか昔の実験レポートが出土しました*1。今でも図1のようにMicrosoft Wordで開くことができます。

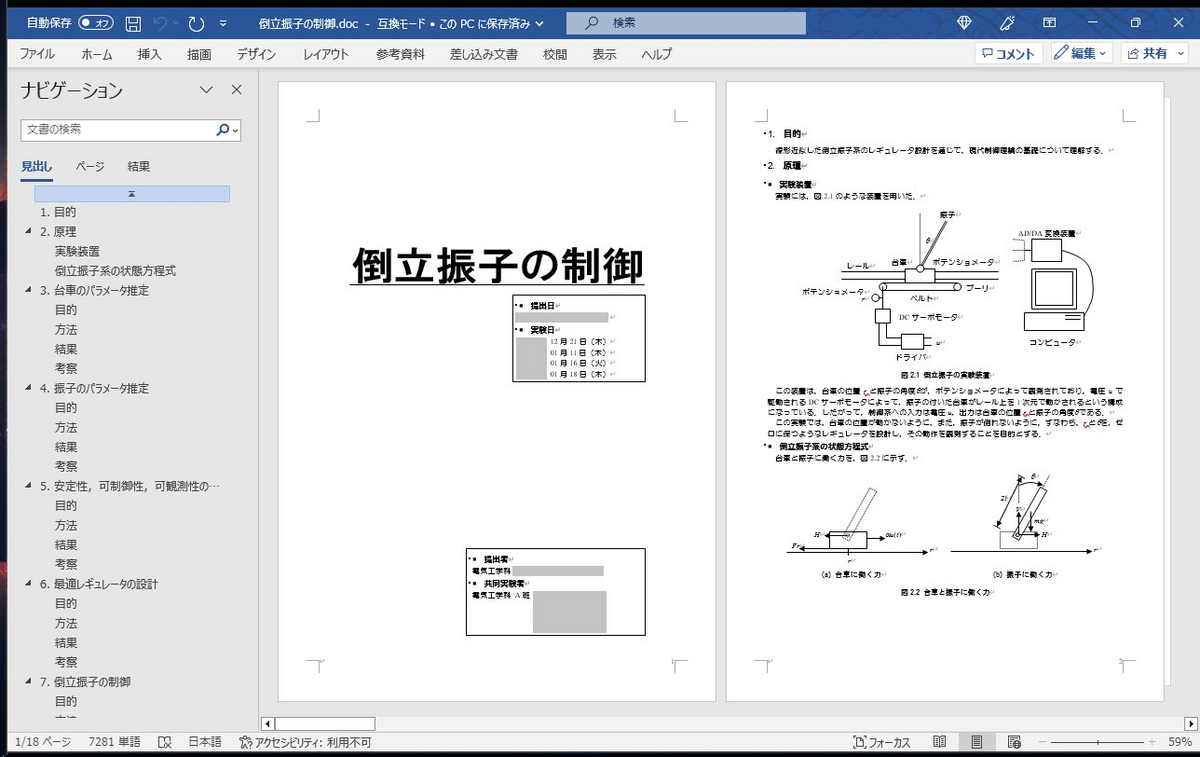
そう，筆者は過去に台車形倒立振子を触ったことがあったのでした。読み返してみると，非線形な運動方程式としてのシミュレーションはしておらず，ほぼいきなり線形化したモデルから始まっていました。ベルト駆動の台車をガタガタさせながら，鉄の棒を倒立させていたことを懐かしく思い出します。

完成イメージ

さて，前回を簡単に振り返りますと，車輪形倒立振子を設計・製作する前段階として，Pythonによる台車形倒立振子のシミュレーションを試みたのでした。具体的には台車形倒立振子の運動方程式（を基にした非線形状態方程式）を導出し，SciPyのsolve_ivp関数にて初期値問題を解き，Matplotlibにてアニメーションとして可視化しています。

本記事では，前回導出した非線形状態方程式を線形化して状態空間モデルを立て，アニメーションを作成します。

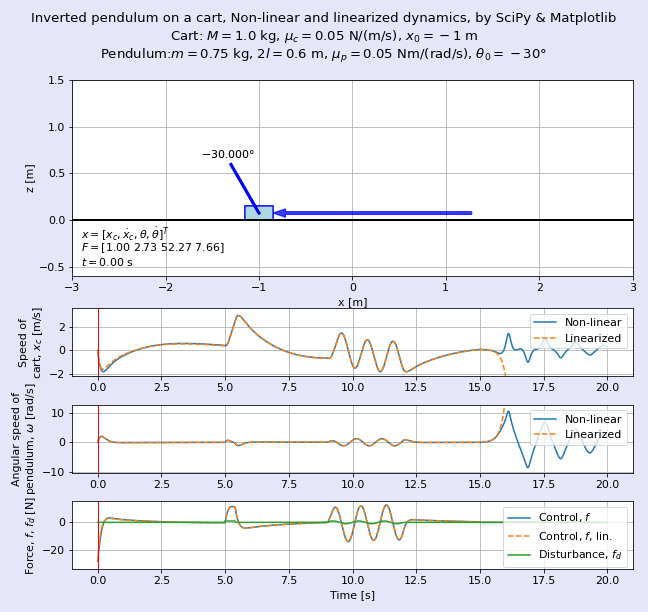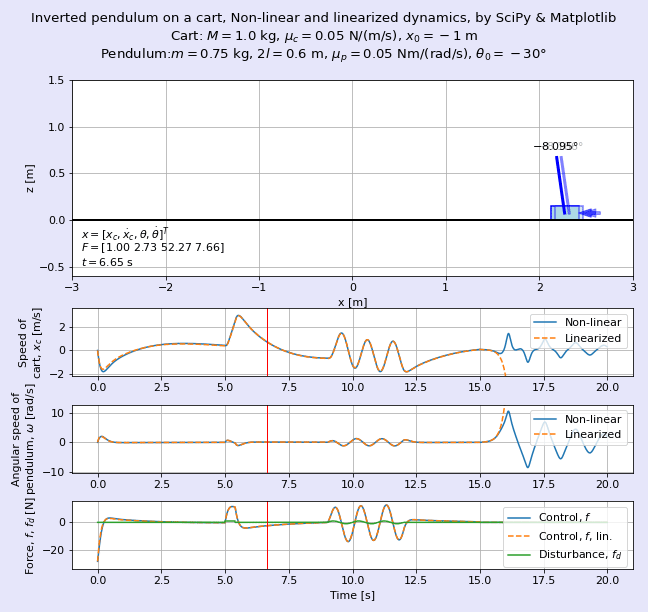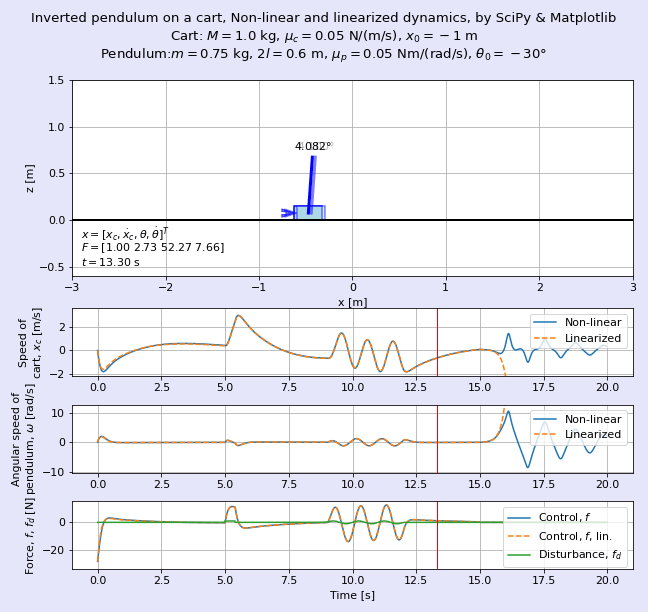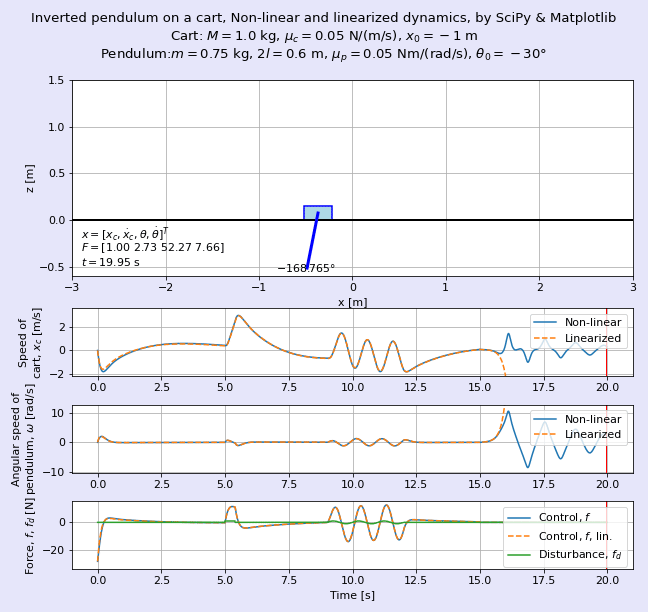
完成イメージとして，図2に非線形な系である台車形倒立振子とその線形化モデルの挙動を重ねて表示したアニメーションを示します。よく見るとゴーストのように薄い色の台車と振り子がほぼ重なって動いていますが，この色が薄い方が線形化モデルです。

筆者として長らく疑問であった点であり，また，制御工学に関する種々の教科書でもあまり言及されていない*2話題として，「線形化したモデルは，元の非線形なシステムのふるまいをどれだけ近似していると言えるのか」という問いがありました。図2のアニメーションは，台車形倒立振子について元の非線形な状態方程式と，それを線形化した状態空間モデルのふるまいを重ねて表示し，筆者の感覚的な理解の促進を狙ったものです。

図2では時刻t = 15 s以降で制御を止めているため，非線形な元の倒立振子は下向きに倒れてブラブラと揺れますが，線形化した倒立振子は高速回転しながらはるか彼方へふっ飛んでいきます。吉田勝俊先生の「短期集中：振動論と制御理論」（日本評論社，2003年）のp. 71の脚注にある通り，「線形化してしまったので，回転しないで発散する」を体現していますね。

本記事ではまた，SciPyのlinalg.solve_continuous_are関数を使って線形化した状態空間モデルに関するRiccati方程式を解き，最適レギュレータ(LQR, linear quadratic regulator)の設計を試みます。

いずれにしても本記事は筆者個人としての現代制御理論の初歩の学び直しのための備忘録のようなものであり，学術的に何ら新規性のある記述はしていませんのでご了承下さい。

図2を生成するJupyter NotebookをGitHubに起きましたので，適宜ご参照下さい。

github.com

はじめに
- P計画: 倒立振子の思ひ出
- 完成イメージ
目次
システム構成と前回のおさらい
- 考える系
- 導出した運動方程式と非線形状態方程式
線形化モデルの導出
線形化モデルの特性と最適レギュレータ(LQR)
- 安定性と可制御性の確認
- 最適レギュレータ(LQR)の作り方
最適レギュレータの設計例
- 台車の位置を重視した最適レギュレータ
- 振り子の角度を重視した最適レギュレータ
まとめと今後の課題
- 本記事で述べたこと
- 今後の課題
  - 可観測性とオブザーバについて
  - 運動方程式と状態方程式の導出について
付録

システム構成と前回のおさらい

ここでは前回から取り扱っている台車形倒立振子のシステム構成を振り返り，導出した運動方程式と非線形状態方程式を再掲します。

考える系

図3に，考える台車形倒立振子の全体図を示します。水平方向をx軸，垂直方向をz軸とします。今は考えませんが奥行方向がy軸ですね。なお，図3では台車を長方形で描いていますが，本記事では力学的に質点として扱います。そのため，台車のz座標は零で，振り子を取り付けたピボットのz座標も零とします（アニメーションを作る際には，台車が適当な大きさをもつものとして描きます）。

質量Mの台車の重心*3に質量m，長さ2lの振り子が取り付けられています。振り子の重心はちょうど真ん中，ピボットからlの距離にあるとします。台車のx座標をx_c，振り子の重心のx座標をx_p，同z座標をz_pとし，振り子の鉛直上向きからの角度をθとします。

振り子を倒立させ続けるため，台車には制御力fを加えます。また，外乱として振り子の先端には外乱力f_dが加わるものとします。さらに，台車には速度に比例した摩擦力μ_c dx_c / dt，振り子には角速度に比例した摩擦力μ_pdθ / dtが生じるものとします。

導出した運動方程式と非線形 状態方程式

詳細は前回をご覧頂くとして，図3の系に関する運動方程式を以下のように導出しました。

$(M + m) \ddot{x}_{c} + m l \ddot{\theta} \cos \theta = -\mu_{c} \dot{x}_{c} + m l \dot{\theta}^{2} \sin \theta + f \tag{1}$

$m l \ddot{x}_{c} \cos \theta + (J + m l^{2}) \ddot{\theta} = -\mu_{p} \dot{\theta} + m g l \sin \theta + f_{d} \cos \theta \tag{2}$

また，(1)，(2)式を $\ddot{x}_{c}$ と $\ddot{\theta}$ の連立方程式だとみなして解けば，

$\begin{align} \ddot{x}_{c} &= \left ( J f + J m l \dot{\theta}^{2} \sin \theta - J \mu_{c} \dot{x}_{c} \right . \\[10pt] &+ m l^{2} f - m l f_{d} \cos^{2} \theta - m^{2} l^{2} g \sin \theta \cos \theta \\[10pt] &\left . + m^{2} l^{3} \dot{\theta}^{2} \sin \theta - m l^{2} \mu_{c} \dot{x}_{c} + m l \mu_{p} \dot{\theta} \cos \theta \right ) / D \end{align} \tag{3}$

および

$\begin{align} \ddot{\theta} =& \left (M f_{d} \cos \theta + M m g l \sin \theta - M \mu_{p} \dot{\theta} \right . \\[10pt] &- m l f \cos \theta + m f_{d} \cos \theta + m l^{2} g \sin \theta \\[10pt] &\left . - m^{2} l^{2} \dot{\theta}^{2} \sin \theta \cos \theta + m l \mu_{c} \cos \theta \dot{x}_{c} - m \mu_{p} \dot{\theta} \right ) / D \end{align} \tag{4}$

を得ます。ただし，

$D = J (M + m) + M m l^{2} + (m l \sin \theta)^{2} \tag{5}$

です。

本記事では(3)，(4)式を線形化して状態空間モデルを導きますが，その準備として，このシステムを以下のようにも書いておきましょう。まず，状態 $\boldsymbol{x}$ と入力 $\boldsymbol{u}$ を

$\boldsymbol{x} = [x_{c}, \dot{x}_{c}, \theta, \dot{\theta} ]^{T}, \qquad \boldsymbol{u} = [f, f_{d} ]^{T} \tag{6}$

とし，非線形状態方程式を

$\displaystyle \frac{d}{dt} \begin{bmatrix} x_{c} \\ \dot{x}_{c} \\ \theta \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} F_{x}(\boldsymbol{x}, \boldsymbol{u}) \\ F_{v}(\boldsymbol{x}, \boldsymbol{u}) \\ F_{\theta}(\boldsymbol{x}, \boldsymbol{u}) \\ F_{\omega}(\boldsymbol{x}, \boldsymbol{u}) \end{bmatrix} \tag{7}$

と表すこととします*4。ただし，

$F_{x} = \dot{x}_{c} \tag{8}$

$F_{\theta} = \dot{\theta} \tag{9}$

であり，F_vとF_ωはそれぞれ(3)，(4)式に対応します。

線形化モデルの導出

線形化に関する一般論

ここでは台車形倒立振子についてはいったん忘れて，一般的な非線形状態方程式とその線形化を考えてみましょう。まず，状態 $\boldsymbol{x}$ を

$\boldsymbol{x} = [x_{1}, x_{2}, \dots, x_{n} ]^{T} \tag{10}$

また，入力 $\boldsymbol{u}$ を

$\boldsymbol{u} = [u_{1}, u_{2}, \dots, u_{m} ]^{T} \tag{11}$

とする非線形なシステムがあり，その（非線形）状態方程式を

$\dot{\boldsymbol{x}} = \boldsymbol{F}(\boldsymbol{x}, \boldsymbol{u}) = \begin{bmatrix} F_{1}(\boldsymbol{x}, \boldsymbol{u}) \\ F_{2}(\boldsymbol{x}, \boldsymbol{u}) \\ \vdots \\ F_{n}(\boldsymbol{x}, \boldsymbol{u}) \end{bmatrix} \tag{12}$

と書けるものとします。

これを平衡点の周りで線形化することを考えます。状態 $\boldsymbol{x}$ を平衡点と微小変動（摂動とも呼びます）に分け，

$\boldsymbol{x} = \boldsymbol{X} + \Delta \boldsymbol{x} = [X_{1} + \Delta x_{1}, X_{2} + \Delta x_{2}, \dots, X_{n} + \Delta x_{n} ]^{T} \tag{13}$

のように，それぞれX_iとΔx_iのように書くとします(i = 1, 2, ..., n)。同様に，入力についても，

$\boldsymbol{u} = \boldsymbol{U} + \Delta \boldsymbol{u} = [U_{1} + \Delta u_{1}, U_{2} + \Delta u_{2}, \dots, U_{m} + \Delta u_{m} ]^{T} \tag{14}$

と表すものとします。これらについて微小変動のみを取り出せば，

$\Delta \boldsymbol{x} = [\Delta x_{1}, \Delta x_{2}, \dots, \Delta x_{n} ]^{T} \tag{15}$

また，

$\Delta \boldsymbol{u} = [\Delta u_{1}, \Delta u_{2}, \dots, \Delta u_{m} ]^{T} \tag{16}$

ですね。

ここで，微小変動 $\Delta \boldsymbol{x}$ ， $\Delta \boldsymbol{u}$ に着目して(12)式を線形近似すると次式のように書けます。

$\Delta \dot{\boldsymbol{x}} = \boldsymbol{A} \Delta \boldsymbol{x} + \boldsymbol{B} \Delta \boldsymbol{u} \tag{17}$

ただし，

$\boldsymbol{A} = \begin{bmatrix} \displaystyle \frac{\partial F_{1}}{\partial x_{1}} & \displaystyle \frac{\partial F_{1}}{\partial x_{2}} & \dots & \displaystyle \frac{\partial F_{1}}{\partial x_{n}} \\[5pt] \displaystyle \frac{\partial F_{2}}{\partial x_{1}} & \displaystyle \frac{\partial F_{2}}{\partial x_{2}} & \dots & \displaystyle \frac{\partial F_{2}}{\partial x_{n}} \\[5pt] \vdots & \vdots & \ddots & \vdots \\[5pt] \displaystyle \frac{\partial F_{n}}{\partial x_{1}} & \displaystyle \frac{\partial F_{n}}{\partial x_{2}} & \dots & \displaystyle \frac{\partial F_{n}}{\partial x_{n}} \end{bmatrix}_{(\boldsymbol{x}, \boldsymbol{u}) = (\boldsymbol{X}, \boldsymbol{U})} \tag{18}$

また，

$\boldsymbol{B} = \begin{bmatrix} \displaystyle \frac{\partial F_{1}}{\partial u_{1}} & \displaystyle \frac{\partial F_{1}}{\partial u_{2}} & \dots & \displaystyle \frac{\partial F_{1}}{\partial u_{m}} \\[5pt] \displaystyle \frac{\partial F_{2}}{\partial u_{1}} & \displaystyle \frac{\partial F_{2}}{\partial u_{2}} & \dots & \displaystyle \frac{\partial F_{2}}{\partial u_{m}} \\[5pt] \vdots & \vdots & \ddots & \vdots \\[5pt] \displaystyle \frac{\partial F_{n}}{\partial u_{1}} & \displaystyle \frac{\partial F_{n}}{\partial u_{2}} & \dots & \displaystyle \frac{\partial F_{n}}{\partial x_{m}} \end{bmatrix}_{(\boldsymbol{x}, \boldsymbol{u}) = (\boldsymbol{X}, \boldsymbol{U})} \tag{19}$

です。言い換えれば，線形化された状態空間モデルの $\boldsymbol{A}$ 行列， $\boldsymbol{B}$ 行列は，元の非線形状態方程式を表すベクトル値関数 $\boldsymbol{F}(\boldsymbol{x}, \boldsymbol{u})$ の平衡点でのヤコビアンであるとも言えますね*5。また別の言い方をすれば， $\boldsymbol{A}$ ， $\boldsymbol{B}$ の各成分は，非線形状態方程式 $F_{1}, F_{2}, \dots, F_{n}$ を各状態変数 $x_{1}, x_{2}, \dots, x_{n}$ や各入力 $u_{1}, u_{2}, \dots, u_{m}$ でテイラー展開（平衡点 $\boldsymbol{X}$ と $\boldsymbol{U}$ が零であればマクローリン展開）した際の1次近似と言えるかもしれません。

台車形倒立振子への適用

以上を踏まえて台車形倒立振子を表現する非線形状態方程式を平衡点の周りで線形近似しましょう。平衡点 $\boldsymbol{X}$ ， $\boldsymbol{U}$ はもちろん外力なしで倒立して原点で静止している状態，すなわち，

$\boldsymbol{X} = [0, 0, 0, 0]^{T}, \qquad \boldsymbol{U} = [0, 0]^{T} \tag{20}$

です。この条件でヤコビアンを計算し，線形化された状態空間モデルの $\boldsymbol{A}$ 行列， $\boldsymbol{B}$ 行列を求めますが， $\boldsymbol{A}$ の第1行，第3行は(7) ~ (9)式からそれぞれ[0, 1, 0, 0]および[0, 0, 0, 1]となることが直ちに分かります。すなわち，

$\boldsymbol{A} = \begin{bmatrix} 0 & 1 & 0 & 0 \\[5pt] \displaystyle \frac{\partial F_{v}}{\partial x_{c}} & \displaystyle \frac{\partial F_{v}}{\partial \dot{x}_{c}} & \displaystyle \frac{\partial F_{v}}{\partial \theta} & \displaystyle \frac{\partial F_{v}}{\partial \dot{\theta}} \\[5pt] 0 & 0 & 0 & 1 \\[5pt] \displaystyle \frac{\partial F_{\omega}}{\partial x_{c}} & \displaystyle \frac{\partial F_{\omega}}{\partial \dot{x}_{c}} & \displaystyle \frac{\partial F_{\omega}}{\partial \theta} & \displaystyle \frac{\partial F_{\omega}}{\partial \dot{\theta}} \end{bmatrix}_{(\boldsymbol{x}, \boldsymbol{u}) = (\boldsymbol{X}, \boldsymbol{U})} \tag{21}$

と書けます。本丸は第2行，第4行ですね。同様に， $\boldsymbol{B}$ については，

$\boldsymbol{B} = \begin{bmatrix} 0 & 0 \\[5pt] \displaystyle \frac{\partial F_{v}}{\partial f} & \displaystyle \frac{\partial F_{v}}{\partial f_{d}} \\[5pt] 0 & 0 \\[5pt] \displaystyle \frac{\partial F_{\omega}}{\partial f} & \displaystyle \frac{\partial F_{\omega}}{\partial f_{d}} \end{bmatrix}_{(\boldsymbol{x}, \boldsymbol{u}) = (\boldsymbol{X}, \boldsymbol{U})} \tag{22}$

です。

SymPyで偏微分係数を求める

(21)，(22)式に含まれる12個の偏微分を求めますが，やはり数学弱者*6としてはSymPyの力添えに頼ることになります。例として，(21)式の $\boldsymbol{A}$ 行列の(2, 2)成分である

$A_{22} = \left . \displaystyle \frac{\partial F_{v}}{\partial \dot{x}_{c}} \right |_{(\boldsymbol{x}, \boldsymbol{u}) = (\boldsymbol{X}, \boldsymbol{U})} \tag{23}$

を求めてみましょう（A₂₁は零になって面白くないのでA₂₂を例とします）。途中までは前回と同じ処理です。

まずはSymPyをインポートします。また，前回同様にドットで時間微分を表すニュートン式の表記をするためにdynamicsymbolsとinit_vprintingもインポートします。

import sympy as sp
from sympy.physics.mechanics import dynamicsymbols, init_vprinting
init_vprinting()

各シンボルを定義します。

# Symbols for cart
x_c = dynamicsymbols('x_c')
M, mu_c = sp.symbols('M mu_c')

# Symbols for pendulum
theta = dynamicsymbols('theta')
m, l, J, mu_p = sp.symbols('m l J mu_p')

# Symbol for external force
f = sp.symbols('f')

# Symbol for disturbance at tip of pendulum
f_d = sp.symbols('f_d') 

# Symbol for gravity acceleration
g = sp.symbols('g')

# Time
t = sp.symbols('t')

導出した運動方程式である(1)，(2)式をSymPyの方程式（Eqクラス）として定義します。

# Define equations
eq1 = sp.Eq((M + m) * x_c.diff(t, 2) \
    + m * l * theta.diff(t, 2) * sp.cos(theta), \
    -mu_c * x_c.diff(t) + \
    m * l * theta.diff(t)**2 * sp.sin(theta) + f)
eq2 = sp.Eq(m * l * x_c.diff(t, 2) * sp.cos(theta) \
    + (J + m * l**2) * theta.diff(t, 2), \
    -mu_p * theta.diff(t) \
    + m * g * l * sp.sin(theta) + f_d * sp.cos(theta))

上記プログラムのeq1とeq2はそれぞれ(1)，(2)式に相当します。これを $\ddot{x}_{c}$ と $\ddot{\theta}$ の単純な連立1次方程式として解いて，(3)，(4)式の形式を得ます。

# Solve system of equations
sol = sp.solve([eq1, eq2], [x_c.diff(t, 2), theta.diff(t, 2)])

解を変数solに格納しました。 $\ddot{x}_{c}$ に関する解（(3)式に相当）を抽出し，simplifyしながら変数F_vに格納します。

F_v = sol[x_c.diff(t, 2)].simplify()

これに対して(23)式の偏微分係数を計算します。diffメソッドでx_c.diff(t, 1)（すなわち $\dot{x}_{c}$ ）について（偏）微分した後，subsメソッドで各状態変数に平衡点である零を代入しています。

# Derive twelve partial differential coefficients
# around x = [0, 0, 0, 0]^T and u = [0, 0]^T
# A matrix of the system
A22 = F_v.diff(x_c.diff(t, 1), 1).subs([ \
    (x_c, 0), \
    (x_c.diff(t, 1), 0), \
    (theta, 0), \
    (theta.diff(t, 1), 0)]).simplify()
display(A22)

このように，台車の速度 $\dot{x}_{c}$ ，すなわちPython上ではx_cをtで微分したものであるx_c.diff(t, 1)でF_vを微分するわけです。JupyterLabで使えるdisplay関数で結果を表示すると，

$A_{22} = \displaystyle \frac{\mu_{c} \left(- J - l^{2} m\right)}{J M + J m + M l^{2} m} \tag{25a}$

を得ます。ちょいと整理して，

$A_{22} = - \displaystyle \frac{\mu_{c} \left(J + m l^{2} \right)}{J (M + m) + M m l^{2}} \tag{25b}$

と書き換えてみます。この分母の部分は他の偏微分係数についても共通なので，

$K = \displaystyle \frac{1}{J (M + m) + M m l^{2}} \tag{26}$

とおくことにします。

線形化した台車形倒立振子のA，B行列

以上を繰り返せば， $\boldsymbol{A}$ 行列として次式を得ます。

$\boldsymbol{A} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & -K \mu_{c} (J + m l^{2}) & -K m^{2} l^{2} g & K \mu_{p} m l \\ 0 & 0 & 0 & 1 \\ 0 & K \mu_{c} m l & K m l g (M + m) & -K \mu_{p} (M + m) \end{bmatrix} \tag{27}$

同様に $\boldsymbol{B}$ 行列は

$\boldsymbol{B} = \begin{bmatrix} 0 & 0 \\ K (J + m l^{2}) & -K m l \\ 0 & 0 \\ -K m l & K (M + m) \end{bmatrix} \tag{28}$

と計算できます。SymPyの力です💪*7

線形化モデルの特性と最適レギュレータ(LQR)

以上のように，台車形倒立振子の線形化モデルを導出できました。(12)式を再掲すると

$\Delta \dot{\boldsymbol{x}} = \boldsymbol{A} \Delta \boldsymbol{x} + \boldsymbol{B} \Delta \boldsymbol{u} \tag{29}$

となりますが，以下では微小変動を表す“ $\Delta$ ”は省略して，普通の線形状態空間モデルのように，

$\dot{\boldsymbol{x}} = \boldsymbol{A} \boldsymbol{x} + \boldsymbol{B} \boldsymbol{u} \tag{30}$

と書いてしまうことにします。 $\boldsymbol{A}$ ， $\boldsymbol{B}$ 行列はそれぞれ(27)，(28)式で求めてあります。

安定性と可制御性の確認

現代制御理論の初歩の復習も兼ねて，安定性と可制御性を確認してみましょう（とは言っても，不安定かつ可制御であることは明らかですが…）。前回と同様に，台車の質量M = 1 kg，振り子の質量m = 0.75 kg，振り子の長さ2l = 60 cm，台車と床面の摩擦に関する減衰係数μ_c = 0.05 N/(m/s)，振り子の摩擦に関する減衰係数μ_p = 0.05 N/(rad/s)とします。振り子を一様な細い棒と考えると，振り子の重心の周りの慣性モーメントJ = ml² / 3となります。

from scipy.constants import g

# Parameters
M = 1.00                  # Mass of cart
m = 0.75                  # Mass of pendulum, kg
l = 0.30                  # Half length, m
J = m * l**2 / 3          # Inertia around center of mass, kg m**2
mu_c = 0.050              # Friction of cart, N/(m/s)
mu_p = 0.050              # Friction of pendulum, Nm/(rad/s)

これらのパラメータを使って $\boldsymbol{A}$ 行列， $\boldsymbol{B}$ 行列をそれぞれ定義します。

# Matrices as a result of linearization
K = 1 / (J * (M + m) + M * m * l**2)
A = np.array([[0, 1, 0, 0],
              [0, -K * mu_c * (J + m * l**2), -K * m**2 * l**2 * g, mu_p * m * l],
              [0, 0, 0, 1],
              [0, K * mu_c * m * l, K * m * l * g * (M + m), -K * mu_p * (M + m)]])
B = np.array([[0, 0],
              [K * (J + m * l**2), -K * m * l],
              [0, 0],
              [-K * m * l, K * (M + m)]])

この条件で， $\boldsymbol{A}$ 行列とその固有値を確認します。

# Confirm eigenvalues of A
print(f'A =\n{A}')
w, v = np.linalg.eig(A)
print(f'Eigenvalues =\n{w}')

すると，

A =
[[ 0.00000000e+00  1.00000000e+00  0.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00 -4.21052632e-02 -4.64525526e+00  1.12500000e-02]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]
 [ 0.00000000e+00  1.05263158e-01  3.61297632e+01 -8.18713450e-01]]
Eigenvalues =
[ 0.         -0.02857895 -6.44052156  5.60828179]

と出力されます。 $\boldsymbol{A}$ の固有値については4つ目が正(5.60828179 > 0)となっているため，不安定であることが判ります。

可制御性も確認してみましょう。可制御行列

$\boldsymbol{U}_{c} = \left [ B, A B, A^{2} B, A^{3} B \right ] \tag{31}$

を計算してみます。ただし，(28)式で求めた $\boldsymbol{B}$ では，その1列目が制御力のための成分となっているため，可制御性の確認にあたってはこれのみをスライスします。

# Check controllability
B_c = B[:, 0]  # Extract part of B for control force to the cart
print(f'B =\n{B_c}')
U_c = np.array([B_c,
                A @ B_c,
                A @ A @ B_c,
                A @ A @ A @ B_c])
print(f'U_c =\n{U_c}')
print(f'Rank of U_c = {np.linalg.matrix_rank(U_c)}')

なお，Aをnumpy.matrixではなくnumpy.ndarrayとして定義したため，例えばA**2とするとAの要素毎の2乗が計算されてしまいます。力技ですが，@演算子でAを必要回数掛けることにしました*8。結果として，

B =
[ 0.          0.84210526  0.         -2.10526316]
U_c =
[[ 0.00000000e+00  8.42105263e-01  0.00000000e+00 -2.10526316e+00]
 [ 8.42105263e-01 -5.91412742e-02 -2.10526316e+00  1.81224992e+00]
 [-5.91412742e-02  9.80236274e+00  1.81224992e+00 -7.75525981e+01]
 [ 9.80236274e+00 -9.70356128e+00 -7.75525981e+01  1.30001343e+02]]
Rank of U_c = 4

と出力されます。ランクが4，すなわちフルランクであることから可制御であることを確認できました。

今回はNumPyだけでこのような確認をしましたが，Python Control System Library (python-control)を使えばもっとシンプルに計算できるはずです*9。

最適レギュレータ(LQR)の作り方

次式で表される評価関数Jを最小化するコントローラを最適レギュレータ(LQR, linear quadratic regulator)といいます。

$J = \displaystyle \int_{0}^{\infty} \left (\boldsymbol{x}^{T} (t) \boldsymbol{Q} \boldsymbol{x} (t) + \boldsymbol{u}^{T} (t) \boldsymbol{R} \boldsymbol{u} (t) \right ) dt \tag{32}$

ただし， $\boldsymbol{Q} (= \boldsymbol{Q}^{T} > 0)$ は状態 $\boldsymbol{x}$ に関する重み行列， $\boldsymbol{R} (= \boldsymbol{R}^{T} > 0)$ は入力 $\boldsymbol{u}$ に関する重み行列です。最適レギュレータの状態フィードバックゲイン $\boldsymbol{F}_{\mathrm{opt}}$ は，

$\boldsymbol{F}_{\mathrm{opt}} = -\boldsymbol{R}^{-1} \boldsymbol{B}^{T} \boldsymbol{P} \tag{33}$

として得ることができます。ただし， $\boldsymbol{P} (= \boldsymbol{P}^{T} > 0)$ はRiccati方程式

$\boldsymbol{A}^{T} \boldsymbol{P} + \boldsymbol{P} \boldsymbol{A} + \boldsymbol{P} \boldsymbol{B} \boldsymbol{R}^{-1} \boldsymbol{B}^{T} \boldsymbol{P} + \boldsymbol{Q} = 0 \tag{34}$

の解です（どうしてこうなるのか，筆者はまったく理解していません…💧）。(32)式を見ると，状態 $\boldsymbol{x}(t)$ が素早く零に収束すること，また，入力 $\boldsymbol{u}(t)$ が小さくなることによって，評価関数Jが小さくなります。状態 $\boldsymbol{x}(t)$ の収束（ $\boldsymbol{x}$ の要素であるそれぞれの状態変数毎の収束）と入力 $\boldsymbol{u}(t)$ が大きくならないこと（台車形倒立振子では台車に加える制御力が大きくなりすぎないこと）のいずれを重視するかで $\boldsymbol{Q}$ と $\boldsymbol{R}$ に設定する値を変えると，自動的にその目的に合致する状態フィードバックゲインが求まります。

「最適」と言っても「何について最適であるか」は重み $\boldsymbol{Q}$ ， $\boldsymbol{R}$ で決まりますので，結局， $\boldsymbol{Q}$ と $\boldsymbol{R}$ を変えてみるという試行錯誤は必要かと思われます。ただし，これでも状態フィードバックゲインを直接変えて試行錯誤するよりはるかに効率的です。というのも，（線形化モデルに対してであれば）必ず制御できる状態フィードバックゲインが選ばれるからです（状態フィードバックゲインを直接あれこれしていると，制御できない組み合わせとなることがあり得ます）。なお，台車形倒立振子のように（制御としては）1入力である場合， $\boldsymbol{R}$ はスカラーになります。

最適レギュレータの設計例

「設計」と呼ぶのは烏滸がましいですが，例として2つほどLQRをやってみたいと思います。

台車の位置を重視した最適レギュレータ

例として，台車の位置が原点に戻るスピードを重視した最適レギュレータを設計してみます。まず，以下のようにNumPyとSciPyのlinalgからsolve_continuous_are関数をインポートします。

import numpy as np
from scipy.linalg import solve_continuous_are

以下のように，solve_continuous_are関数を使ってRiccati方程式を解くことができます。bについては制御力の部分のみを考慮するのでBの1列目のみをスライスしています（可制御性の確認の際に作ったB_cとほぼ同じですが，ここでのbは縦ベクトルとして定義しています）。重み行列Qとしては，diagを使って対角成分のみをもつ行列を定義しています。Q₁₁ = 500，Q₃₃ = 1として，1つ目の状態変数，すなわち台車の位置x_cを重視する重みを設定しました。また，R = [1]を設定して，入力の重みを小さくしました。

# LQR, using linearized state-space model
# Weights
b = np.array([B[:, 0]]).T
Q = np.diag([500, 0, 1, 0])
R = np.array([[1]])

# Solve Riccati equation
P = solve_continuous_are(A, b, Q, R)
F = (-np.linalg.inv(R) @ b.T @ P)[0]
print(f'State-feedback gain F =\n{F}')

# Check eigenvalues of closed-loop system
w_lqr, v_lqr = np.linalg.eig(A + b * F)
print(f'Eigenvalues of closed-loop system =\n{w_lqr}')

この条件で8行目のようにRiccati方程式の解Pを求めます。さらに次の行でPから状態フィードバックゲインFを得ています。最後にprint関数でFと，閉ループ系の固有値を表示しますが，その出力は以下となります。

State-feedback gain F =
[22.36067977 17.70639743 85.52231946 14.89540441]
Eigenvalues of closed-loop system =
[-5.85621477+0.21294118j -5.85621477-0.21294118j -2.79824242+2.36919575j
 -2.79824242-2.36919575j]

閉ループ系の固有値の実部はすべて負になっており，安定化できていることが判ります。以上で状態フィードバックゲインFが得られました。

このようにして得られた状態フィードバックゲインFは，あくまでも線形化モデルに対して設計したゲインです。非線形な元のシステムに対して有効かどうかは，シミュレーションしてみなければ分かりません*10。非線形な元のシステムの求解については前回を参照頂くとして，SciPyのsolve_ivp関数を用いる場合の線形化モデル（状態空間モデル）を記述する関数を書いておきます。

# Differential equation, linearized
# State x = [x_c, x_c_dot, theta, theta_dot]^T
def func_lin(t, x):
    # Extract variables
    x_c, x_c_dot, theta, theta_dot = x
    
    # External force applied to cart as control input    
    f = force_control(t, x)
    
    # External force applied at tip of pendulum as disturbance
    f_d = force_disturbance(t, x)
    
    u = np.array([f, f_d])
    
    # Prepare empty array to store derivatives
    dxdt = np.zeros_like(x)
    
    # Differential equation
    dxdt = A @ x + B @ u
    
    return dxdt

直観的でシンプルです*11。

台車の初期位置x_c0 = −1 m，振り子の初期角度θ₀ = −30°として，時刻t = 5 sでステップ的な外乱，時刻t = 9 sから3秒間にわたって正弦波外乱を加えた場合を計算しました（線形化モデルでは前回のような「振り上げ」は再現できません）。図4に得られた最適レギュレータを用いた場合の非線形な元のシステムと線形化モデルの時間波形を示します。

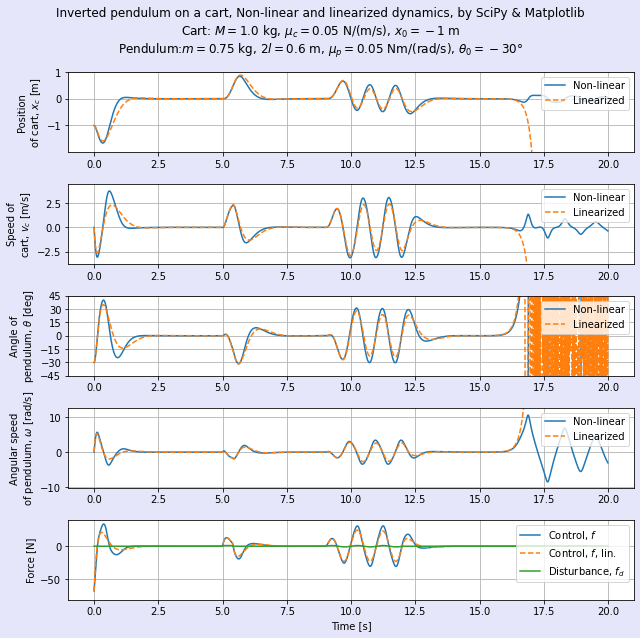
台車の位置x_cは速やかに原点(x_c = 0 m)に戻っているように見えます*12。これでは分かり難いのでやはりアニメーションも表示しましょう。

図5: 台車の位置x_cを重視した最適レギュレータを適用した場合のアニメーション

図5に台車の位置を重視した最適レギュレータを適用した場合のアニメーションを示します。非線形な元のシステムに対して，薄いゴーストのような線形化モデルの台車が追従しています。また，線形化モデルを用いて設計した状態フィードバックゲインを用いて，非線形な元のシステムを制御できていることが判ります。

振り子の角度を重視した最適レギュレータ

次に，振り子の角度θがなるべく0°をキープするような最適レギュレータを考えてみます。

# LQR, using linearized state-space model
# Weights
b = np.array([B[:, 0]]).T
Q = np.diag([1, 0, 500, 0])
R = np.array([[1]])

# Solve Riccati equation
P = solve_continuous_are(A, b, Q, R)
F = (-np.linalg.inv(R) @ b.T @ P)[0]
print(f'State-feedback gain F =\n{F}')

# Check eigenvalues of closed-loop system
w_lqr, v_lqr = np.linalg.eig(A + b * F)
print(f'Eigenvalues of closed-loop system =\n{w_lqr}')

先ほどの例とはQの500と1を入れ替えました*13。結果として，

State-feedback gain F =
[ 1.          2.72644047 52.27353179  7.65506225]
Eigenvalues of closed-loop system =
[-6.92096699+3.38181947j -6.92096699-3.38181947j -0.4194277 +0.41475428j
 -0.4194277 -0.41475428j]

を得ます。閉ループ系の固有値の実部はやはり負となっているので，やはり安定化はできています。定性的には台車を急激に動かすことを避けることによって，振り子があまり傾かないようにするのではないかと思われますね。図6に時間波形を示します。

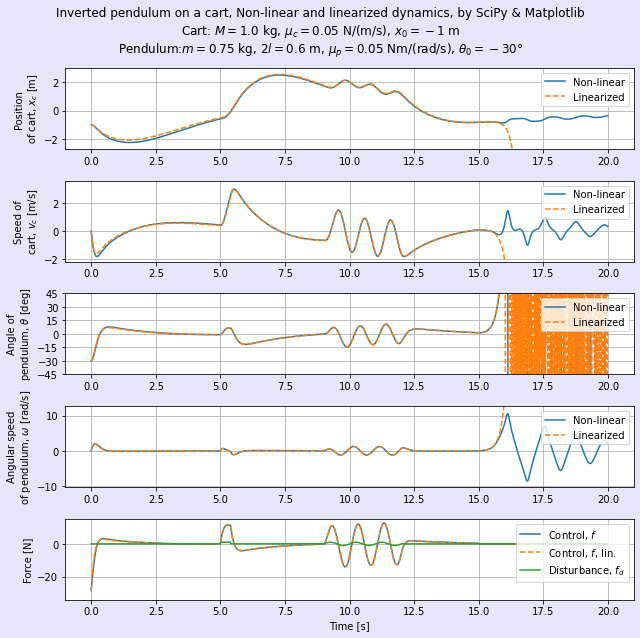
台車の位置x_cは原点を離れている時間帯が長くなっています。図7にアニメーションも表示してみましょう（実は冒頭の図2の再掲です）。

外乱があってもそれをいなす*14ような動きになっていて，その代わり台車を原点から離すことを許容していますね。図5とは性格を異にする制御と言えそうです。

まとめと今後の課題

本記事で述べたこと

本記事では台車形倒立振子の非線形な運動方程式・状態方程式を線形化して線形状態空間モデルを導出しました。導出の際には非線形状態方程式のヤコビアンを計算するのですが，筆者のような数学弱者の心強い味方であるSymPyを活用しました。

また，導出した線形状態空間モデルに基づいて最適レギュレータ(LQR, linear quadratic regulator)を設計し，元の非線形な台車形倒立振子を制御できることをアニメーションで可視化しました。

今後の課題

可観測性とオブザーバについて

お気付きとは思いますが，今回はすべての状態変数を観測できるという前提で議論を進めました。しかし，台車の位置x_cと速度v_c，振り子の角度θと角速度ωのすべてをセンサで捉えることは実質的に難しい場合が多いのではないかと考えます。特に，（本ブログでも使用したことがありますが）MPU6050のような加速度・ジャイロセンサを振り子に取り付けた場合，振り子の角速度ωは判っても，振り子の角度θはωを時間積分するとして，台車の位置や速度を推定できるのかといった問題があります。

可観測性を確認してみましたが，台車の位置x_cを直接観測しないと系全体としては可観測にならないようです。例えば，台車の位置以外の3つの状態変数を観測した場合，残念ながら不可観測になります。

# Check observability
C = np.array([0, 1, 1, 1])
U_o = np.array([C,
                C @ A,
                C @ A @ A,
                C @ A @ A @ A])
print(f'C = \n{C}')
print(f'U_o =\n{U_o}')
print(f'Rank of U_o = {np.linalg.matrix_rank(U_o)}')

この出力は以下となります。

C = 
[0 1 1 1]
U_o =
[[ 0.00000000e+00  1.00000000e+00  1.00000000e+00  1.00000000e+00]
 [ 0.00000000e+00  6.31578947e-02  3.14845079e+01  1.92536550e-01]
 [ 0.00000000e+00  1.76077255e-02  6.66291540e+00  3.13275862e+01]
 [ 0.00000000e+00  3.29689927e+00  1.13177648e+03 -1.89852027e+01]]
Rank of U_o = 3

状態変数の数が4つであるところ， $\boldsymbol{U}_{o}$ のランクが3となってしまうため，不可観測です。逆に，台車の位置を観測しさえすれば，可観測になるようです。上記のプログラムの2行目をC = np.array([1, 0, 0, 0])と書き換えて確認してみると，

C = 
[1 0 0 0]
U_o =
[[ 1.00000000e+00  0.00000000e+00  0.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00  1.00000000e+00  0.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00 -4.21052632e-02 -4.64525526e+00  1.12500000e-02]
 [ 0.00000000e+00  2.95706371e-03  6.02049531e-01 -4.65493947e+00]]
Rank of U_o = 4

となり，フルランクであることから可観測となり，オブザーバを構築できるはずです。

いずれにしても，どのように状態変数を観測・推測するかについては，今後の検討課題となりますね。ただし，ひとまず台車形倒立振子はお休みにして，作りたいを思っている車輪形倒立振子のモデル化に進みたいと思います（そこでもこのセンシングの問題は残ります）。

運動方程式と状態方程式の導出について

不勉強ながら，本記事で述べた事柄に取り組んでいる最中に知りましたが，SymPyには力学を取り扱う仕組みが備わっているようです。

docs.sympy.org

質点や剛体を定義し，運動エネルギーと位置エネルギーからラグランジアンを記述できれば，運動方程式を自動的に導くことができるようです。これならば，筆者のような数学弱者が貧弱な腕力で導出するよりも確実ですし，系の形が変わった場合にも対応が容易になります。また，SymPyで導出した数式をNumPyで扱える関数に変換するLambdifyという仕組みがありますので（本ブログでも過去に使ったことがあります），SymPyで導出した運動方程式・状態方程式をそのままSciPyでのシミュレーションに使えるようにすることもできるはずです。ヤコビアンを使った線形化もできるのではないかと思います。

また，やはり制御系ということでPython Control System Library (python-control)を活用した方が良いのではないかとも考えています。こちらは恐らく，数値的だと思いますが，非線形なシステムの線形化もできるようです。

次に取り組む予定の車輪形倒立振子ではSymPyとpython-controlの機能を活かしたモデル化を推し進めたいと考えています。

付録

台車形倒立振子の線形化に関して，ヤコビアンを使わないでsinとcosの微小角度での近似から求めることもできます。運動方程式を再掲します。

$(M + m) \ddot{x}_{c} + m l \ddot{\theta} \cos \theta = -\mu_{c} \dot{x}_{c} + m l \dot{\theta}^{2} \sin \theta + f \tag{35}$

$m l \ddot{x}_{c} \cos \theta + (J + m l^{2}) \ddot{\theta} = -\mu_{p} \dot{\theta} + m g l \sin \theta + f_{d} \cos \theta \tag{36}$

ここで， $\theta$ や $\dot{\theta}$ が小さい場合，電気工学などでも常套手段ですが，

$\begin{align} \sin \theta & \simeq \theta \\[5pt] \cos \theta & \simeq 1 \\[5pt] \dot{\theta}^{2} \sin & \theta \simeq 0 \end{align} \tag{37}$

と近似することにします。すると，

$(M + m) \ddot{x}_{c} + m l \ddot{\theta} = -\mu_{c} \dot{x}_{c} + f \tag{37}$

$m l \ddot{x}_{c} + (J + m l^{2}) \ddot{\theta} = -\mu_{p} \dot{\theta} + m g l \theta + f_{d} \tag{38}$

と書くことができます。これを $\ddot{x}_{c}$ と $\ddot{\theta}$ について解いて整理すれば，(27)，(28)式と同じ $\boldsymbol{A}$ 行列と $\boldsymbol{B}$ 行列を得られます。

*1:AMD Duron (600 MHz)で動いていた3代前のメインPCで書いたもの

*2:筆者が不勉強なだけという可能性が最も高いです。

*3:本記事では台車を質点として扱っています。台車が回転しないという条件下では，必ずしも重心でなくても良さそうです。「台車」と呼びながら車輪はありませんね…。

*4:外乱力f_dもひとまず入力とみなします。

*5:だ…だよね…？（数学弱者の一抹の不安😅）

*6:本ブログの筆者の数学力は著しく弱いことが一般に広く知られています。

*7:ただし，本記事ではSymPyの真の力をまだ引き出すことができていません。次回以降，SymPyの力学系を取り扱う機能を活かして車輪形倒立振子のモデル化に挑みます。

*8:numpy.linalg.matrix_power関数を使えば，numpy.ndarrayとして定義された配列についても行列としての累乗を計算できます。

*9:例えば南裕樹先生の「Pythonによる制御工学入門」（オーム社，2019年）などをご参照下さい。

*10:シミュレーションしてみても限られた条件下での挙動しか分からないかもしれません。

*11:Python Control System Library (python-control)を使えばもっと簡単だったのかもしれません

*12:よね？

*13:本来，台車の位置x_cと振り子の角度θは単位も動く範囲も異なるので，Qをこのように乱暴に設定して良いのかどうか，筆者には分かりませんでした。Qのそれぞれの要素は異なる単位を持つはずですが，制御工学の教科書などで言及されている例を浅学ながら見たことがありません。

*14:良い表現を思いついたかも…？

The Negligible Lab

Astray in the forest of electrical and electronic circuits. Adrift in the gap between time and frequency domains. 独立独歩を是とする。