三相LCL回路のd-q座標系におけるインピーダンスを求める

はじめに

系統連系インバータと電力系統の相互作用によって，システムが不安定になることがあります。本ブログでは，過去の記事にて電流制御系と系統インピーダンスの相互作用について検討したことがあります。系統連系インバータの外乱応答（インピーダンス）と系統インピーダンスの比のナイキスト線図を描くことによって，電流制御系の安定性を論じることができました。しかし，この記事では単相の場合しか取り扱っておりませんでした。三相の場合はどのように考えるべきでしょうか。

negligible.hatenablog.com

三相系統連系インバータは大体においてd-q（回転）座標系で制御することが一般的であり，かつ，d軸とq軸で別々の制御を行っています。したがって，三相系統連系インバータはd-q座標系で不平衡なインピーダンスとなることでしょう。そのため，一般的に三相平衡に近いと考えられる系統インピーダンスの方を三相（あるいはα-β（静止）座標系）からd-q座標系に換算して表現するのが好適と考えられます。

しかし，不幸にして筆者は，RL直列回路以外の一般のインピーダンスをd-q座標系で表現する方法を，よくよく考えてみると知りませんでした。その必要性があること自体を想像できておらず，自らの不明を恥じ入っております。

そこで，本記事では，任意のインピーダンスをd-q座標系で表現する手法について，文献を紹介しながら説明します。また，一例として三相LCL回路のインピーダンスのd-q座標系における表現を導出し，これをLTspiceでの周波数スキャン(frequency response analysis, FRA)と比較検証することとしました。

任意のインピーダンスの場合と文献紹介

任意のインピーダンスのd-q座標系での表現

まず，ずばり結論を述べます。あくまでも三相平衡の場合を前提としますが，s領域において，三相座標系での自己インピーダンスがZ_s(s)，相互インピーダンスがZ_m(s)である場合，次式が成り立ちます。

$\begin{bmatrix} V_{a}(s) \\ V_{b}(s) \\ V_{c}(s) \end{bmatrix} = \begin{bmatrix} Z_{s}(s) & Z_{m}(s) & Z_{m}(s) \\ Z_{m}(s) & Z_{s}(s) & Z_{m}(s) \\ Z_{m}(s) & Z_{m}(s) & Z_{s}(s) \end{bmatrix} \begin{bmatrix} I_{a}(s) \\ I_{b}(s) \\ I_{c}(s) \end{bmatrix} \tag{1}$

上式をα-β座標系で表現すると，

$\begin{bmatrix} V_{\alpha}(s) \\ V_{\beta}(s) \end{bmatrix} = \begin{bmatrix} Z^{s}(s) & 0 \\ 0 & Z^{s}(s) \end{bmatrix} \begin{bmatrix} I_{\alpha}(s) \\ I_{\beta}(s) \end{bmatrix} \tag{2}$

となって，α軸とβ軸の干渉はなくなります。ただし，

$Z^{s}(s) = Z_{s}(s) - Z_{m}(s) \tag{3}$

であり，上付きsはstationary = 静止座標系を意味します。これを角速度ω₁で回転するd-q座標系で表現した場合，次式となります。

$\begin{bmatrix} V_{d}(s) \\ V_{q}(s) \end{bmatrix} = \begin{bmatrix} Z_{d}(s) & -Z_{q}(s) \\ Z_{q}(s) & Z_{d}(s) \end{bmatrix} \begin{bmatrix} I_{d}(s) \\ I_{q}(s) \end{bmatrix} \tag{4}$

ここで，若干数学的に厳密な書き方ではありませんが，

$\begin{align} Z_{d}(s) &= \mathrm{Re} \left [ Z^{s}(s + j \omega_{1}) \right ] \\ Z_{q}(s) &= \mathrm{Im} \left [ Z^{s}(s + j \omega_{1}) \right ] \end{align} \tag{5}$

と表現できます。ここで，上式で実部と虚部を取り出すReとImを計算する場合，ひとまずラプラス演算子sを実数と見なして計算します。

文献紹介

d-q座標系での任意のインピーダンスの表現方法については，以下の論文にて詳しく述べられております。以下，この論文を「Harnefors氏の論文」と呼ぶことにします。

ieeexplore.ieee.org

Harnefors氏の論文では，上記の(5)式よりも数学的に厳密な書き方をしている他，三相不平衡な場合についての取り扱いについても記載しております。ただし，三相不平衡な場合については~~筆者の理解が追い付いていないため~~煩雑になるため，まず本記事では三相平衡な場合に限定します。

以降，RL直列回路とLCL回路の場合を例に挙げながら，実際に計算していきます。

はじめに
任意のインピーダンスの場合と文献紹介
- 任意のインピーダンスのd-q座標系での表現
- 文献紹介
目次
三相RL直列回路の場合
三相LCL回路の場合
計算例
まとめ
今後の議論
- Zs(jω)の数値データからZd(jω)，Zq(jω)を得られるか
- 不平衡な場合
付録1: 係数A, B, C, D
付録2: 三相RL直列回路においてα-β座標系での表現を出発点とした場合

三相RL直列回路の場合

筆者が知っていた求め方

本ブログの過去の記事*1でも述べましたが，三相RL直列回路のインピーダンスをd-q座標系で表現する道筋をおさらいしたいと思います。図1に三相RL直列回路とそのd軸，q軸等価回路，およびブロック線図を示します。

f:id:s-inoue2010:20210428090021p:plain:w300 — 図1: 三相RL直列回路とそのd軸，q軸等価回路，ブロック線図

当たり前のことですが，図1(a)では次式が成立します。

$\begin{bmatrix} v_{a} \\ v_{b} \\ v_{c} \end{bmatrix} = R \begin{bmatrix} i_{a} \\ i_{b} \\ i_{c} \end{bmatrix} + L \displaystyle \frac{d}{dt} \begin{bmatrix} i_{a} \\ i_{b} \\ i_{c} \end{bmatrix} \tag{6}$

ここで，電圧・電流ベクトルに対して（零相成分を含めて）逆d-q変換と逆α-β変換を施すための行列を[C]をすると*2，[C]は

$\displaystyle [ C ] = \sqrt{\frac{2}{3}} \begin{bmatrix} \frac{1}{\sqrt{2}} & \cos \theta_{1} & -\sin \theta_{1} \\ \frac{1}{\sqrt{2}} & \cos \left (\theta_{1} - \frac{2 \pi}{3} \right ) & -\sin \left (\theta_{1} - \frac{2 \pi}{3} \right ) \\ \frac{1}{\sqrt{2}} & \cos \left (\theta_{1} + \frac{2 \pi}{3} \right ) & -\sin \left (\theta_{1} + \frac{2 \pi}{3} \right ) \end{bmatrix}, \quad (\theta_{1} = \omega_{1} t) \tag{7}$

と書けます。このとき，三相座標系とd-q座標系の変換は次式のように書けます。

$\begin{bmatrix} v_{a} \\ v_{b} \\ v_{c} \end{bmatrix} = [ C ] \begin{bmatrix} v_{0} \\ v_{d} \\ v_{q} \end{bmatrix}, \quad \begin{bmatrix} i_{a} \\ i_{b} \\ i_{c} \end{bmatrix} = [ C ] \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} \tag{8}$

ここで，(6)式の中の三相座標系で書かれた電圧・電流をd-q座標系に置き換えると，

$[ C ] \begin{bmatrix} v_{0} \\ v_{d} \\ v_{q} \end{bmatrix} = R [ C ] \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} + L \displaystyle \frac{d}{dt} [ C ] \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} \tag{9}$

と表すことができ，(9)式の両辺に左から[C]⁻¹を掛けると，

$\begin{bmatrix} v_{0} \\ v_{d} \\ v_{q} \end{bmatrix} = R \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} + [ C ]^{-1} L \displaystyle \frac{d}{dt} [ C ] \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} \tag{10}$

となります。(10)式を見ると，静的な要素である抵抗Rについては[C]⁻¹と[C]が即座に打ち消しあうため，三相座標系でもd-q座標系でも変わりません。一方，動的な要素であるインダクタンスLは，行列[C]それ自身にも時間変化する量(cos θ₁, sin θ₁)を含むため，[C]⁻¹と[C]が即座に打ち消しあうことができません。(10)式右辺第2項を取り出し，積の微分の公式

$\{ f(x) g(x) \}' = f'(x) g(x) + f(x) g'(x) \tag{11}$

を適用して整理すると，次式を得ます。

$[ C ]^{-1} L \displaystyle \frac{d}{dt} [ C ] \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} = L [ C ]^{-1} \left ( \frac{d}{dt} [ C ] \right ) \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} + L \displaystyle \frac{d}{dt} \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} \tag{12}$

キモは(12)式右辺第1項ですね。一方の第2項は，電流の時間微分にLを掛けていますので，普通のインダクタンスの挙動と言えそうです。(12)式右辺第1項は一見するととても複雑な計算になるように見えるのですが，実際にやってみると，

$[ C ]^{-1} \left ( \displaystyle \frac{d}{dt} [ C ] \right ) = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -\omega_{1} \\ 0 & \omega_{1} & 0 \end{bmatrix} \tag{13}$

のように非常にシンプルな結果が得られます。(13)式の結果を使って(10)式を整理し直すと，

$\begin{bmatrix} v_{0} \\ v_{d} \\ v_{q} \end{bmatrix} = R \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} + L \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -\omega_{1} \\ 0 & \omega_{1} & 0 \end{bmatrix} \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} + L \displaystyle \frac{d}{dt} \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} \tag{14}$

と書くことができます。さらに，（時間）微分演算子pを

$p = \displaystyle \frac{d}{dt} \tag{15}$

として，RやL (d/dt)を行列の中に入れ込んでしまうと，

$\begin{bmatrix} v_{0} \\ v_{d} \\ v_{q} \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & R + p L & -\omega_{1} L \\ 0 & \omega_{1} L & R + p L \end{bmatrix} \begin{bmatrix} i_{0} \\ i_{d} \\ i_{q} \end{bmatrix} \tag{16}$

となり，さらに零相成分を無視して2 × 2の行列での表現すれば，

$\begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix} = \begin{bmatrix} R + p L & -\omega_{1} L \\ \omega_{1} L & R + p L \end{bmatrix} \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} \tag{17}$

を得ます。上式をラプラス変換すれば，pとsを置き換えるだけですが，

$\begin{bmatrix} V_{d}(s) \\ V_{q}(s) \end{bmatrix} = \begin{bmatrix} R + s L & -\omega_{1} L \\ \omega_{1} L & R + s L \end{bmatrix} \begin{bmatrix} I_{d}(s) \\ I_{q}(s) \end{bmatrix} \tag{18}$

のように表現できます。図1(b)は(17)式を回路図として，また同図(c)は(18)式をブロック線図として表現したものとなります。以上をまとめると，α-β座標系でのインピーダンスZ^s(s)は

$Z^{s}(s) = \begin{bmatrix} R + s L & 0 \\ 0 & R + s L \end{bmatrix} \tag{19}$

でしたが，これをd-q座標系に移すと，

$Z(s) = \begin{bmatrix} R + s L & -\omega_{1} L \\ \omega_{1} L & R + s L \end{bmatrix} \tag{20}$

となります（Harnefors氏の論文に倣い，上付きsがないものをd-q座標系での量とします）。う～ん──💧 これ，単なるRL直列回路でもこれほど複雑な求め方なのに，LCL回路や任意のインピーダンスについて，どうやって同様の計算をするのだろうか──。 (19)式と(20)式を比較すると，対角成分はまったく変わっていません。これ，任意のインピーダンスでも同じく対角成分は変わらないのだろうか──。また，非対角成分（干渉項）はどうやって決まるのか──。

Harnefors氏の論文のエッセンス

Harnerfors氏の論文では，複素伝達関数と伝達関数行列を活用したシンプルかつ強力な表記・計算法を提案しています。d-q座標系での任意の伝達関数行列G(s)

$G(s) = \begin{bmatrix} G_{dd}(s) & -G_{qd}(s) \\ G_{dq}(s) & G_{qq}(s) \end{bmatrix} \tag{21}$

があるとします。(21)式の対角成分・非対角成分（干渉項）が

$G_{dd}(s) = G_{qq}(s) = G_{d}(s), \quad G_{qd}(s) = G_{dq} = G_{q}(s) \tag{22}$

を満足する場合（三相平衡なインピーダンスの場合，これを満足するようです），すなわち，

$G(s) = \begin{bmatrix} G_{d}(s) & -G_{q}(s) \\ G_{q}(s) & G_{d}(s) \end{bmatrix} \tag{23}$

と書ける場合，Harnefors氏の論文によれば，これを複素伝達関数G(s)

$\boldsymbol{G}(s) = G_{d}(s) + j G_{q}(s) \tag{24}$

として表現できます。行列I, Jを

$I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \quad J = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \tag{25}$

と定義すれば，(24)式を伝達関数行列に戻すには

$G(s) = G_{d}(s) I + G_{q}(s) J \tag{26}$

とします。驚くべきことに*3，複素伝達関数G(s)（(24)式）を回転座標変換（すなわちd-q変換や逆d-q変換）するには，sをs ± jω₁に置き換えるだけでよい──とHarnefors氏の論文は主張しています。インピーダンスについても電流から電圧への伝達関数と捉えることができるので同様の議論ができます。 α-β座標系でのインピーダンスZ^s(s)が

$Z^{s}(s) = \begin{bmatrix} Z^{s}(s) & 0 \\ 0 & Z^{s}(s) \end{bmatrix} \tag{27}$

と書けるとき，これをd-q座標系に移したインピーダンスは，

$Z(s) = \begin{bmatrix} Z_{d}(s) & -Z_{q}(s) \\ Z_{q}(s) & Z_{d}(s) \end{bmatrix} \tag{28}$

と書くことができて，その要素は（sも本来は複素数ですが，それをひとまず実数だと思って計算すると*4），

$\begin{align} Z_{d}(s) &= \mathrm{Re} \left [ Z^{s}(s + j \omega_{1}) \right ] \\ Z_{q}(s) &= \mathrm{Im} \left [ Z^{s}(s + j \omega_{1}) \right ] \end{align} \tag{29}$

と書けます（(29)式は(5)式の再掲です）。

以上の議論を整理すると，（三相平衡な）任意のインピーダンスの場合について，図2のように描くことができます*5。

f:id:s-inoue2010:20210426183329p:plain:w300 — 図2: 任意のインピーダンスとそのd軸，q軸等価回路，ブロック線図

なお，時間領域で伝達関数やインピーダンスを適用する場合，Harnefors氏の論文に倣いG(s)，Z(s)の代わりにsをpに置き換えてG(p)，Z(p)と書くことにします*6。

Harnefors氏の論文での三相RL直列回路のd-q変換

Harnefors氏の論文のExample 3に記載がありますが，三相RL直列回路のα-β座標系での複素伝達関数Z^s(s)は

$\boldsymbol{Z}^{s}(s) = R + s L \tag{30}$

となって，虚数単位jのついている項はありません。(30)式を角速度ω₁で回転しているd-q座標上に移すと，

$\boldsymbol{Z}(s) = \boldsymbol{Z}^{s}(s + j \omega_{1}) = R + (s + j \omega_{1}) L = R + s L + j \omega_{1} L \tag{31}$

を得ます。(26)式に基づいて伝達関数行列に戻すと，

$Z(s) = \begin{bmatrix} R + s L & -\omega_{1} L \\ \omega_{1} L & R + s L \end{bmatrix} \tag{32}$

となって，何と(20)式と一致します。非常にシンプルです。前項は何だったのか…？*7

そして何とこれが，前述のように任意の（三相平衡の）インピーダンスに適用できると書かれています。私のような凡人にはにわかには信じがたいので，三相RL直列回路よりも少し*8複雑な例として，三相LCL回路を作って自分で確認してみることにしました。

三相LCL回路の場合

三相LCL回路のα-β座標系でのインピーダンス

図3に本記事で検討する三相LCL回路を示します。インダクタL₁，L₂，キャパシタCによるLCL回路であり，それぞれに直列抵抗R₁, R₂と並列抵抗R_pが接続されています。なお，今回は送電線の漏れ抵抗を想像して並列抵抗R_pを考えましたが，LCLフィルタなどではESR (equivalent series resistance)などを想定して直列抵抗を設けても良いと思います。同様の道筋と複雑さで計算できるのではと予想します。

f:id:s-inoue2010:20210426184942p:plain:w400 — 図3: 三相LCL回路

α-β座標系でのLCL回路のインピーダンスZ^s(s)は次式で計算できます。ここでは，複素伝達関数としてボールド体で表記します。

$\boldsymbol{Z}^{s}(s) = R_{1} + s L_{1} + (R_{2} + s L_{2}) /\!/ \left ( \displaystyle \frac{1}{s C} /\!/ R_{p} \right ) \tag{33}$

ここで「//」は電気の分野ではよく使う並列演算子であり，

$a /\!/ b = \displaystyle \frac{1}{\displaystyle \frac{1}{a} + \displaystyle \frac{1}{b}} = \displaystyle \frac{ab}{a + b} \tag{34}$

です。本記事では敢えて「//」を「和分の積」に展開しません。さて，(33)式を角速度ω₁で回転しているd-q座標系に移すと，

$\begin{align} \boldsymbol{Z}(s) &= \boldsymbol{Z}^{s}(s + j \omega_{1}) \\ &= R_{1} + (s + j \omega_{1}) L_{1} \\ &+ \{ R_{2} + (s + j \omega_{1}) L_{2} \} /\!/ \left \{ \displaystyle \frac{1}{(s + j \omega_{1}) C} /\!/ R_{p} \right \} \end{align} \tag{35}$

として表現できるはずです。

SymPyの力を借りてd-q座標系へ

ラプラス演算子sをひとまず実数と見なし，(35)式の実部と虚部を取り出せば*9，三相LCL回路のインピーダンスをd-q座標系で表現できます。しかし，(35)式は思いのほか複雑で一筋縄にはいきません。そんな時はそう…数式処理ライブラリSymPyのお力添えを頂戴します。実際にSymPyで計算してみると，(35)式の実部と虚部はともにsの有理関数となります。実部の分子多項式はsの5次式，分母多項式はsの4次式となり，一方，虚部は分子・分母多項式ともにsの4次式となりました。それぞれの係数を書き出そうとするとあまりにも煩雑になるため，ひとまず次式のように書くこととします。

$Z_{d}(s) = \mathrm{Re} [ \boldsymbol{Z}(s) ] = \displaystyle \frac{A_{5} s^{5} + A_{4} s^{4} + A_{3} s^{3} + A_{2} s^{2} + A_{1} s + A_{0}}{B_{4} s^{4} + B_{3} s^{3} + B_{2} s^{2} + B_{1} s + B_{0}} \tag{36}$

$Z_{q}(s) = \mathrm{Im} [ \boldsymbol{Z}(s) ] = \displaystyle \frac{C_{4} s^{4} + C_{3} s^{3} + C_{2} s^{2} + C_{1} s + C_{0}}{D_{4} s^{4} + D_{3} s^{3} + D_{2} s^{2} + D_{1} s + D_{0}} \tag{37}$

(36)，(37)式の係数A, B, C, Dはかなり複雑になりますので付録1に示しますが，それにしても，息切れを催すような数式ですね…。

三相LCL回路のd-q座標系でのインピーダンスの対角成分Z_d(s)はα-β座標系でのインピーダンスZ^s(s)とは異なる形となりました。三相RL回路ではいずれもZ_d(s) = Z^s(s) = R + sLであったこととは対照的です。また，非対角成分（干渉項）Z_q(s)もsの関数となりました。三相RL回路ではZ_q(s) = ω₁Lとsに依存しなかったので，この点も興味深いです。

Python ソースコード

上記の計算のためのPython ソースコードを以下に示します。

import sympy as sp

# 並列演算記号'//'のオーバーライド
## 関数parallelを定義
def parallel(self, other):
    return self * other / (self + other)

## Symbol, Add, Mulのアトリビュート__floordiv__()をparallel()でオーバーライド
sp.Symbol.__floordiv__ = parallel
sp.Add.__floordiv__ = parallel
sp.Mul.__floordiv__ = parallel

# 回路要素のシンボル
R1, L1 = sp.symbols('R_1 L_1', real = True, positive = True)
R2, L2 = sp.symbols('R_2 L_2', real = True, positive = True)
C, Rp = sp.symbols('C R_p', real = True, positive = True)

# ラプラス演算子のシンボル（便宜上，real = Trueとする）
s = sp.symbols('s', real = True)

# 基本波角周波数のシンボル
omega1 = sp.symbols('omega_1', real = True)

# 静止(α-β)座標系でのインピーダンス
Zs = R1 + s * L1 + (R2 + s * L2) // (1 / (s * C) // Rp)

# 回転(d-q)座標系でのインピーダンス
Z = Zs.subs(s, (s + sp.I * omega1))

# 対角成分
Zd = sp.re(Z).simplify()

## 対角成分の式の整理
### 分子多項式の抽出
Zd_num = sp.numer(Zd).expand().collect(s)

### 分子多項式の係数
A5 = Zd_num.coeff(s, 5)
A4 = Zd_num.coeff(s, 4)
A3 = Zd_num.coeff(s, 3)
A2 = Zd_num.coeff(s, 2)
A1 = Zd_num.coeff(s, 1)
A0 = Zd_num.coeff(s, 0)

### 分母多項式の抽出
Zd_den = sp.denom(Zd).expand().collect(s)

### 分母多項式の係数
B4 = Zd_den.coeff(s, 4)
B3 = Zd_den.coeff(s, 3)
B2 = Zd_den.coeff(s, 2)
B1 = Zd_den.coeff(s, 1)
B0 = Zd_den.coeff(s, 0)

# 非対角成分（干渉項）
Zq = sp.im(Z).simplify()

## 非対角成分の式の整理
### 分子多項式の抽出
Zq_num = sp.numer(Zq).expand().collect(s)

### 分子多項式の係数
C4 = Zq_num.coeff(s, 4)
C3 = Zq_num.coeff(s, 3)
C2 = Zq_num.coeff(s, 2)
C1 = Zq_num.coeff(s, 1)
C0 = Zq_num.coeff(s, 0)

### 分母多項式の抽出
Zq_den= sp.denom(Zq).expand().collect(s)

### 分母多項式の係数
D4 = Zq_den.coeff(s, 4)
D3 = Zq_den.coeff(s, 3)
D2 = Zq_den.coeff(s, 2)
D1 = Zq_den.coeff(s, 1)
D0 = Zq_den.coeff(s, 0)

計算例

回路定数の例

ここからは，(36)，(37)式，および付録(a) ~ (q)式に回路定数の例を代入し，(36)，(37)式のボード線図（周波数特性）を描いてみたいと思います。回路定数の例として，表1を考えました。

表1: 回路定数の例

パラメータ	値
R₁	50 mΩ
L₁	0.8 mH
R₂	100 mΩ
L₂	1.6 mH
C	50 μF
R_p	1 kΩ
ω₁	2 π × 50 rad/s

インダクタL₁は本ブログの過去の記事*10に倣い0.8 mHとしましたが，L₂については同じ値だとつまらないので，2倍の1.6 mHとしました。また，本ブログの過去の記事では，抵抗R₁ = R₂ = 10 mΩでしたが，LTspiceでのFRAを容易にするため（.tran解析が速く定常状態に収束するように），R₁, R₂として若干大き目の値を考えました。さらに，共振周波数がグラフ上で見えやすくなるように，本ブログの過去の記事での静電容量C = 1, 5, 25 μFよりも若干大き目のC = 50 μFとしました。

筆者は東日本で生まれ育ったので，電力系統の周波数と言えば50 Hzです😅 角周波数ではいつもの通り2πを掛けてω₁ = 2 π × 50 rad/sです。

Lambdify

さて，数式処理ライブラリSymPyでの計算結果である(36)，(37)式，付録(a) ~ (q)式に具体的な数値を代入して計算するにはどうすればよいでしょうか？ SymPyの数式を数値計算ライブラリNumPyで取り扱えるようにすると大変便利です。そうでなければ，SymPyの出力結果を目で見ながら，数値として計算するための関数を新たに手入力しなければならなくなり，これまた気が遠くなる作業が必要です。

lambdify関数は，SymPyの数式を数値計算用の関数に変換してくれます。具体的には，以下のソースコードのように使うことができます。ここでは，まずSymPy上で各回路定数を代入し，周波数伝達関数を演算するための下地を作ります。次にlabmdifyでNumPyで取り扱うための関数Zd_lambdaとZq_lambdaを作ります。また，比較のため，α-β座標系でのインピーダンスについてもZs_lambdaを作っておきます。

import numpy as np

# 関数の定義と回路定数の代入
# 回路定数
_R1 = 50e-3 # [Ω]
_L1 = 0.8e-3 # [H]
_R2 = 100e-3 # [Ω]
_L2 = 1.6e-3 # [H]
_C = 50e-6 # [F]
_Rp = 1e3 # [Ω]
_omega1 = 2 * sp.pi * 50 # [rad/s] 

# 対角成分関数の定義(lambdify)
_Zd = Zd.subs([(R1, _R1), (L1, _L1), (R2, _R2), (L2, _L2), \
    (C, _C), (Rp, _Rp), (omega1, _omega1)])
Zd_lambda = sp.lambdify(s, _Zd, 'numpy')

# 非対角成分（干渉項）関数の定義(lambdify)
_Zq = Zq.subs([(R1, _R1), (L1, _L1), (R2, _R2), (L2, _L2), \
    (C, _C), (Rp, _Rp), (omega1, _omega1)])
Zq_lambda = sp.lambdify(s, _Zq, 'numpy')

# 静止座標系関数の定義(lambdify)
_Zs = Zs.subs([(R1, _R1), (L1, _L1), (R2, _R2), (L2, _L2), \
    (C, _C), (Rp, _Rp)])
Zs_lambda = sp.lambdify(s, _Zs, 'numpy')

こうすることで，例えば，

omega = np.logspace(0, 5, 1000)
Zd_bode = Zd_lambda(1j * omega)
Zq_bode = Zq_lambda(1j * omega)
Zs_bode = Zs_lambda(1j * omega)

のように，数値データを容易に得ることができます。ここまで来れば，各インピーダンスの周波数特性をMatplotlibで簡単にプロットできるようになります。以下，SymPyでの数式処理結果をlambdify関数で処理し，NumPyで数値計算した結果を「SymPy-NumPyでの計算結果」などと呼ぶことにします。

LTspiceによるFRA

SymPy-NumPyでの計算結果を検証するため，LTspiceでも三相LCL回路を作り，d-q座標系でFRAしてみることにしました。三相LCL回路にテスト電圧を印加して流れた電流を観測し，その振幅と位相から（インピーダンスではなく）アドミタンスを計算します*11。図4にLTspiceの回路図(schematic)を示します。また，図5に図4中で使っている単相LCL回路の階層ブロックを示します。なお，図5にはR₁, R₂, R_pがシンボルとして表れておりませんが，L₁, L₂, Cの内蔵直列抵抗，内蔵並列抵抗としてモデル化しています*12。図4では，座標変換などに筆者の自作制御ライブラリContrailleを活用しています*13。

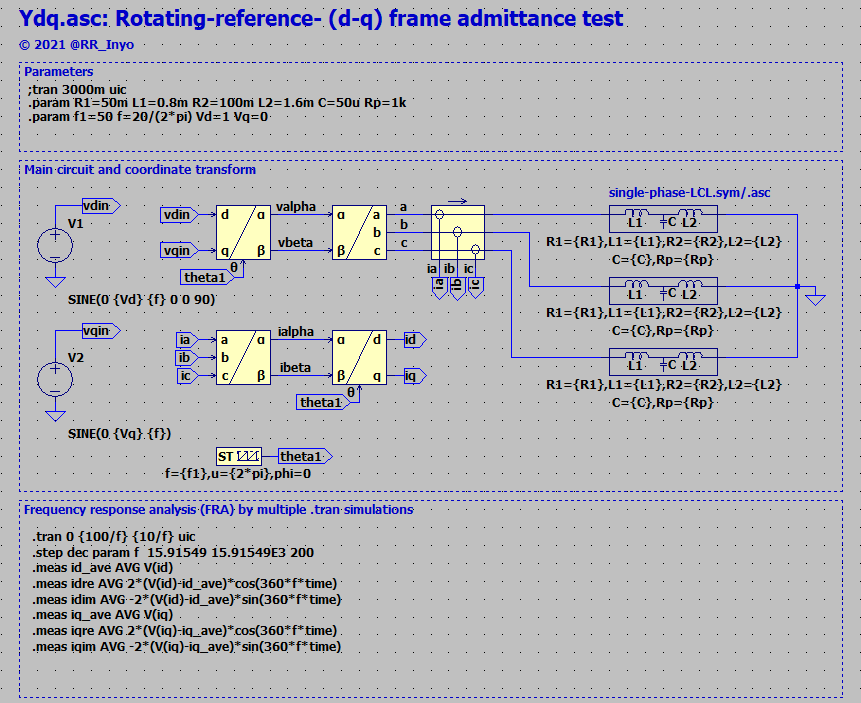
f:id:s-inoue2010:20210427032924p:plain — 図4: LTspiceによる三相LCL回路のFRAのための回路図

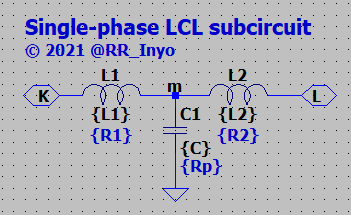
f:id:s-inoue2010:20210427033455p:plain — 図5: 単相LCL回路の階層ブロック

FRAについては本ブログの過去の記事*14でも取り扱っておりますが，簡単におさらいします。三相LCL回路に，ある周波数fの正弦波としてd-q座標系での入力電圧vdin, vqinを与えます*15。結果として流れた電流ia, ib, icをd-q座標系に移し，id, iqを得ます。得られたid, iqに含まれる周波数fの成分を.measコマンドで抽出します。また，.step paramコマンドで周波数fをスキャンしていきます。

テスト電圧であるvdin, vqinですが，ここではvdinの振幅を1 V，vqinの振幅を0 Vとします。この場合，得られたid, iqはd-q座標系でのアドミタンスの対角成分Y_d(jω)と非対角成分（干渉項）Y_q(jω)に相当します。次式のように逆行列を求めれば（シンプルな表記とするため，「(s)」や「(jω)」を省略しました），アドミタンスY(jω)とインピーダンスZ(jω)と相互変換が可能です*16。

$Y = \begin{bmatrix} Y_{d} & -Y_{q} \\ Y_{q} & Y_{d} \end{bmatrix} = \begin{bmatrix} Z_{d} & -Z_{q} \\ Z_{q} & Z_{d} \end{bmatrix}^{-1} = \displaystyle \frac{1}{Z_{d}^{2} + Z_{q}^{2}} \begin{bmatrix} Z_{d} & Z_{q} \\ -Z_{q} & Z_{d} \end{bmatrix} \tag{38}$

$Z = \begin{bmatrix} Z_{d} & -Z_{q} \\ Z_{q} & Z_{d} \end{bmatrix} = \begin{bmatrix} Y_{d} & -Y_{q} \\ Y_{q} & Y_{d} \end{bmatrix}^{-1} = \displaystyle \frac{1}{Y_{d}^{2} + Y_{q}^{2}} \begin{bmatrix} Y_{d} & Y_{q} \\ -Y_{q} & Y_{d} \end{bmatrix} \tag{39}$

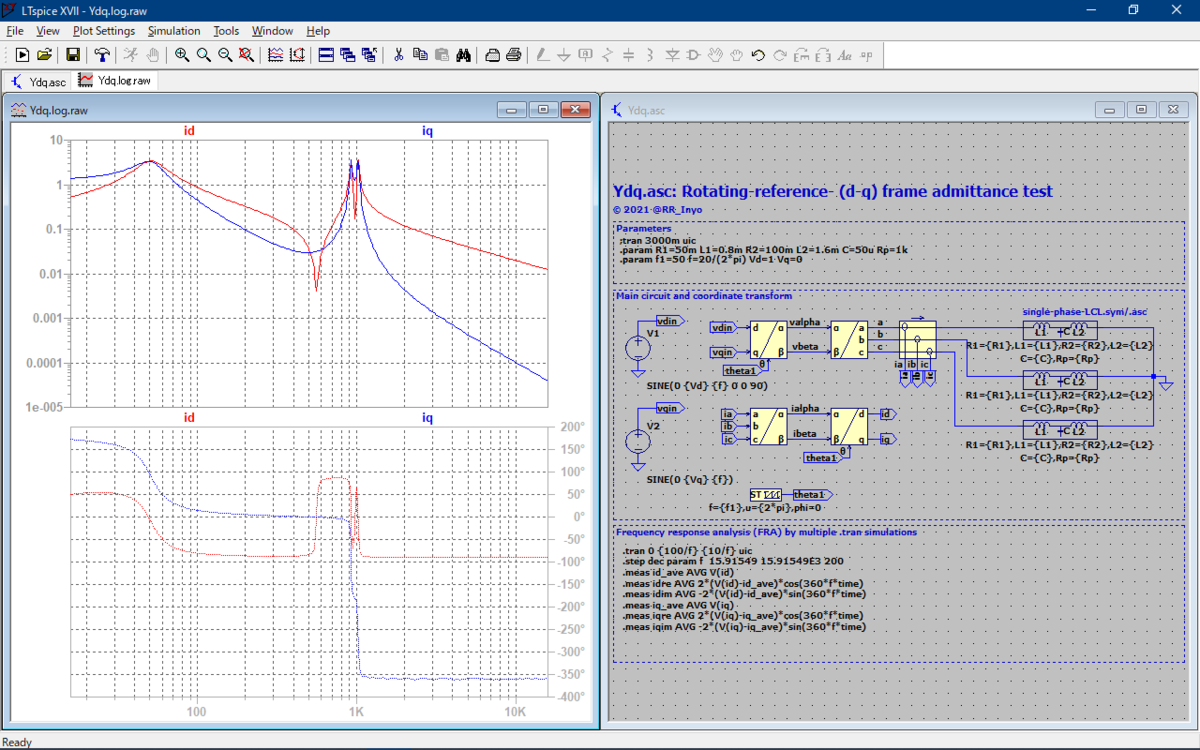
f:id:s-inoue2010:20210427102449p:plain — 図6: LTspiceでのFRAの様子

図6にLTspiceでのFRAの様子を示します。601ステップの計算となりましたが，今回はスイッチング回路ではないので10分ほどで計算が完了しました。

計算結果

図7，8に三相LCL回路のd-q座標系におけるインピーダンスを計算した結果を示します。図8は図7における共振周波数付近での拡大図です（横軸はリニアになっています）。

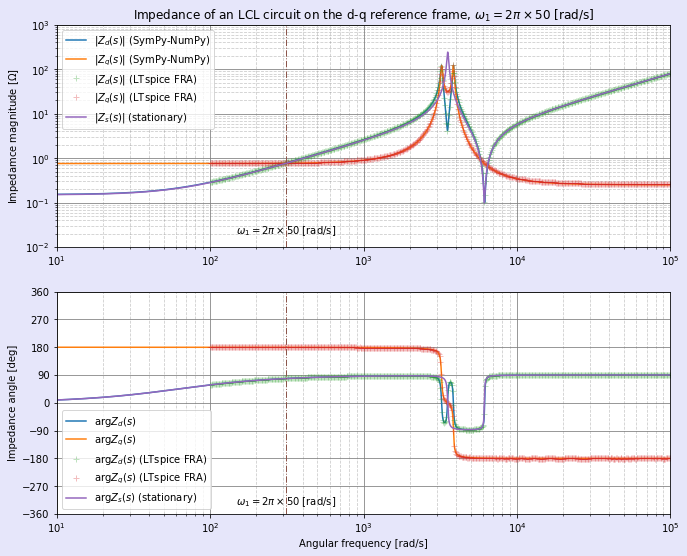
f:id:s-inoue2010:20210427083827p:plain — 図7: 三相LCL回路のd-q座標系でのインピーダンスの計算結果

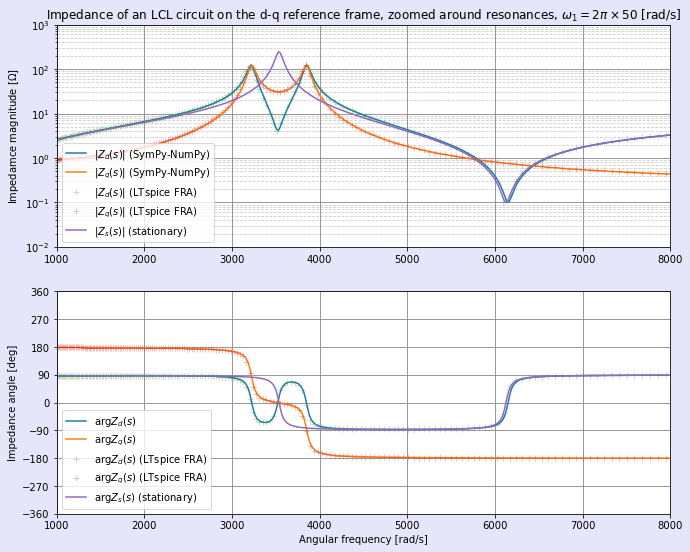
f:id:s-inoue2010:20210427083911p:plain — 図8: 図7の共振周波数付近の拡大図

青色と橙色の実線がSymPy-NumPyによる計算結果のプロットであり，青が対角成分Z_d(jω)，橙が非対角成分（干渉項）Z_q(jω)です。また，紫色の実線は静止(α-β)座標系でのインピーダンスのプロットです。さらに，「+」印にてLTspiceによるFRAの結果をプロットしています。SymPy-NumPyでの計算結果はLTspiceによるFRAとほぼ完全に一致しており，数式ベースでの検討が正しいことを確認できました。

α-β座標系でのインピーダンスZ^s(jω)とd-q座標系でのインピーダンスの対角成分Z_d(jω)は低周波や高周波では概ね一致していますが，共振周波数付近では不一致が大きくなります（三相RL直列回路では前述の通り完全に一致します）。特に，筆者は理論的背景をまだ理解できていませんが，並列共振点ではZ_d(jω)の山が2つに割れます。また，非対角成分（干渉項）は同じ周波数で並列共振となりますが，直列共振点を持たないようです。三相LCL回路のインピーダンスについては，d-q座標系の回転角周波数であるω₁付近で特にピークが出たりはしないようです。

図9，10に，三相LCL回路のd-q座標系におけるアドミタンスの計算結果を示します。図9は図8における共振周波数付近での拡大図です（横軸はリニアになっています）。

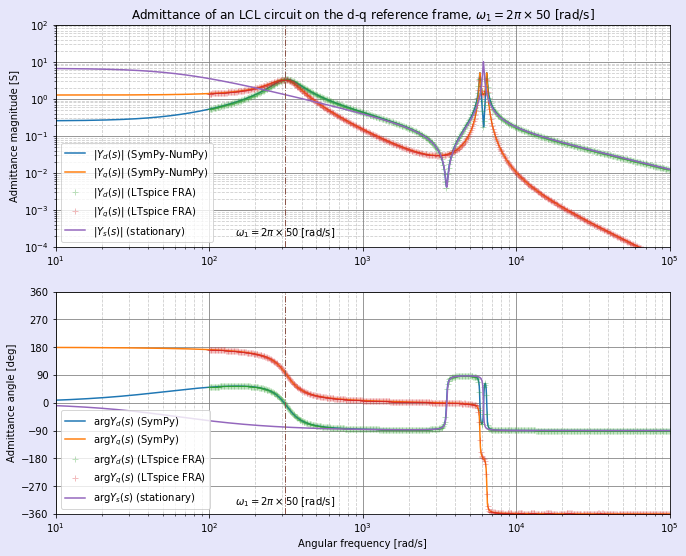
f:id:s-inoue2010:20210427134919p:plain — 図9: 三相LCL回路のd-q座標系におけるアドミタンスの計算結果

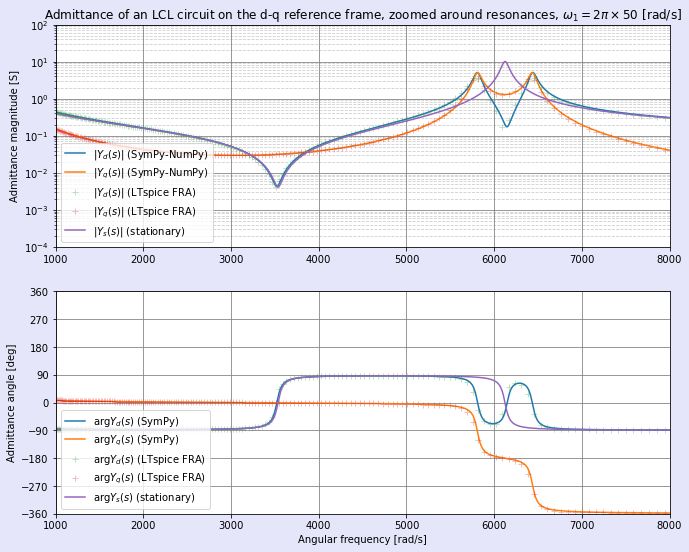
f:id:s-inoue2010:20210427083843p:plain — 図10: 図9の共振周波数付近の拡大図

アドミタンスについては，d-q座標系の回転角周波数であるω₁付近でピークが出ています。一方，α-β座標系でのアドミタンスにはピークはありません。共振周波数付近の挙動は，図7，図8と反転したような形になっていることが分かります。

まとめ

本記事では，三相LCL回路のd-q座標系におけるインピーダンスを求めるために，まず三相RL直列回路の場合をおさらいした後，任意のインピーダンスをd-q座標系に移すための手法を提案しているHarnefors氏の論文のエッセンスを紹介しました。その後，その手法に基づいて三相LCL回路のインピーダンスを実際にd-q座標系に移す計算を試みました。本ブログの常套手段ですが，思いのほか数式が煩雑であったため，数式処理ライブラリSymPyからの援軍に頼りました。また，lambdify関数を使って，SymPyの数式を数値計算ライブラリNumPyで用いる方法を試みました。さらに，SymPy-NumPyの合わせ技によって得られた結果を，LTspiceによる周波数スキャン(FRA)と比較し，一致することを確認しました。

今回は三相LCL回路を例としましたが，回路トポロジーと回路定数が既知であれば，どのようなインピーダンスでもd-q座標系に移すことができそうです。もちろん，数式が加速度的に複雑になっていくため，SymPyの力が欠かせません。しかし，方法論としては共通です。求めたd-q座標系でのインピーダンスは，三相系統連系インバータの安定性の解析などに役に立つのではないかと考えます。

今後の議論

Z^s(jω)の数値データからZ_d(jω)，Z_q(jω)を得られるか

さて，本記事では回路構成が三相LCL回路であること，そしてその回路定数も既知でした。したがって，Z^s(s)の数式表現が得られていました。一方，もし，Z^s(s)のトポロジーや回路定数が分からず，したがって数式表現が未知であり，例えばインピーダンスアナライザでの測定結果のようにZ^s(jω)の数値データだけが手元にあった場合，これを使ってd-q座標系でのインピーダンスZ_d(jω)，Z_q(jω)を（近似でもよいので）得ることはできるでしょうか？今のところの筆者の理解では，これは難しいのではないかと考えています。システム同定の手法を使って，Z^s(jω)の数値データから数式表現を得るしかないように見えます。

不平衡な場合

Harnefors氏の論文には三相不平衡な場合についても記載があります。また，Harnefors氏の論文に引用されたり，同論文を引用したりしている関連文献がIEEEでは思いのほか多くpublishされています*17。本記事では系統側のインピーダンス（ほぼ三相平衡と見なせるでしょう）を取り扱いましたが，三相不平衡になると思われるインバータ側のインピーダンスについても筆者自身の中に理解と計算方法を確立していきたいと考えています。

付録1: 係数A, B, C, D

(36)，(37)式の分子・分母多項式の係数A, B, C, Dを具体的に書き出します。

$A_{5} = C^{2} L_{1} L_{2}^{2} R_{p}^{2} \tag{a}$

$A_{4} = 2 C^{2} L_{1} L_{2} R_{2} R_{p}^{2} + C^{2} L_{2}^{2} R_{1} R_{p}^{2} + 2 C L_{1} L_{2}^{2} R_{p} \tag{b}$

$\begin{align} A_{3} &= 2 C^{2} L_{1} L_{2}^{2} R_{p}^{2} \omega_{1}^{2} + C^{2} L_{1} R_{2}^{2} R_{p}^{2} + 2 C^{2} L_{2} R_{1} R_{2} R_{p}^{2} \\ &+ 4 C L_{1} L_{2} R_{2} R_{p} + 2 C L_{1} L_{2} R_{p}^{2} + 2 C L_{2}^{2} R_{1} R_{p} \\ &+ C L_{2}^{2} R_{p}^{2} + L_{1} L_{2}^{2} \end{align} \tag{c}$

$\begin{align} A_{2} &= 2 C^{2} L_{1} L_{2} R_{2} R_{p}^{2} \omega_{1}^{2} + 2 C^{2} L_{2}^{2} R_{1} R_{p}^{2} \omega_{1}^{2} + C^{2} R_{1} R_{2}^{2} R_{p}^{2} \\ &+ 2 C L_{1} L_{2}^{2} R_{p} \omega_{1}^{2} + 2 C L_{1} R_{2}^{2} R_{p} + 2 C L_{1} R_{2} R_{p}^{2} \\ &+ 4 C L_{2} R_{1} R_{2} R_{p} + 2 C L_{2} R_{1} R_{p}^{2} + 2 C L_{2} R_{2} R_{p}^{2} \\ &+ 2 L_{1} L_{2} R_{2} + 2 L_{1} L_{2} R_{p} + L_{2}^{2} R_{1} \\ &+ L_{2}^{2} R_{p} \end{align} \tag{d}$

$\begin{align} A_{1} &= C^{2} L_{1} L_{2}^{2} R_{p}^{2} \omega_{1}^{4} + C^{2} L_{1} R_{2}^{2} R_{p}^{2} \omega_{1}^{2} + 2 C^{2} L_{2} R_{1} R_{2} R_{p}^{2} \omega_{1}^{2} \\ &- 2 C L_{1} L_{2} R_{p}^{2} \omega_{1}^{2} + 2 C L_{2}^{2} R_{1} R_{p} \omega_{1}^{2} + C L_{2}^{2} R_{p}^{2} \omega_{1}^{2} \\ &+ 2 C R_{1} R_{2}^{2} R_{p} + 2 C R_{1} R_{2} R_{p}^{2} + C R_{2}^{2} R_{p}^{2} \\ &+ L_{1} L_{2}^{2} \omega_{1}^{2} + L_{1} R_{2}^{2} + 2 L_{1} R_{2} R_{p} \\ &+ L_{1} R_{p}^{2} + 2 L_{2} R_{1} R_{2} + 2 L_{2} R_{1} R_{p} \\ &+ 2 L_{2} R_{2} R_{p} + L_{2} R_{p}^{2} \end{align} \tag{e}$

$\begin{align} A_{0} &= C^{2} L_{2}^{2} R_{1} R_{p}^{2} \omega_{1}^{4} + C^{2} R_{1} R_{2}^{2} R_{p}^{2} \omega_{1}^{2} - 2 C L_{2} R_{1} R_{p}^{2} \omega_{1}^{2} \\ &+ L_{2}^{2} R_{1} \omega_{1}^{2} + L_{2}^{2} R_{p} \omega_{1}^{2} + R_{1} R_{2}^{2} \\ &+ 2 R_{1} R_{2} R_{p} + R_{1} R_{p}^{2} + R_{2}^{2} R_{p} \\ &+ R_{2} R_{p}^{2} \end{align} \tag{f}$

$B_{4} = C^{2} L_{2}^{2} R_{p}^{2} \tag{g}$

$B_{3} =2 C^{2} L_{2} R_{2} R_{p}^{2} + 2 C L_{2}^{2} R_{p} \tag{h}$

$\begin{align} B_{2} &= 2 C^{2} L_{2}^{2} R_{p}^{2} \omega_{1}^{2} + C^{2} R_{2}^{2} R_{p}^{2} + 4 C L_{2} R_{2} R_{p} \\ &+ 2 C L_{2} R_{p}^{2} + L_{2}^{2} \end{align} \tag{i}$

$\begin{align} B_{1} &= 2 C^{2} L_{2} R_{2} R_{p}^{2} \omega_{1}^{2} + 2 C L_{2}^{2} R_{p} \omega_{1}^{2} + 2 C R_{2}^{2} R_{p} \\ &+ 2 C R_{2} R_{p}^{2} + 2 L_{2} R_{2} + 2 L_{2} R_{p} \end{align} \tag{j}$

$\begin{align} B_{0} &= C^{2} L_{2}^{2} R_{p}^{2} \omega_{1}^{4} + C^{2} R_{2}^{2} R_{p}^{2} \omega_{1}^{2} - 2 C L_{2} R_{p}^{2} \omega_{1}^{2} \\ &+ L_{2}^{2} \omega_{1}^{2} + R_{2}^{2} + 2 R_{2} R_{p} \\ &+ R_{p}^{2} \end{align} \tag{k}$

$C_{4} = C^{2} L_{1} L_{2}^{2} R_{p}^{2} \omega_{1} \tag{l}$

$C_{3} = 2 C^{2} L_{1} L_{2} R_{2} R_{p}^{2} \omega_{1} + 2 C L_{1} L_{2}^{2} R_{p} \omega_{1} \tag{m}$

$\begin{align} C_{2} &= 2 C^{2} L_{1} L_{2}^{2} R_{p}^{2} \omega_{1}^{3} + C^{2} L_{1} R_{2}^{2} R_{p}^{2} \omega_{1} + 4 C L_{1} L_{2} R_{2} R_{p} \omega_{1} \\ &+ 2 C L_{1} L_{2} R_{p}^{2} \omega_{1} - C L_{2}^{2} R_{p}^{2} \omega_{1} + L_{1} L_{2}^{2} \omega_{1} \end{align} \tag{n}$

$\begin{align} C_{1} & = C^{2} L_{2}^{2} R_{1} R_{p}^{2} \omega_{1}^{4} + C^{2} R_{1} R_{2}^{2} R_{p}^{2} \omega_{1}^{2} - 2 C L_{2} R_{1} R_{p}^{2} \omega_{1}^{2} \\ &+ L_{2}^{2} R_{1} \omega_{1}^{2} + L_{2}^{2} R_{p} \omega_{1}^{2} + R_{1} R_{2}^{2} \\ &+ 2 R_{1} R_{2} R_{p} + R_{1} R_{p}^{2} + R_{2}^{2} R_{p} \\ &+ R_{2} R_{p}^{2} \end{align} \tag{o}$

$\begin{align} C_{0} & = C^{2} L_{1} L_{2}^{2} R_{p}^{2} \omega_{1}^{5} + C^{2} L_{1} R_{2}^{2} R_{p}^{2} \omega_{1}^{3} - 2 C L_{1} L_{2} R_{p}^{2} \omega_{1}^{3} \\ &- C L_{2}^{2} R_{p}^{2} \omega_{1}^{3} - C R_{2}^{2} R_{p}^{2} \omega_{1} + L_{1} L_{2}^{2} \omega_{1}^{3} \\ &+ L_{1} R_{2}^{2} \omega_{1} + 2 L_{1} R_{2} R_{p} \omega_{1} + L_{1} R_{p}^{2} \omega_{1} \\ &+ L_{2} R_{p}^{2} \omega_{1} \end{align} \tag{p}$

$D_{k} = B_{k}, \quad (k = 0, 1, 2, 3, 4) \tag{q}$

付録2: 三相RL直列回路においてα-β座標系での表現を出発点とした場合

三相座標系での表現である(6)式を出発点とした場合，三相座標系からα-β座標系への変換が加わるので，本記事では必要以上に複雑に見えてしまったかもしれません。その前に，(2)，(3)式で説明したように，相間の干渉（相互インダクタンスなど）がなければ，三相座標系とα-β座標系でのインピーダンスは一致します。そこで，

$\begin{bmatrix} v_{\alpha} \\ v_{\beta} \end{bmatrix} = R \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix} + L \displaystyle \frac{d}{dt} \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix} \tag{i}$

を出発点として書き直してみます。逆d-q変換に相当する行列を[C_dq]とすると，

$[ C_{dq} ] = \begin{bmatrix} \cos \theta_{1} & -\sin \theta_{1} \\ \sin \theta_{1} & \cos \theta_{1} \end{bmatrix}, \quad (\theta_{1} = \omega_{1} t) \tag{ii}$

となります。また，(ii)式を用いると，電圧と電流について，

$\begin{bmatrix} v_{\alpha} \\ v_{\beta} \end{bmatrix} = [C_{dq} ] \begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix}, \quad \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix} = [ C_{dq} ] \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} \tag{iii}$

と書けますので，これを(i)式に代入して

$[ C_{dq} ] \begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix} = R [ C_{dq} ] \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} + L \displaystyle \frac{d}{dt} [ C_{dq} ] \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} \tag{iv}$

となります。さらに，(iv)式に左から[C_dq]⁻¹を掛けて，

$\begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix} = R \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} + [ C_{dq} ]^{-1} L \displaystyle \frac{d}{dt} [ C_{dq} ] \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} \tag{v}$

となります。やはり，静的な要素であるRについては，[C_dq]⁻¹と[C_dq]が即座に打ち消しあいますが，動特性をもつLについてはそうはいきません。積の微分の公式である(11)式を用いて(v)式右辺第2項を整理すると，

$[ C_{dq} ]^{-1} L \displaystyle \frac{d}{dt} [ C_{dq} ] \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} = L [ C_{dq} ]^{-1} \left ( \displaystyle \frac{d}{dt} [ C_{dq} ] \right ) \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} + L \displaystyle \frac{d}{dt} \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} \tag{vi}$

となります。(vi)式右辺第2項は電流の時間微分にLを掛けていますので，普通のインダクタンスの挙動ですね。もう一方，第1項を実際に微分してみると，

$\displaystyle \frac{d}{dt} [ C_{dq} ] = \displaystyle \frac{d}{dt} \begin{bmatrix} \cos \theta_{1} & -\sin \theta_{1} \\ \sin \theta_{1} & \cos \theta_{1} \end{bmatrix} = \begin{bmatrix} -\omega_{1} \sin \theta_{1} & -\omega_{1} \cos \theta_{1} \\ \omega_{1}\cos \theta_{1} & -\omega_{1} \sin \theta_{1} \end{bmatrix} \tag{vii}$

となります。[C_dq]の逆行列[C_dq]⁻¹については，非対角成分の符号を入れ替えるだけですので，次式となります。

$[ C_{dq} ] ^{-1} = \begin{bmatrix} \cos \theta_{1} & \sin \theta_{1} \\ -\sin \theta_{1} & \cos \theta_{1} \end{bmatrix}, \quad (\theta_{1} = \omega_{1} t) \tag{viii}$

したがって，

$\begin{align} [ C_{dq} ]^{-1} \displaystyle \frac{d}{dt} [ C_{dq} ] &= \begin{bmatrix} \cos \theta_{1} & \sin \theta_{1} \\ -\sin \theta_{1} & \cos \theta_{1} \end{bmatrix} \begin{bmatrix} -\omega_{1} \sin \theta_{1} & -\omega_{1} \cos \theta_{1} \\ \omega_{1}\cos \theta_{1} & -\omega_{1} \sin \theta_{1} \end{bmatrix} \\ &= \begin{bmatrix} 0 & -\omega_{1} \\ \omega_{1} & 0 \end{bmatrix} \end{align}\tag{ix}$

とシンプルな形に落ち着きます。(ix)式を用いて(vi)式を整理し直すと

$\begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix} = R \begin{bmatrix} i_{d} \\ i_{d} \end{bmatrix} + L \begin{bmatrix} 0 & -\omega_{1} \\ \omega_{1} & 0 \end{bmatrix} \begin{bmatrix} i_{d} \\ i_{d} \end{bmatrix} + L \displaystyle \frac{d}{dt} \begin{bmatrix} i_{d} \\ i_{d} \end{bmatrix} \tag{x}$

となります。（時間）微分演算子p = d/dtをおき，RとL (d/dt)を行列の中に入れ込むと，

$\begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix} = \begin{bmatrix} R + p L & -\omega_{1} L \\ \omega_{1} L & R + p L \end{bmatrix} \begin{bmatrix} i_{d} \\ i_{d} \end{bmatrix} \tag{xi}$

と書くことができます。(xi)式をラプラス変換すれば，pをsに置き換えるだけですが，

$\begin{bmatrix} V_{d}(s) \\ V_{q}(s) \end{bmatrix} = \begin{bmatrix} R + s L & -\omega_{1} L \\ \omega_{1} L & R + s L \end{bmatrix} \begin{bmatrix} I_{d}(s) \\ I_{q}(s) \end{bmatrix} \tag{xii}$

と書くことができます。これは(18)式に一致します。

*1:LTspiceで三相PWM整流器を作る～d-q座標系編～ - The Negligible Lab

*2:慣習的に多くの教科書で「逆」変換の行列を[C]として扱っています。

*3:私の頭が悪いだけ？

*4:筆者の浅薄な理解では，Harnefors氏の論文には巧い記号が設けられていないようでした。

*5:ただし，簡単のため相互インピーダンスが零の場合を例示しています。相互インピーダンスがあっても，α-β座標系でのインピーダンスの非対角成分が零であれば議論の内容は変わりません。

*6:s領域で入力をU(s)，出力をY(s)としてY(s) = G(s) U(s)と書ける場合，これを時間領域に置き換えると，Harnefors氏の論文では便宜的にy(t) = G(p) u(t)と書いています。本来，時間領域での出力y(t)は，G(s)のインパルス応答g(t) = ℒ⁻¹[G(s)]と入力u(t)の畳み込み積分∫ g(τ − t) y(τ) dτですので，y(t) = G(p) u(t)という表記はこれを略記したものと理解しています。原文では，“The derivative operator p = d/dt is substituted for the Laplace variable s whenever a transfer function or matrix is used as an operator.”，と脚注に書かれています。

*7:三相座標系ではなくα-β座標系を出発点にしていることも単純さの要因かもしれません。α-β座標系を出発点にした式展開を付録2に示します。

*8:すぐ後に出てきますが，「少し」じゃなかった…。

*9:もう少しきちんとした言い方をすれば，「jの1次の係数と0次の係数を抽出すれば」と言えるかもしれません。

*10:系統連系インバータの電流制御と系統インピーダンス - The Negligible Lab

*11:インピーダンスを直接求めるにはテスト電流を注入する必要があります。しかし，LCL回路なのでその端部にあるインダクタに電流源を接続すると計算が収束しにくくなるかと考え，テスト電圧を印加してアドミタンスを求めることとしました。インピーダンスは(38)，(39)式のように逆行列の計算で求まります。

*12:LTspiceではLやCの直並列抵抗を個別のシンボルとせず，内蔵（寄生）抵抗としてモデル化した方が高速な計算が可能とのことです。LTspiceのヘルプをご参照下さい。

*13:LTspice用制御ライブラリContraille ～概要編～ - The Negligible Lab

*14:移動平均フィルタとサンプル & ホールド - The Negligible Lab

*15:d-q座標系で正弦波という点がミソです。三相座標系での電圧は周波数fと基本波周波数50 Hzが混合した複雑な波形となります。

*16:当初，Z_d(jω) = 1 / Y_d(jω)だと単純に思い込んで計算してしまい（頭悪すぎ…），SymPy-NumPyがLTspice-FRAと合わないと悩んでいました💧

*17:日本の電気学会では系統連系インバータの安定性を取り扱っている論文は少ないように見えますね。あくまで個人の感想ですが，モータドライブ技術の研究者の方々は制御技術にも明るいと思われますので，本記事の内容もひょっとすると常識なのかもしれません。