The Negligible Lab

Astray in the forest of electrical and electronic circuits. Adrift in the gap between time and frequency domains. 独立独歩を是とする。

Pythonによる車輪のシミュレーションとアニメーション

制御工学 Python JupyterLab SciPy Matplotlib

はじめに

P計画

2023年を迎えて2月に入り，その2月も終盤に差し掛かろうとしています。三寒四温──もう春が近いですね…🌸 筆者が年初に思い描いた目標の1つに「車輪形倒立振子を作る」があります。ESP32等のマイコンモジュールとMPU6050等のジャイロセンサ，モータドライバIC，DCモータと車輪を組み合わせれば，ハードウェアとしては（拙いながらも）作ることだけはできそうです。実際，昨年に荒い試作をしてみましたが，残念ながら倒立する気配はありませんでした。

やはり，まずは数理モデルを構築し，現代制御理論に立脚した制御設計を経てこそ，倒立振子の真の醍醐味を得られるのではないか──？

このような訳で，いきなり実機を作ることはやめ，まずはシミュレータを作ろうと思い立ちました。と言っても，いきなり車輪形倒立振子全体のシミュレータを作るのはハードルが高い，また，車輪形倒立振子の出来上がった運動方程式を他所からコピー & ペーストしてきても勉強にならないので，数学弱者たる筆者が理解できる範囲を少しずつ広げるため，段階を追うことにしました。

図1: トルクを与えられて回転する車輪のアニメーション

まず今回は，トルクを与えられて床面を転がる車輪をモデル化し，シミュレーション，そして可視化のためにアニメーションを作ることにします。上の図1が完成したアニメーションになります。次回以降，振り子やDCモータなどにモデル化の範囲を広げていき（途中で台車形倒立振子のシミュレータも作ります），最終的には車輪形倒立振子のシミュレーション，アニメーションを作り，実機の設計に繋げていきます。

科学計算ツール

「トランジスタ技術」2020年7月号の記事（参考文献1）にて早川槙一さんがLTspiceを使った車輪形倒立振子のシミュレータを構築し，かつ，OPアンプによるアナログ制御を実現するという刺激的な挑戦をされていました。これを拝読したときから，筆者の中で倒立振子を作ろうという機運が高まってきたと言えます。技術者のはしくれとして，倒立振子ぐらい立たせたいではないか！

筆者もLTspiceの取り扱いにはある程度慣れているつもりですが，LTspiceでは時間波形の表示しかできず，車輪なり倒立振子なりが動いている様子をアニメーションさせることはできません。やはり目で見て楽しい（！）シミュレータを目指したいので，微分方程式（運動方程式）の求解とアニメーションをPython*1で組んでみることにしました*2。

この分野には優れた先賢たちが幾多の書籍，論文，ウェブサイト，ブログ記事，動画などに記録を残しているため，本記事が何か新しいことを提供できているかは不明ですが，ひとまず続けていこうと思います。

Jupyter Notebook

本記事のために作成したJupyter NotebookをGitHubに置きました。適宜ご参照下さい。

github.com

目次

車輪のモデル

運動方程式

図2に今回の対象となる車輪のモデルを示します。 床の上に半径a，質量M，慣性モーメントJの車輪が置かれており，車輪が床と接する点のx座標をxwとすることにします。また，（手段は特定しませんが）トルクτを与えられて回転し，床を転がります。車輪の重心の速度をvwとし，回転の角速度をωとします。さらに，角度θに関しては，車輪がx軸の正方向に進む時計回りを正とし，車輪の接地点がx軸の原点にあるときにθ = 0とすることにしました。

図2: 車輪のモデル

車輪の接地点には床面からの摩擦力が加わりますが，これをひとまずfと書くことにします*3。

さて，車輪の重心の並進運動と，重心の周りの回転運動に関する運動方程式を書き出せば，

\begin{align} M \dot{v}_{w} &= f \\[10pt] J \dot{\omega} &= \tau - f a \end{align} \tag{1}

を得ます。ここで

\dot{v}_{w} = \ddot{x}_{w}, \quad \dot{\omega} = \ddot{\theta} \tag{2}

です。簡潔なので，以後は時間微分に関してニュートンのドット記法を基本としますが，図中など必要に応じてライプニッツの記法も用います。

摩擦力fとは？ ～ 並進と回転を1つの式に集約 ～

さて，摩擦力fとは何でしょうか？ 結論から言えば，車輪が滑らないという拘束条件の下ではこれは静止摩擦力であり，その大きさは可変です。筆者はこれがよく分からずにしばらく悩んでしまいました。すると，Twitterにて有識者の方から的確なアドバイスを頂き，また，東京図書の力学の教科書（参考文献2）を眺めていると，ようやくイメージが湧いてきました。

先の図2では図示を省略した力があります。そう，図3に示すように，車輪に鉛直下向きに働く重力と，それに対する床面からの垂直抗力です。これらはともに大きさMgで逆向きとなるため打ち消し合います。したがって，（車輪が床から離れない・ジャンプしないという条件下で）運動に影響は与えませんが，床からの垂直抗力は車輪の接地点に対して働く摩擦力fを生みます。

図3: 重力・抗力・静止摩擦力

この摩擦力fは車輪が滑らないとすれば静止摩擦力です。静止摩擦力の最大値は静止摩擦係数と垂直抗力の積で決まりますが，静止摩擦力のその時の大きさは，車輪が滑らないという拘束条件で決まります。

ここで，「車輪が滑らない」とは，「車輪の接地点の速度が常に零になる」という意味です。言い換えると，車輪の周速と車輪の重心の速さが等しくなるということですね。これを数式で書けば，

a \omega = v_{w} \quad \left (\therefore \dot{\omega} = \displaystyle \frac{\dot{v}_{w}}{a} \right ) \tag{3}

となります。これを(1)式に代入すると摩擦力fを消去することができ，\dot{v}_{w}のみの式に書き直せば，

\dot{v}_{w} = \displaystyle \frac{\tau}{M a + \displaystyle \frac{J}{a}} \tag{4}

という運動方程式を得ます。また，状態変数として，

\boldsymbol{x}(t) = [x_{w}(t), v_{w}(t) ]^{T} \tag{5}

を採れば，

\begin{bmatrix} \dot{x}_{w} \\[5pt] \dot{v}_{w} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\[5pt] 0 & 0 \end{bmatrix} \begin{bmatrix} x_{w} \\[5pt] v_{w} \end{bmatrix} + \begin{bmatrix} 0 \\[5pt] \displaystyle \frac{1}{M a + \displaystyle \frac{J}{a}} \end{bmatrix} \tau \tag{7}

のような状態方程式として書くこともできますね。ここで，車輪が円板であるとすると，慣性モーメントJに関して

J = \displaystyle \frac{1}{2} M a^{2} \tag{8}

となりますので，これを(7)式に代入すれば，

\begin{bmatrix} \dot{x}_{w} \\[5pt] \dot{v}_{w} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\[5pt] 0 & 0 \end{bmatrix} \begin{bmatrix} x_{w} \\[5pt] v_{w} \end{bmatrix} + \begin{bmatrix} 0 \\[5pt] \displaystyle \frac{2}{3 M} \end{bmatrix} \tau \tag{8}

と書くこともできます。これは単に，質量M' = 3 M / 2の物体を摩擦のない面で（滑って）動かしている運動方程式（状態方程式）となります。トルクτによるエネルギーが車輪（円板）の並進と回転の双方に分配されるため，並進だけに着目すると質量が1.5倍になったように見えている訳です。

ここまでは筆者による力学の学び直しとなります*4。

scipy.integrate.solve_ivp関数の使い方

2階定数係数線形常微分方程式の一例とそのPythonでの表現

ここではいきなり上述の車輪を扱わず，まずは，微分方程式の初期値問題の求解に使えるscipy.integrate.solve_ivp関数*5の使い方を簡単にご説明します。公式ドキュメントは下記となります（“ivp”とはinitial-value problemの略でしょうか）。

docs.scipy.org

以下のように各ライブラリ・モジュールがインポートされているものとします。

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
import matplotlib.patches as patches

ここでは例として2階定数係数線形常微分方程式

\ddot{x} + \dot{x} + 5 x - 4 = 0 \tag{9}

を考えましょう*6。これを1階の連立微分方程式に書き直します。

\begin{align} \displaystyle \frac{d}{dt} x &= \dot{x} \\[5pt] \displaystyle \frac{d}{dt} \dot{x} &= -5 x - \dot{x} + 4 \end{align} \tag{10}

solve_ivp関数でこれを解く場合，(10)式をPythonの関数として以下のように書き表します。ただし，状態変数を

\boldsymbol{y}(t) = [x(t), \dot{x}(t)]^{T} \tag{11}

とします。

def func(t, y):
    dydt = np.zeros_like(y)
    dydt[0] = y[1]
    dydt[1] = -5 * y[0] - y[1] + 4
    return dydt

2行目では，引数として与えられた状態変数\boldsymbol{y}(t)に相当するyと同じ大きさで中身が零のNumPyの配列dydtを生成します。その後の2行で(10)式に相当する連立微分方程式を記述しています。最後に中身を入れ込んだdydtを返します。要するに，時刻tと現在の状態\boldsymbol{y}(t)を与えられて時間微分係数\dot{\boldsymbol{y}}(t)を返す訳です。まさに微分方程式ですね。

初期値問題を解く

さて，初期値x(0) = 0，\dot{x}(0) = 0すなわち\boldsymbol{y}_{0}= [0, 0]^{T}として初期値問題を解く場合，下記のように記述します。

t_span = [0, 10]
t = np.arange(0, 10, 0.01)
y0 = [0, 0]
sol = solve_ivp(func, t_span, y0, t_eval = t)

キモとなるのは最後のsolve_ivp関数となり，返り値として解solを得ることができます。ここで使用したsolve_ivp関数の引数は表1のようになります。

表1: solve_ivp関数の引数

引数意味
func微分方程式を表す関数
t_span数値積分を計算する時間の範囲（開始時刻と終了時刻）
func初期値（初期状態）
t_eval = t解を評価する時刻が格納されたNumPyの配列

4つ目のt_evalだけはpositionalではないので，単なるtではなくt_eval = tとしています*7。solve_ivp関数自体は必ずしも時間等間隔で微分方程式を解く（数値積分）するものではないため，引数としてt_evalを省略すると，結果として得られる後述のsol.tは時間等間隔ではなくなります。もし，解を評価する時刻として所望の時刻があるのであれば（例えば上記のように10 ms毎），t_evalを与える必要があります。ここでは，t = np.arange(0, 10, 0.01)として，時刻t = 0 s ~ 10 sまでを0.01 s (10 ms)間隔で刻むことにしました。要素数は当然ですが1,000個です。

返り値のsolは微分方程式の解を格納する独自のクラス*8となっていて，sol.tで時間を*9，sol.yで解を取り出せます。また，sol.yは2行1000列*10のnumpy.ndarrayであり，それぞれの行がxと\dot{x}に対応しています。ただし，sol.yについては行と列を逆にした方が使い勝手がいいので*11，転置してsol.y.Tとしてデータを取り出します。

早速，Matplotlibを使ってプロットしてみましょう。

fig, ax = plt.subplots()
ax.plot(sol.t, sol.y.T, label = ['$x$', '$\dot{x}$'])
ax.set_xlabel('$t$')
ax.set_ylabel('$x$, $\dot{x}$')
ax.legend()
ax.grid()

これにより，図3のようなプロットを得られます。

図3: 簡単な2階微分方程式\ddot{x} + \dot{x} + 5 x - 4 = 0の初期値x(0) = 0, \dot{x}(0) = 0における解
いかにも2階微分方程式らしい振動波形が見えますね。

車輪の運動方程式をscipy.integrate.solve_ivp関数で解く

微分方程式を表す関数の定義

それでは上の例に沿って(7)式の微分方程式を解いてみましょう*12。車輪の質量Mや半径a，慣性モーメントJなどに具体的な値を代入し，(7)式の微分方程式を表す関数を定義すれば良さそうです。ここではM = 5 kg，a = 0.25 m (25 cm)としてみました。

# Conditions
M = 5                         # Mass, kg
a = 0.25                      # Radius, m
J = M * a**2 / 2              # Inertia, disc

# Input torque calculation
# State y = [x_w, v_w]
def getTorque(t, y):   
    if t < 1:
        tau = 0
    else:
        tau = 0.3
    return tau

# Define wheel ODE
# State y = [x_w, v_w]
def func(t, y):
    # Torque
    _tau = getTorque(t, y)

    dydt = np.zeros_like(y)
    dydt[0] = y[1]            # position is integral of velocity
    dydt[1] = _tau / (M * a + J / a)
    return dydt

8行目でトルクを計算するためのgetTorque関数を定義しています。後述しますが，この関数を使って，トルクの時系列データを求解後に改めて取得します。ここでは，単に時刻t ≥ 1 sの場合に0.3 Nmのトルクを車輪に与えるようにプログラムを組んでいます。

17行目以降が(7)式の微分方程式を表すfunc関数の定義になります。19行目で先のgetTorque関数を呼んでいます。また，22行目以降で(7)式に相当する微分方程式を記述しています。

微分方程式の求解

それでは解いてみましょう。以下のプログラムをご覧ください。

# Solve
dt = 0.001
t = np.arange(0.0, 12.0, dt)
x_w0 = np.array([0, 0])
sol = solve_ivp(func, [0, 12], x_w0, t_eval = t)

# Postprocessing
x_w = sol.y[0,:]
v_w = sol.y[1,:]
theta = ((x_w / a) + np.pi) % (2 * np.pi) - np.pi

# Reproduce torque waveform
tau = np.zeros_like(t)
for i, _t in enumerate(t):
    tau[i] = getTorque(_t, sol.y[:,i])

車輪の初期位置xw = 0 m，初速vw = 0 m/sとして，12秒間の現象についての挙動を求めています。解の評価の時間刻みは1 msです。5行目にてsolve_ivp関数を呼び出して微分方程式を解いています。

8行目以降でsol.yが非常に取り扱いにくいので，位置v_wと速度v_wを個別に取り出しています。また，(3)式に基づいて車輪の角度thetaを車輪の位置x_wから求めています。

13行目以降で，得られた解から再度getTorque関数を呼んで，トルクの時刻歴を格納したtauを再構成しています。これは，solve_ivp関数から呼び出されるfunc関数の中で計算しているトルクを取り出せないためです。特に，この例では単に時刻t ≥ 1 sで一定のトルクを与えているだけですが，例えば状態フィードバック制御のように，func関数内（またはfunc関数から呼び出されるgetTorque関数内）でトルクを動的に計算していた場合，トルクを取り出せないと，後からグラフとしてプロットする際に問題になります。そこで，若干不便ですがこのようなworkaroundを採ることにしました。

解の時間波形をプロット

得られた解をプロットしてみましょう。

# Time-domain plots
fig, ax = plt.subplots(4, 1, figsize = (8, 8))
fig.patch.set_facecolor('lavender')
fig.suptitle(f'Wheel rolling on a floor driven by a torque: $M = {M}$ kg, $a = {a * 100:.2f}$ cm')

# Plot position
ax[0].plot(t, x_w)
ax[0].set_xlabel('Time [s]')
ax[0].set_ylabel('Position, $x_{w}$ [m]')
ax[0].grid()

# Plot speed
ax[1].plot(t, v_w)
ax[1].set_xlabel('Time [s]')
ax[1].set_ylabel('Speed, $v_{w}$ [m/s]')
ax[1].grid()

# Plot angle
ax[2].plot(t, np.degrees(theta))
ax[2].set_xlabel('Time [s]')
ax[2].set_ylabel('Angle of wheel, $\\theta$ [deg]')
ax[2].set_yticks(range(-180, 240, 60))
ax[2].grid()

# Plot torque
ax[3].plot(t, tau)
ax[3].set_xlabel('Time [s]')
ax[3].set_ylabel('Torque, $\\tau$ [Nm]')
ax[3].grid()

fig.tight_layout()

これによって図4を得ます。

図4: 転がる車輪を表す運動方程式の解（時間波形）

上から位置xw，車輪の重心の速度vw，車輪の角度θ，トルクτです。時刻t = 1 s以降で0.3 Nmのトルクが与えられてxの正方向に転がり始めることが読み取れると思います。そう，「読み取れる」だけです。より分かりやすい可視化はないでしょうか…？ そう！ アニメーションです。

アニメーションを作る

本ブログでもたびたびMatplotlibによるアニメーションを使用しています。例えば前回の図1もそうですね。ただし，これまではほぼ「波形のアニメーション」しか作っていませんでした。ここでは，床面や車輪を分かりやすく描いて，物理的な動きをイメージできるようなアニメーションを作っていきます。追加で下記のようにライブラリ・モジュールをインポートします。

import matplotlib.animation as animation

Matplotlibによるアニメーションを作成するためですね。

舞台を作る

まず，車輪が転がる「舞台」を作りましょう。

# Create "theatre" of animation
fig, ax = plt.subplots(1, 1, figsize = (9, 4))
fig.patch.set_facecolor('lavender')
ax.set_aspect('equal')
fig.suptitle(f'Wheel rolling on a floor driven by a torque: $M = {M}$ kg, $a = {int(a * 100)}$ cm')

# Range of floor shown
floor_begin, floor_end = -6, 6

# Set axes
ax.set_xlim(floor_begin, floor_end)
ax.set_xlabel('x [m]')
ax.set_ylim(-1, 4)
ax.set_ylabel('y [m]')
ax.grid()

# Draw floor
ax.plot([floor_begin, floor_end], [0, 0], lw = 2, color = 'black')

# Draw motion equation
ax.text(floor_begin + 0.1, 3.7, r'$\dot{x}_{w} = v$')
ax.text(floor_begin + 0.1, 3.4, r'$\dot{v}_{w} = \tau / (M a + J / a)$')
ax.text(floor_begin + 0.1, 3.1, r'$a \omega = v_{w}$ (no slip)')
ax.text(floor_begin + 0.1, 2.7, r'$J = M a^2 / 2$ (Wheel is a disc.)')
text_time = ax.text(floor_begin + 0.1, 2.4, f'$t = {t[0]:.2f}$ s')

# Draw wheel
wheel = patches.Circle(xy = (x_w[0], a), radius = a, lw = 1.5, ec = 'blue', fc = 'lightblue')
ax.add_patch(wheel)

# Draw wheel angle marker
[line_angle] = ax.plot([x_w[0], x_w[0] - a * np.sin(theta[0])], [a, a + a * np.cos(theta[0])], lw = 1.5, c = 'red')

fig.tight_layout()

18行目でplot関数を応用して「床」を描いています。21 ~ 24行目でtext関数を使って説明書きを加えています。25行目が1つ目のポイントで，text関数を使って時刻を表示しています。ただし，結果として得られるアーティスト（Matplotlibでの図形の呼び方）を変数text_timeに格納しています（表示もされます）。このtext_timeを利用して表示される時刻を更新していきますが，これについては後述します。

28，29行目でpatches.Circle関数を使って半径aの円を描いています。これが「車輪」です。 同じく車輪を表すアーティストをwheelという変数に格納しています。また，32行目でやはりplot関数を使って，車輪の中心から車輪の外周まで赤い線を描いています。これは角度θを表しています。やはりアーティストをline_angleという変数に格納しますが，plot関数はリストを返すためline_angleを大括弧で括って*13リストの中身だけを取り出すようにしています。

車輪を動かす

舞台は完成しました。アニメーションさせてみましょう。アニメーションの作成にはMatplotlibのFuncAnimationという機能を使います。まずは，アニメーションの各フレームを生成するための関数を用意します。下記のupdate関数は後述のmatplotlib.animation.FuncAnimation関数から呼ばれ，引数のiはフレーム番号を表しています。

# Function to update frame
def update(i):
    # Update wheel position
    wheel.center = (x_w[i], a)
    
    # Update wheel angle marker
    line_angle.set_data([x_w[i], x_w[i] + a * np.sin(theta[i])], [a, a + a * np.cos(theta[i])])
    
    # Update time text
    text_time.set_text(f'$t = {t[i]:.2f}$ s')

    return (wheel, line_angle, text_time)

4行目で車輪を表すアーティストを格納したwheelのcenter属性を変更することで車輪の新しい中心位置を設定しています。同じく7行目で角度θを表す赤い線に対してset_dataメソッドを適用して新しい開始位置，終了位置を設定しています（plotなので2点のデータとして与えます）。また，10行目で時刻を表すテキストであるtext_timeに対してset_textメソッドを適用して，表示する時刻を更新します。

12行目で変更を加えた3つのアーティストを格納する変数をタプルにして返します（これにより後述のblit = Trueが活きるようです）。

実際にアニメーションを生成するにはあと2段階の操作が必要です。

# Create animation
ani = animation.FuncAnimation(fig, update, \
    frames = np.arange(0, len(t), 20), interval = (t[1] - t[0]) * 20 * 1000, blit = True)

FuncAnimation関数を呼び，アニメーションを生成します。ここでは引数framesとして解の配列の長さを1/20に間引きしたものを設定しました。引数intervalはアニメーションの1フレームの時間であり，ここではリアルタイム（シミュレーション内での1秒がアニメーションの表示でも1秒）となるように設定しています。blit = Trueとすることで，更新があった部分のみ描き直すように設定します。

FuncAnimation関数の返り値であるaniは，筆者の理解では「こういうアニメーションを作りますという宣言」でしかないため，アニメーションを生成するためにはさらにもう1段階の操作が必要です。例えばアニメーションgifとして保存する場合は，次のように書きます。

ani.save('wheel_animation.gif')

これにより，カレントディレクトリにwheel_animation.gifというアニメーションgifファイルが出来上がります。ここに至って初めてupdate関数を繰り返し呼んでいるようなので，それなりに時間を要します（筆者の環境*14では数分間でした）。

図5: 転がる車輪のアニメーション

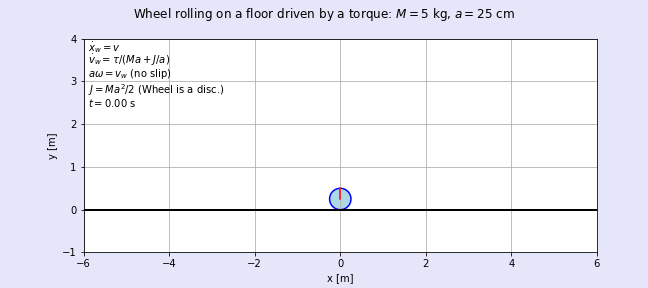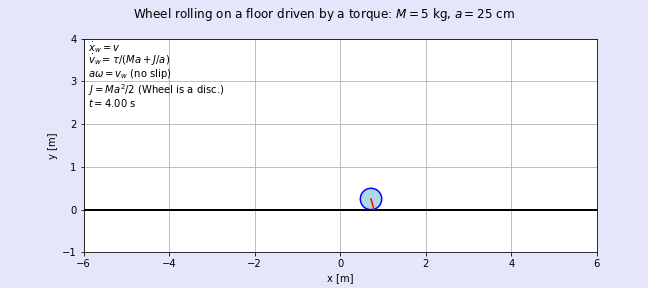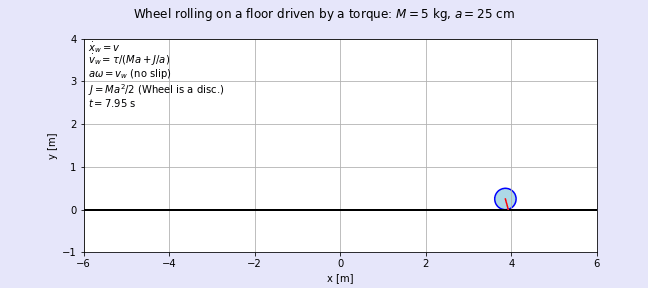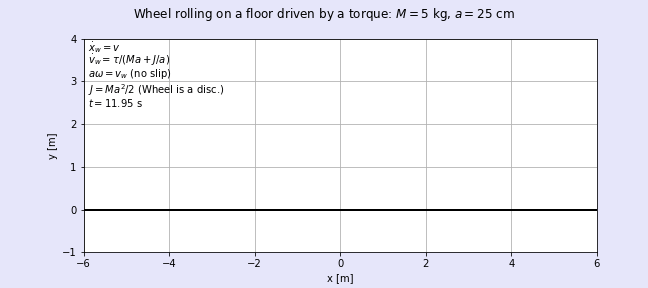
図5に出来上がったアニメーションgifファイルを貼り付けます。図4の波形よりも車輪の動きをイメージし易いのではないでしょうか？

また，以下のように IPythonのHTMLモジュールをインポートすると，HTML5の動画(mp4)としてアニメーションを生成することができます。これは，JupyterLabの中で動画として動く（しかもアニメーションgifより滑らか）ので，本記事のようなアニメーションによる可視化にはうってつけではないかと筆者は思っています（ただし，FFmpegをインストール済みでpathが通っている必要があります）。

from IPython.display import HTML
HTML(ani.to_html5_video())

状態フィードバックを試してみる ～車輪の位置を制御～

図5は原点から車輪が右方向（xの正方向）に転がるだけでした。これでは面白くないので，車輪の位置xwをフィードバック制御してみましょう。先のgetTorque関数を以下のように改造します。

# Control torque calculation
# State y = [x_w, v_w]
def getTorque(t, y):
    F = np.array([-4, -5])
    if t < 1:
        tau = 0
    elif 1 <= t < 6:
        tau = F[0] * (y[0] + 2) + F[1] * y[1]
    else:
        tau = F[0] * (y[0] - 2) + F[1] * y[1]
    return tau

時刻t < 1ではトルクτ = 0 Nmとしますが，時刻t = 1 ~ 6 sでは車輪の位置がxw = −2となるように，また，時刻t = 6 s以降では車輪の位置がxw = 2となるように，状態フィードバック制御します。

同じくscipy.integrate.solve_ivp関数を使って解いてみると，図5のような時間波形を得られます。

図6: 状態フィードバック制御をした場合の解（時間波形）

フィードバックゲイン（上記getTorque関数の4行目）を最適化している訳ではありませんが，どうやら制御できているように見えますね。これをアニメーション化したものが冒頭の図1となります。図1ではアニメーションの「舞台」だけでなく，トルクτ，速度vw，角度θについてもプロットし，その瞬間の時刻を表す赤線をアニメーションとして書き入れてみました。

まとめ

以上でトルクを与えられて回転する車輪について，Python + SciPyを用いて運動方程式を解き，Matplotlibを用いて得られた解をアニメーションにする過程について述べました。これは，車輪形倒立振子のモデル化のための練習でしたが，微分方程式（運動方程式）を表現する関数の書き方や，Matplotlibのアニメーションの生成方法（本ブログの過去の記事で使ったアニメーションとは作り方が異なり，更新されたアーティストのみを書き換えるようにしています）について，いろいろと収穫がありました。

やはり，アニメーションとして動いていると「物理現象をシミュレーションした」という感じがしますね（電気現象ではほとんど時刻歴のプロットしかないので…）。

次回は台車形倒立振子のシミュレーションとアニメーションを取り扱う予定です。本記事ではSciPyを用いましたが，Python Control System Library（やはりSciPyに依存しています）でも非線形なモデルを取り扱うことができるようなので，今後，極配置法や最適レギュレータ，また，オブザーバを用いた現代制御理論の練習をしていくにあたって，SciPyで直接微分方程式を取り扱うのではなく，Python Control System Libaryを使っていこうかと考えています。

参考資料

本記事を執筆するにあたり，以下を参考にさせて頂きました。ありがとうございます。

  1. 早川槙一：「初めての自立移動ロボット制御シミュレーション」，トランジスタ技術，2020年7月号，pp. 71-86
  2. 益川敏英（監修）・植松恒夫・青山秀明（編集）・篠本滋・坂口英継（著）：「基幹講座 物理学 力学」，東京図書，2013年
  3. 倒立振子への道⑧タイヤの運動方程式[129]#つぶやき制御工学 - YouTube

3のこうへいさんのYouTube動画は，y軸方向の動きまで考慮した車輪のモデルになっており，筆者の頭脳では理解が今のところ追いついていません…💧 坂道や段差まで走破する倒立振子を考える場合，このようなモデル化が必要になりますね…。

*1:およびNumPy, SciPy, Matplotlib, JupyterLab

*2:もちろんMATLAB/SimulinkやScilabなど，他にも選択肢はあります。MATLAB Homeはとても心惹かれるものがありますね…。

*3:力fの大きさは，並進運動と回転運動の拘束条件によって決まります。この感覚が筆者には難しかったです。

*4:読者の皆さまにとっては「何を今さら…」というご感想をお持ちのことと拝察します…💧

*5:従来は同様の目的のためにscipy.integrate.odeint関数がありましたが，SciPyの公式ドキュメントでは新規コードへのodeint関数の使用は非推奨となっており，代わりにsolve_ivp関数の使用が推奨されています scipy.integrate.odeint — SciPy v1.10.1 Manual。

*6:solve_ivp関数はもちろん非線形常微分方程式にも適用できます。本ブログでは今後，台車形および車輪形倒立振子のモデリングに挑戦いていきますが，これらは非線形な運動方程式に支配されるシステムです。

*7:その手前でmethod = 'RK45'が省略されています。

*8:scipy.integrate._ivp.ivp.OdeResult型

*9:この条件でのsol.tにはt_evalとして与えたtと同じものが入っています

*10:どうしてこうなった！

*11:ホントにどうしてこうなった！

*12:考えてみたら上記の例よりも車輪の運動方程式の方が単純でした…💧

*13:「line_angle,」のようにタプルとして受けるやり方もあるようです。そちらが正しい？

*14:Sandy Bridge...!!