The Negligible Lab

Astray in the forest of electrical and electronic circuits. Adrift in the gap between time and frequency domains. 独立独歩を是とする。

Pythonによる車輪形倒立振子の運動方程式の導出

制御工学 Python SymPy SciPy Matplotlib JupyterLab

はじめに

P計画

前々回，前回にて台車形倒立振子の運動方程式を導出し，シミュレーション，アニメーション，線形化，最適レギュレータの作り方について書き散らして参りました。本記事以後，いよいよ台車形から車輪形の倒立振子に歩みを進め，運動方程式の導出，シミュレーション，アニメーションについて書いていきます。ただし本記事では紙面（？）の都合上，SymPyにおいて力学系をシステマティックに取り扱うsympy.physics.mechanicsというモジュールを用いた運動方程式の導出に焦点を当て，シミュレーションとアニメーションは次回に譲りたいと思います。

まだまだシミュレーションでしかありませんが，ここで制御設計についての理解を深めてから実機の設計・製作，ソフトウェア実装を進め，願わくば年末頃には実際の車輪形倒立振子を立てることができればと夢想しております。

完成したアニメーション

運動方程式を導出したらそれをSciPyで解き，Matplotlibにてアニメーションにします。図1に完成した車輪形倒立振子のアニメーションを示します。車輪の質量M = 0.2 kg，車輪の半径a = 0.1 m，振り子の質量m = 1.5 kg，振り子の長さ2l = 0.6 mであり，車輪の初期位置xw0 = 1 m，振り子の初期角度θ0 = 15°の動きを可視化しています。ここではトライ・アンド・エラーで求めた状態フィードバックゲインを用いて倒立させており，時刻t = 5 sから0.5秒間のステップ状の外乱，時刻t = 8 sからの正弦波状の外乱にも負けずに倒立を維持している様子が見えますね。時刻t = 15 s以降は制御を止めます。当たり前ですが振り子の倒立が維持できなくなり，逆さまになってぶらぶらと振動します。

図1: 車輪形倒立振子のアニメーション

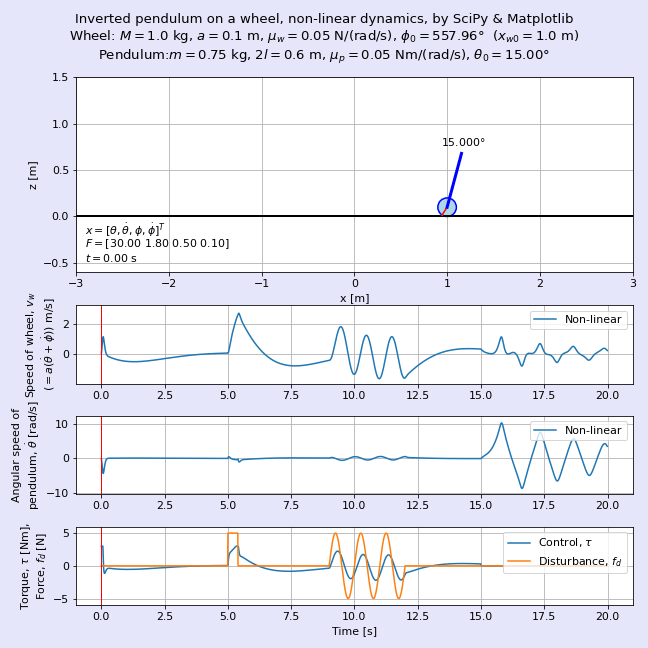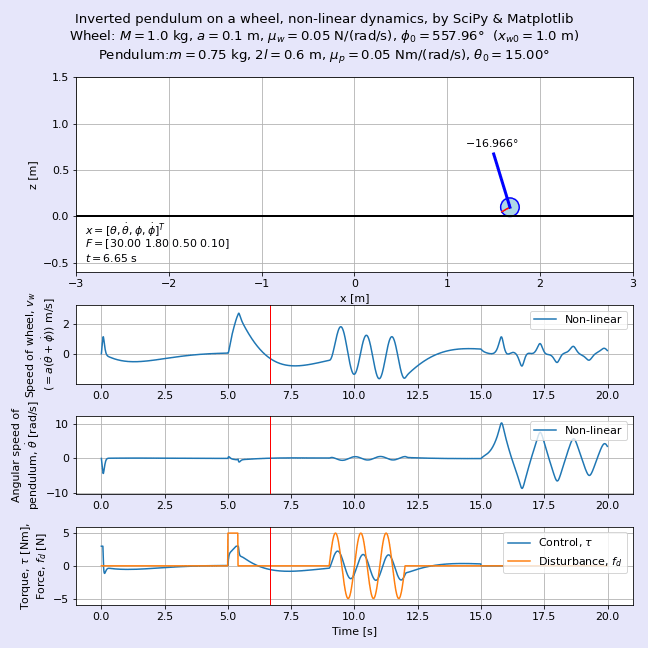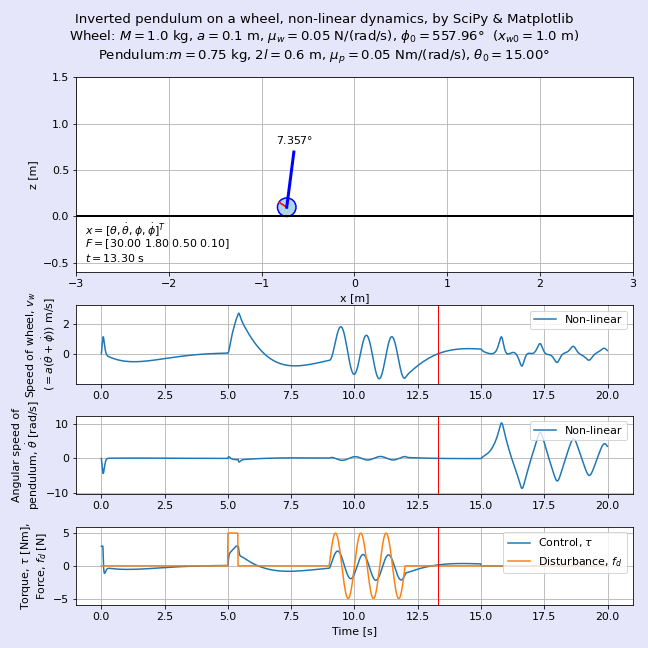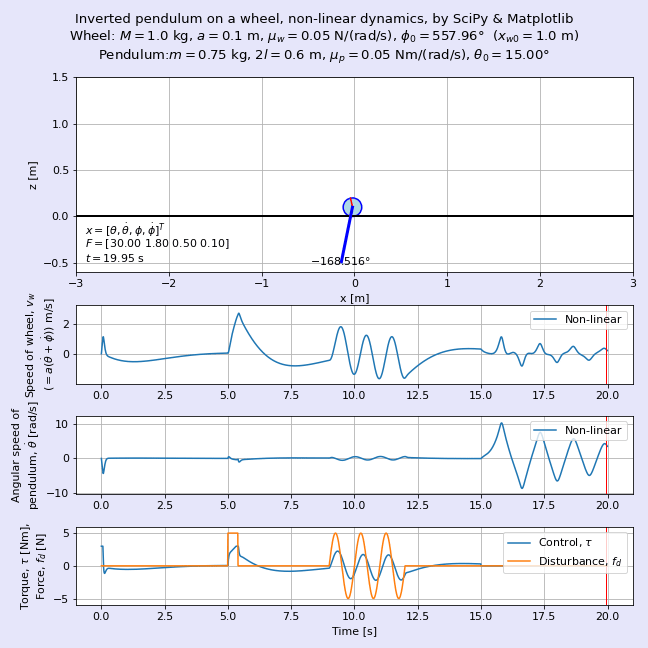
力学的な観点からみると，車輪も振り子も剛体なので，一見して運動方程式は台車形*1より複雑になりそうです。本記事では数式処理ライブラリSymPyのsympy.physics.mechanicsモジュールを用いてシステマティックに運動方程式を導出することを試みます。

目次

SymPyによる力学系の取り扱いとその例

sympy.physics.mechanicsモジュール

前々回では台車形倒立振子の運動方程式を力のつり合いの関係から言わば「手動で」導出していました。しかしその過程で，Pythonの数式処理ライブラリSymPyに力学系を取り扱う仕組みが存在することを知りました。正式には“sympy.physics.mechanics”という名前のモジュールですが，長いので本記事では“SymPy Mechanics”と呼ぶことにします（必要に応じて元の名前でも呼びます）。

docs.sympy.org

SymPy Mechanicsでは質点や剛体をオブジェクトとして定義し，その位置や速度，拘束条件，ポテンシャルエネルギーなどを与えてあげれば，オイラー・ラグランジュ方程式から運動方程式を導出できるというのです。これなら複雑な系でもある程度簡単に運動方程式を導けるはず…。台車形倒立振子の際には台車を質点として扱いましたが，車輪形倒立振子では車輪も振り子もともに剛体となるので，少しですがより複雑になるはずです。数学弱者である筆者の手計算という信用すべからざるものに頼るのではなく，SymPy Mechanicsで体系的に運動方程式を導出するのが筋ではないかと考えました。

簡単な例: 質点の自由落下

質点が空気抵抗を受けながら自由落下する場合を例にSymPy Mechanicsでの運動方程式導出を試みます*2。

図2: 質点の自由落下（重力と空気抵抗）

図2に，質量mの質点Pが重力mgを受けて自由落下している場合の概略図を示します。質点Pは速度に比例した空気抵抗を受けるものとします。また，鉛直下向きにx軸を取り，Pのx座標をxpとします。この例はごく簡単ですので，運動方程式としては次式のように書けることはほぼ説明不要と言えるでしょう。

m \ddot{x}_p = m g - \mu \dot{x}_p \tag{1}

この例はごく簡単です。これより少し複雑な系でも手計算で行けるでしょう。しかし，もっと複雑な例におけるSymPy Mechanicsの使い方を概観するため，あえてこの簡単な例についてSymPy Mechanicsの仕組みを適用し，オイラー・ラグランジュ方程式から(1)式を導出してみます。まず，必要なライブラリ・モジュールをインポートしておきましょう。

import sympy as sp
from sympy.physics.mechanics import *
init_vprinting()

これまでの記事でも述べた通り，init_vprinting関数を実行しておくと，dynamicsymbols（時刻tの関数）として定義された変数の時間微分をドットを用いるニュートン記法で表示してくれます。

座標系，点，質点の定義

SymPy Mechnics (sympy.physics.mechnics)で力学系の問題を解く場合，運動の舞台となる座標系，つまりReferenceFrameオブジェクトを作成します。

# Define reference frame
N = ReferenceFrame('N')

ここではこのようにNという名前の座標系を作りました。この例ではこの1つで十分です*3。

次に，落下している質点を作りましょう。質点を定義する場合，PointオブジェクトとParticleオブジェクトをセットで作成します。これが若干分かり難いのですが，Pointオブジェクトは位置と速度の情報を保持しているものの，質量の情報をもっていません。一方，Particleオブジェクトは位置と速度を表すためにPointオブジェクトをプロパティとしてもっており，かつ，質量の情報を保持しています。実際，やってみましょう。ここでは必要な変数（シンボル）も一緒に定義します。

# Define symbols
m, g = sp.symbols('m g')        # Mass and gravity
mu = sp.symbols('mu')           # Air resistance
t = sp.symbols('t')             # Time

# Define dynamic symbols
x_p = dynamicsymbols('x_p')     # Position of particle

# Define point and particle
po = Point('po')
pa = Particle('pa', po, m)

SymPyの公式ドキュメントにある例のやり方に沿って，10，11行目にあるように，Pointオブジェクトをpo，Particleオブジェクトをpaと名付けて定義しました。一文字だと両方とも“P”になってしまうので，poとpaとするのは苦肉の策ですね。ここではPointオブジェクトpoの位置や速度はまだ設定していません。また，ParticleオブジェクトpaはPointオブジェクトpoと質量mをプロパティとしてもっています。

速度と位置エネルギー

次に，質点Pの速度と位置（ポテンシャル）エネルギーを設定します。

# Set velocity and potential energy of particle
po.set_vel(N, x_p.diff(t, 1) * N.x)
pa.potential_energy = -m * g * x_p

Pointオブジェクトpoのset_velメソッドで速度を設定しますが，ここでは最初に定義した座標系Nのx方向の単位ベクトルN.xを使ってx_p.diff(t, 1) * N.xと定義します。要するに質点Pの速度は\dot{x}_{p}であると当たり前のことを宣言しているだけです。ちなみに，poに速度を設定し，paに質量を設定すると，paのもつ運動エネルギーが自動的に計算されます。

また，位置エネルギーをParticleオブジェクトpaのpotential_energy属性に代入する形で設定しています。x軸を下に向けたので-m * g * x_pですね*4。

さて，筆者としてはつまづきポイントだと思うのですが，位置や速度はPointオブジェクトpoが持っており，位置エネルギー（と運動エネルギー）はParticleオブジェクトpaが持っているということです。これは筆者の推測ですが，Pointオブジェクトは「運動学(kinematics)」を記述するために存在するからではないかと考えます。例えば，「基幹講座物理学 力学」（東京図書，2013年）の第1章の冒頭には以下のような記述があります。

物体が動く様子を記述する一般的枠組みを「運動学(kinematics)」とよぶ．運動学では物体の運動の原因を問うのではなく，運動の幾何学的記述に専念する．（中略）ここでは力(force)という概念には立ち入らず…（後略）

したがって，質量とか力といった概念と切り離して「運動」，すなわち位置，速度，加速度だけを記述するというのがSymPy MechanicsでのPointオブジェクトの役割で，質量や力，運動量，エネルギーはParticleオブジェクトに持たせるという方式になっているのではないかと筆者個人としては考えています。

一般化座標と一般化力の定義

これはわざわざ定義しなくても良いのですが，オイラー・ラグランジュ方程式を使っている感を醸し出すために，以下のようにqとfを定義してみました。

# Define generalized coordinates
q = [x_p]

# Define generalized force, air resistance
f = [(po, -mu * x_p.diff(t, 1) * N.x)]

一般化座標qはただx_pですが，1つだけの要素をもつリストとしています。一般化力fについては，要素としてタプルを1つだけもつリストとして定義しており，そのタプル(po, -mu * x_p.diff(t, 1) * N.x)はPointオブジェクトpoに対して大きさ\mu \dot{x}_{p}の力が座標系Nのx軸の負方向に働く（すなわち空気抵抗）ということを表しています。

今のところの筆者の理解では，SymPy Mechanicsには散逸関数Dを扱う仕組みがないように見えます。散逸関数Dがあれば，空気抵抗fについて

D = \displaystyle \frac{1}{2} \mu \dot{q}^{2},\quad f = \displaystyle \frac{\partial D}{\partial \dot{q}} \tag{2}

と書いて，後述するLagrangesMethodにDとして渡せると思われるのですが，それができないようなのでfとして渡しています。

ラグランジアンと運動方程式の導出

手動での導出

ここではまず「手動」でラグランジアンと運動方程式を導出しておきましょう。ラグランジアンLは運動エネルギーTとポテンシャル（位置）エネルギーUの差です。

L = T - U = \displaystyle \frac{1}{2} m \dot{q}^{2} - (- m g q) = \displaystyle \frac{1}{2} m \dot{q}^{2} + m g q \tag{3}

一次元の運動しか扱っていないので，もちろんここではq = x_{p}です。得られたラグランジアンLをオイラー・ラグランジュ方程式

\displaystyle \frac{d}{dt} \frac{\partial L}{\partial \dot{q}} - \frac{\partial L}{\partial q} = f \tag{4}

に代入してみると，

\displaystyle \frac{d}{dt} (m \dot{q}) - mg = f \tag{5}

となりますが，f = -\mu \dot{q}とq = x_{p}を代入して整理すれば，

m \ddot{x}_p = m g - \mu \dot{x}_p \tag{6}

を得ます。これは(1)式と全く同じ式です。

SymPy Mechanicsの仕組みを使う

次に，手動ではなく，SymPy Mechanicsの仕組みを使って導出してみます。PointオブジェクトpoとParticleオブジェクトpaを通じて質点Pの速度，質量，位置エネルギーを既に設定しているので，ラグランジアンはLagrangian関数で自動的に計算可能です。

L = Lagrangian(N, pa)

座標系NにおけるParticleオブジェクトpaのラグランジアンを変数Lに代入します。さらに，LagrangesMethodオブジェクト*5を定義し，変数LMに格納します。

LM = LagrangesMethod(L, q, forcelist = f, frame = N)

LagrangesMethodの定義（初期化）にあたっては，ラグランジアンL，一般化座標q，forcelistとして一般化力f，frameとして座標系Nを与えます。最後に，運動方程式を導出します。

eom = LM.form_lagranges_equations()
display(eom)

LMのform_lagranges_equationsメソッドを呼び出すと，ラグランジアンがオイラー・ラグランジュ方程式に代入されて運動方程式が導かれます。結果を変数eomに代入しました。JupyterLabで使えるdisplay関数でeomを表示すると，

\displaystyle [- g m + m \ddot{x}_{p} + \mu \dot{x}_{p} ] \tag{7}

と表示されます。これはSymPyでの取り扱いの特徴ですが，方程式において「= 0」の部分を省略した書き方になっており，かつ，多次元である場合と同様にリストとして表示されています（このため大括弧に入っています）。(7)式はよく見比べれば，(6)式と（したがって(1)式とも）一致していることが判ります。

以上で，空気抵抗を受けながら自由落下する質点の運動方程式をSymPy Mechanicsで導出することができました。

車輪形倒立振子の運動方程式の導出

いよいよ車輪形倒立振子の運動方程式を導出してみます。以上で述べた例との相違点は，車輪も振り子も質点ではなく剛体であるという点です。剛体については後述のようにRigidBodyオブジェクトで表現します。

考える系

図3に今回考える車輪形倒立振子の概略図を示します。

図3: 車輪形倒立振子の全体図

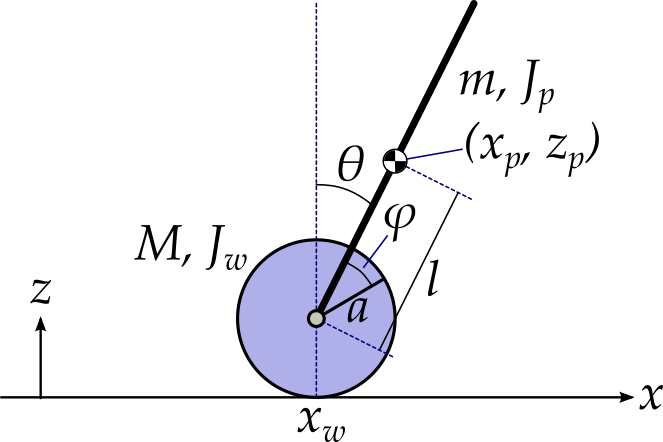
水平方向をx軸，鉛直方向をz軸とし，紙面（画面？）に垂直な方向をy軸とします。車輪形倒立振子の基本構造は，車輪の中心にピボットがあり，振り子の一端が取り付けられたものです。振り子にモータ等のトルク源を取り付け，車輪と振り子にトルクを加えることによって車輪の回転と振り子の倒立維持を図ります。

車輪の質量をM，半径をa，慣性モーメントをJw，車輪のx座標をxwとし，振り子の質量をm，長さを2l，重心の周りの慣性モーメントをJpとし，重心の座標を(xp, zp)とします。また，鉛直方向と振り子がなす角度をθ，振り子と車輪の基準動径のなす角をφとします。

この系の運動方程式をSymPy Mechanicsで導出していきます。なお，車輪形運動方程式の導出に関しては，おかしょさんのブログ「そらたまご」の記事を（大いに）参考にさせて頂いております。

okasho-engineer.com

この場を借りて謹んで御礼申し上げます。

車輪と振り子を表す剛体（RigidBodyオブジェクト）

まずは，車輪と振り子に分けて，剛体や座標系の定義を考えていきます。図4に車輪と振り子に分けた車輪形倒立振子を示します。

図4: 車輪と振り子に分けた車輪形倒立振子

SymPy Mechanicsでは剛体（RigidBodyオブジェクト）を生成する際に，質点（Particleオブジェクト）に必要だったPointオブジェクトと質量に加えて，慣性モーメントと座標系を必要とします。Pointオブジェクトは重心を表します。また，剛体はその座標系に貼り付いているとして取り扱われます。言わば，この座標系は剛体の回転角度を管理するための存在です。質点を表すParticleオブジェクトにおいて，位置と速度はPointオブジェクトによって保持されていましたが，これと同様に，剛体においてはその回転角度は座標系によって保持されます。これもなかなか分かり難いポイントです。ここでは，図4にも示す通り，全体の座標系をN，振り子の座標系をA，車輪の座標系をBすることにします。

車輪と振り子を回転させる制御トルクをτ (= tau)とし，車輪と振り子に働く角速度に比例した摩擦トルクをそれぞれτfw，τfpとします。

それでは，シンボル，座標系，剛体を定義していきましょう。まずは全体に共通するものから始めます。

# ------------------------------------------------
# Common symbols and reference frame
# ------------------------------------------------

# Define symbols, Common
t = sp.symbols('t')                                    # Time
g = sp.symbols('g')                                    # Gravity

# Define reference frame, Common
N = ReferenceFrame('N')
O = Point('O')                                         # Origin point
O.set_vel(N, 0)

時刻t，重力加速度gを定義した後，全体の座標系Nを定義し，さらにPointオブジェクトとしてO点を定義します。O点の速度としてset_velメソッドで零を設定します。固定されている点，原点の代わりと言っても良いでしょう。

いよいよ剛体を定義します。最初に振り子に相当する剛体（RigidBodyオブジェクト）です（参考にしたおかしょさんの「そらたまご」の記事をはじめ，振り子の角度を基準に車輪の角度を与えている例が多いので，車輪より先に振り子を定義します）。

# ------------------------------------------------
# Pendulum
# ------------------------------------------------

# Symbols
m, J_p, l, mu_p = sp.symbols('m J_p l mu_p')           # Mass, Inertia, length, and friction
theta = dynamicsymbols('theta')                        # Angle with respect to vertical line

# Reference frame and rigid body
A = N.orientnew('A', 'Axis', (theta, N.y))             # Define new reference frame for pendulum
A.set_ang_vel(N, theta.diff(t, 1) * N.y)               # Set angular velocity of reference frame
C_p = Point('C_p')                                     # Mass center of pendulum
J_p_tensor = J_p * outer(A.y, A.y)                     # Inertia tensor
P = RigidBody('P', C_p, A, m, (J_p_tensor, C_p))       # Definition of rigid body

質量，慣性モーメント（の大きさ），長さ，抵抗係数（速度に比例した摩擦力の係数）のシンボルm，J_p，l，mu_pをそれぞれ定義します。また，時刻tの関数であるdynamicsymbolsとしてtheta (= θ)を定義します。これは後述する一般化座標の成分となります。

10行目で座標系Nにorientnewメソッドを適用してy軸の周りに角度theta (= θ)だけ回転した新しい座標系を生成し，変数Aに代入します。座標系Aですね。さらに，座標系Aの座標系Nに対する角速度をtheta.diff(t, 1) * N.y (= \dot{\theta})として定義します。ここで，角速度はy軸回りの回転であることを明確にするため，座標系Nのy軸方向の単位ベクトルN.yを掛けてベクトルにしています。

次に重心C_pを定義し，慣性モーメントとしてy軸回りの慣性モーメントを表すテンソルを表現するため，J_p_tensor = J_p * outer(A.y, A.y)と書いています*6。

最後の行で振り子を表す剛体Pを定義しています。“P”という名前，重心C_p，座標系A，質量mを設定し，さらに慣性モーメントテンソルJ_p_tensorと回転軸であるC_pを与え，オブジェクトとしてPを生成します。

次に車輪に相当する剛体（RigidBodyオブジェクト）を定義します。

# ------------------------------------------------
# Wheel
# ------------------------------------------------

# Symbols
M, J_w, a, mu_w = sp.symbols('M J_w a mu_w')
phi = dynamicsymbols('phi')

# Reference frame and rigid body
B = A.orientnew('B', 'Axis', (phi, A.y))               # Define new reference frame for wheel
B.set_ang_vel(A, phi.diff(t, 1) * A.y)                 # Set angular velocity of reference frame
C_w = Point('C_w')                                     # Center of wheel
J_w_tensor = J_w * outer(B.y, B.y)                     # Intertia tensor
W = RigidBody('W', C_w, B, M, (J_w_tensor, C_w))       # Definition of rigid body

質量，慣性モーメント（の大きさ），半径，抵抗係数（速度に比例した摩擦力の係数）のシンボルM，J_w，a，mu_wをそれぞれ定義します。また，時刻tの関数であるdynamicsymbolsとしてphi (= φ)を定義します。これは後述する一般化座標の成分となります。

10行目で座標系Aにorientnewメソッドを適用してy軸の周りに角度phi (= φ)だけ回転した新しい座標系を生成し，変数Bに代入します。座標系Bですね。さらに，座標系Bの座標系Aに対する角速度をphi.diff(t, 1) * N.y (= \dot{\phi})として定義します。ここで，角速度はy軸回りの回転であることを明確にするため，座標系Aのy軸方向の単位ベクトルA.yを掛けてベクトルにしています。

次に重心C_wを定義し（車輪なので重心イコール中心です），慣性モーメントとしてy軸回りの慣性モーメントを表すテンソルを表現するため，J_w_tensor = J_w * outer(B.y, B.y)と書いています*7。

最後の行で車輪を表す剛体Wを定義しています。“W”という名前，重心（= 中心）C_w，座標系B，質量Mを設定し，さらに慣性モーメントテンソルJ_w_tensorと回転軸である重心C_wを与え，オブジェクトとしてWを生成します。

拘束条件

本記事で検討する倒立振子では，車輪が地面から離れないと仮定します。もちろん，車輪と地面の間のバウンドなども考えれば，坂道や荒れ地を走行する倒立振子ロボットなどもモデル化できるはずですが，筆者のスキル不足ゆえに簡単のため，車輪は地面から離れないと考えることにします。この場合，車輪の中心の座標(xw, zw)は，

\begin{align} x_{w} &= a (\theta + \phi) \\[5pt] z_{w} &= a \end{align} \tag{8}

と書くことができ，これを時刻tで微分すれば速度として，

\begin{align} \dot{x}_{w} &= a (\dot{\theta} + \dot{\phi}) \\[5pt] \dot{z}_{w} &= 0 \end{align} \tag{9}

を得ます。

また，車輪の中心と振り子の端点が離れてバラバラになることはありませんので，車輪の中心と振り子の重心の間に拘束条件が存在します。座標系Nにおける振り子の重心の座標(xp, zp)は，

\begin{align} x_{p} &= x_{w} + l \sin \theta = a (\theta + \phi) + l \sin \theta \\[5pt] z_{p} &= a + l \cos \theta \end{align} \tag{10}

と書くことができます。また，これを時刻tで微分すれば速度を得ることができて，

\begin{align} \dot{x}_{p} &= \dot{x}_{w} + l \dot{\theta} \cos \theta = a (\dot{\theta} + \dot{\phi}) + l \dot{\theta} \cos \theta \\[5pt] \dot{z}_{p} &= -l \dot{\theta} \sin \theta \end{align} \tag{11}

となります。

これらの拘束条件をSymPy Mechanicsにおいても設定します。車輪の中心を表すPointオブジェクトC_wと振り子の重心を表すPointオブジェクトC_pの位置と速度を，set_posメソッドとset_velメソッドでそれぞれ設定します。

# ------------------------------------------------
# Constraints
# ------------------------------------------------

# Set positions
C_w.set_pos(O, a * ((theta + phi) * N.x + N.z))
C_p.set_pos(C_w, l * (sp.sin(theta) * N.x + sp.cos(theta) * N.z))

# Set velocities
C_w.set_vel(N, a * (theta.diff(t, 1) + phi.diff(t, 1)) * N.x)
C_p.set_vel(N, (a * (theta.diff(t, 1) + phi.diff(t, 1)) 
   + l * theta.diff(t, 1) * sp.cos(theta)) * N.x \
   - l * theta.diff(t, 1) * sp.sin(theta) * N.z)

(8) ~ (11)式の内容をほとんどそのまま設定していることが判ると思います。ただし，車輪の重心C_wについては基準点Oからの相対位置，また，振り子の重心C_pについては車輪の中心C_wからの相対位置で設定しています。

次に，（必ずしも「拘束条件」を構成している訳ではありませんが）外乱を加えるポイントを定義します。外乱は振り子の先端に水平方向（座標系Nにおけるx方向）に加えるものとします。

# Point to apply disturbance
P_d = Point('P_d')
P_d.set_pos(C_p, l * A.z)
P_d.set_vel(N, (a * (theta.diff(t, 1) + phi.diff(t, 1)) \
    + 2 * l * theta.diff(t, 1) * sp.cos(theta)) * N.x \
    - 2 * l * theta.diff(t, 1) * sp.sin(theta) * N.z)

PointオブジェクトとしてP_dを定義し，set_posメソッドとset_velメソッドを用いて，位置と速度を振り子の先端でのそれらに設定します。

運動エネルギーと位置エネルギー

2つの剛体について重心の速度と回転角速度を設定しましたので，運動エネルギーを書くことができます。以下のようにJupyterLabに打ち込んで確認してみましょう。

# ------------------------------------------------
# Kinetic energies
# ------------------------------------------------
print('Kinetic energy, Pendulum:')
display(P.kinetic_energy(N))

print('Kinetic energy, Wheel:')
display(W.kinetic_energy(N))

すると，振り子の運動エネルギーTpと車輪の運動エネルギーTwについて，次式のように表示されるはずです（並進の運動エネルギーと回転の運動エネルギーの和ですね）。

T_{p} = \displaystyle \frac{J_{p} \dot{\theta}^{2}}{2} + \frac{m\left(l^{2} \sin^{2}{\left(\theta \right)} \dot{\theta}^{2} + \left(a \left(\dot{\phi} + \dot{\theta}\right) + l \cos{\left(\theta \right)} \dot{\theta}\right)^{2}\right)}{2} \tag{12}
T_{w} = \displaystyle \frac{J_{w} \left(\dot{\phi} + \dot{\theta}\right) \dot{\phi}}{2} + \frac{J_{w} \left(\dot{\phi} + \dot{\theta}\right) \dot{\theta}}{2} + \frac{M a^{2} \left(\dot{\phi} + \dot{\theta}\right)^{2}}{2} \tag{13}

なお，(12)，(13)式の右辺はJupyterLab上での表示からそのまま\mathrm{\LaTeX}形式の表現をコピー & ペーストしました。

次に，位置エネルギーを設定します。車輪は地面から離れないので位置エネルギーを持つのは振り子のみです。振り子のもつ位置エネルギーUpは

U_{p} = m g z_{p} = m g l \cos \theta \tag{14}

と書けます*8。これをRigidBodyオブジェクトPのもつ位置エネルギーとして設定します。Pのpotential_energy属性にそのまま代入するだけですね*9。

# ------------------------------------------------
# Potential energies
# ------------------------------------------------
P.potential_energy = m * g * l * sp.cos(theta)
print('Potential energy of pendulum:')
display(P.potential_energy)

以上で剛体の持つ運動エネルギーと位置エネルギーを設定できましたので，ラグランジアンを計算できるはずです。

ラグランジアンと運動方程式の導出

ラグランジアン

ラグランジアンは次式で表すことができます。

L = T_{p} + T_{w} - U_{p} \tag{15}

しかしこれを直接入力する必要はありません。

# ------------------------------------------------
# Euler-Lagrange method
# ------------------------------------------------

# Get Lagrangian
L = Lagrangian(N, P, W)
print('Lagrangian:')
display(L)

このように，Lagrangian関数に（最終的に運動方程式を表現したい）座標系N，RigidBodyオブジェクトPとWを与えてあげれば自動的に計算できます。ここでは変数Lに結果を格納します。一応書き出してみると，

\begin{align} L &= \displaystyle \frac{J_{p} \dot{\theta}^{2}}{2} + \frac{J_{w} \left(\dot{\phi} + \dot{\theta}\right) \dot{\phi}}{2} + \frac{J_{w} \left(\dot{\phi} + \dot{\theta}\right) \dot{\theta}}{2} + \frac{M a^{2} \left(\dot{\phi} + \dot{\theta}\right)^{2}}{2} \\[5pt] &- g l m \cos{\left(\theta \right)} + \frac{m \left(l^{2} \sin^{2}{\left(\theta \right)} \dot{\theta}^{2} + \left(a \left(\dot{\phi} + \dot{\theta}\right) + l \cos{\left(\theta \right)} \dot{\theta}\right)^{2}\right)}{2} \end{align} \tag{16}

です。

一般化座標と一般化力

次に，一般化座標と一般化力を設定しましょう。一般化座標については，

q = [\theta, \phi]^{T} \tag{17}

と振り子と車輪の角度を設定するだけです。

# Generalized coordinate
q = [theta, phi]

一般化力については少し説明が要ると思われます。まず，制御トルクτですが，これは振り子に搭載されているモータなどのトルク源から車輪を回そうとするものですが，作用・反作用の法則から，車輪を回そうとしてトルクを加えれば，反作用で振り子を反対方向に回そうとするトルクが同時に発生するはずです*10。したがって，RigidBodyオブジェクトとしては振り子Pと車輪Wの両方に同じ大きさで逆向きのトルクが発生するように表現する必要があります。そして振り子Pと車輪Wはそれぞれ座標系AとBに貼り付いており，SymPy MechanicsでのトルクはPやWに直接作用させるというよりは，座標系A，Bに作用させるように記述します。具体的には以下のように書きます。

# Generalized forces and torques
# Control torque
tau = sp.symbols('tau')
f_control = [(A, -tau * A.y), (B, tau * B.y)]

f_controlは制御トルクに関する一般化力の成分です。（座標系，その座標系に加えるトルク）という形をしたタプルのリストですね。図3，4において紙面（画面？）を貫くy軸方向が回転軸となるので，トルクには座標系A，Bでのy軸方向の単位ベクトルA.y，B.yをそれぞれ掛けてベクトルにしています。

少し駆け足気味になってまいりましたが，次は摩擦トルクです。摩擦に関しては，以下の2つをきちんと分けて考える必要がありそうです。

  1. 振り子と車輪の間の摩擦トルク: 相対角速度\dot{\phi}に比例係数\mu_{p}を乗じた値になり，作用・反作用の法則から車輪と振り子に対して逆向きに働く。
  2. 車輪と床の間の摩擦トルク（転がり抵抗）: 車輪の角速度\dot{\theta} + \dot{\phi}に比例係数\mu_{w}を乗じた値になり*11，車輪のみに働く（床にも働くが床は動かない）。

RigidBodyオブジェクトとしての振り子Pの座標系であるAに対しては上記1のみ，車輪Wの座標系Bに対しては上記1と2がともに加わることになります。これを表現すれば以下のように書けます。

# Friction or dissipative
# Friction between pendulum and wheel
tau_fp = sp.symbols('tau_fp')
tau_fp = mu_p * phi.diff(t, 1)

# Friction between pendulum and wheel and friction between wheel and floor
tau_fw = sp.symbols('tau_fw')
tau_fw = -mu_p * phi.diff(t, 1) - mu_w * (theta.diff(t, 1) + phi.diff(t, 1))

f_dissipation = [(A, tau_fp * A.y), (B, tau_fw * B.y)]

f_dissipationは摩擦トルク（散逸項）に関する一般化力の成分です。

外乱力です。前々回，前回のように振り子の先端に外乱力fdを水平（すなわち座標系Nでのx方向）に加えることを考えます。外乱を加える点については既にP_dとして定義済みです。一般化力は（点，力）という形をしたタプルのリストですが，具体的には以下のように書けます。外乱力は座標系Nのx方向に加えるのでN.xを掛けてベクトルにしています。

# Disturbance force
f_d = sp.symbols('f_d')
f_disturbance = [(P_d, f_d * N.x)]

最後に，定義した一般化力の成分を足してfという変数に格納します。これは単純にPythonのリストの和なので要素が連結されただけですね。各要素は（座標系，トルク）または（点，力）という形のタプルです。

# Summation of generalized forces and torques
f = f_control + f_dissipation + f_disturbance
いよいよ運動方程式へ

ここまでの準備が整ったら，質点の自由落下の例と同様の手順で運動方程式を導出できます。

# Define a Lagrange's method
LM = LagrangesMethod(L, q, forcelist = f, frame = N)

# Derive equation of motion!
eom = LM.form_lagranges_equations()
print('Equation of motion:')
display(eom[0].simplify().factor())
display(eom[1].simplify().factor())

導出した運動方程式をeomという変数に格納します。一般化座標がq = [θ, φ]Tですので，eomは2つの方程式からなるリストです。複雑ですが，書き出してみると，

\begin{align} \displaystyle J_{p} \ddot{\theta} &+ J_{w} \ddot{\phi} + J_{w} \ddot{\theta} + a^{2} M \ddot{\phi} + a^{2} M \ddot{\theta} + a^{2} m \ddot{\phi} + a^{2} m \ddot{\theta} - a f_{d} \\\ &- a m l \dot{\theta}^{2} \sin \theta + a m l \ddot{\phi} \cos \theta + 2 a m l \ddot{\theta} \cos \theta \\\ &- 2 f_{d} l \cos \theta - m l g \sin \theta + m l^{2} \ddot{\theta} + \mu_{w} \dot{\phi} + \mu_{w} \dot{\theta} = 0 \end{align} \tag{18}
\begin{align} \displaystyle J_{w} \ddot{\phi} &+ J_{w} \ddot{\theta} + a^{2} M \ddot{\phi} + a^{2} M \ddot{\theta} + a^{2} m \ddot{\phi} \\\ &+ a^{2} m \ddot{\theta} - a f_{d} - a m l \dot{\theta}^{2} \sin \theta + a m l \ddot{\theta} \cos \theta \\\ &+ \mu_{p} \dot{\phi} + \mu_{w} \dot{\phi} + \mu_{w} \dot{\theta} - \tau = 0 \end{align} \tag{19}

となります*12。台車形倒立振子に比べるとやはりかなり複雑に見えますね…。おかしょさんの「そらたまご」の記事に準じていくつかの成分を括り出せば，

\begin{align} \{ J_{w} &+ J_{p} + a^{2} (M + m) + m l (l + 2 a \cos \theta) \} \ddot{\theta} \\\ &+ \{J_{w} + a^{2} (M + m) + a m l \cos \theta\} \ddot{\phi} \\\ &- a m l \dot{\theta}^{2} \sin \theta - m g l \sin \theta \\\ &= -\mu_{w} (\dot{\theta} + \dot{\phi}) + (a + 2 l \cos \theta) f_{d} \end{align} \tag{20}
\begin{align} \{ J_{w} & + a^{2} (M + m) + a m l \cos \theta \} \ddot{\theta} \\\ &+ \{J_{w} + a^{2} (M + m)\} \ddot{\phi} - a m l \dot{\theta}^{2} \sin \theta \\\ &= \tau - \mu_{w} (\dot{\theta} + \dot{\phi}) - \mu_{p} \dot{\phi} + a f_{d} \end{align} \tag{21}

と書くこともできます。

非線形状態方程式への布石

前々回の台車形倒立振子の際にも述べましたが，(18) ~ (21)式のままではSciPyのscipy.integrate.solve_ivp関数を用いた求解はできません。非線形状態方程式の形に整理するため，(18) ~ (21)式を角加速度である\ddot{\theta}と\ddot{\phi}の連立方程式とみなして解く必要があります。具体的には以下のように処理します。

# ------------------------------------------------
# Angular acceleration
# ------------------------------------------------

# Solve equation of motion with respect to the second-order variables
sol = sp.solve(eom, [theta.diff(t, 2), phi.diff(t, 2)])

eq1 = sol[theta.diff(t, 2)].simplify()
print('Equation with respect to d^2 theta / dt^2')
display(eq1)

eq2 = sol[phi.diff(t, 2)].simplify()
print('Equation with respect to d^2 phi / dt^2')
display(eq2)

得られたeq1とeq2をdisplay関数で表示すると大変に複雑になるため，本記事では具体的な書き出しを割愛します。どちらかと言うと，eq1とeq2の式の形がどんなに複雑でも，実際のパラメータ（車輪や振り子の質量などの具体的な値）を代入して計算できることが重要です。このような場合，SymPyでの数式をまたNumPyで取り扱える関数に変換する，つまり，“Lambdify”すると便利です。Lambdifyした関数を用いてscipy.integrate.solve_ivp関数で取り扱える非線形状態方程式を定義します。Lambdifyした結果を用いたシミュレーションやアニメーションについては次回で取り扱います。

まとめ

思いの外長文になってしまいましたが，本記事ではまず，自由落下する質点を例題として，運動方程式をSymPy Mechanics（sympy.physics.mechanicsモジュール）を用いてシステマティックに導出しました。

本題の車輪形倒立振子は車輪と振り子という2つの剛体の運動となります。これらをSymPy MechanicsのRigidBodyオブジェクトとして定義し，位置，速度，拘束条件，位置エネルギーを設定することでラグランジアンを導出できますので，オイラー・ラグランジュ方程式から運動方程式を導出できます。結果として(18) ~ (21)式のように非常に複雑な運動方程式が得られますが，コンピュータで取り扱う上では複雑でも問題はないでしょう。

本来はこの後にSciPyを用いた数値シミュレーション，Matplotlibを用いたアニメーションまで書いていこうと考えておりましたが，長くなりましたので運動方程式の導出にフォーカスした記事として終え，シミュレーションとアニメーションについては次回で述べることとします。

付録

分散して記述していたPythonプログラムの全文を載せておきます。なお，display関数はJupyterLabでしか動作しませんので，1つの独立した.pyファイルとして実行したい場合は取り除くかprint関数に置き換えて下さい。

# ------------------------------------------------
# Derivation of the equation of motion
# of an inverted pendulum on a wheel
# (c) 2023 @RR_Inyo
# Released under the MIT license
# https://opensource.org/licenses/mit-license.php
# ------------------------------------------------

import sympy as sp
from sympy.physics.mechanics import *
init_vprinting()

# ------------------------------------------------
# Common symbols and reference frame
# ------------------------------------------------

# Define symbols, Common
t = sp.symbols('t')                                    # Time
g = sp.symbols('g')                                    # Gravity

# Define reference frame, Common
N = ReferenceFrame('N')
O = Point('O')                                         # Origin point
O.set_vel(N, 0)                                        # Origin point has zero velocity

# ------------------------------------------------
# Pendulum
# ------------------------------------------------

# Symbols
m, J_p, l, mu_p = sp.symbols('m J_p l mu_p')           # Mass, Inertia, length, and friction
theta = dynamicsymbols('theta')                        # Angle with respect to vertical line

# Reference frame and rigid body
A = N.orientnew('A', 'Axis', (theta, N.y))             # Define new reference frame for pendulum
A.set_ang_vel(N, theta.diff(t, 1) * N.y)               # Set angular velocity of reference frame
C_p = Point('C_p')                                     # Mass center of pendulum
J_p_tensor = J_p * outer(A.y, A.y)                     # Inertia tensor
P = RigidBody('P', C_p, A, m, (J_p_tensor, C_p))       # Definition of rigid body

# ------------------------------------------------
# Wheel
# ------------------------------------------------

# Symbols
M, J_w, a, mu_w = sp.symbols('M J_w a mu_w')
phi = dynamicsymbols('phi')

# Reference frame and rigid body
B = A.orientnew('B', 'Axis', (phi, A.y))               # Define new reference frame for pendulum
B.set_ang_vel(A, phi.diff(t, 1) * A.y)                 # Set angular velocity of reference frame
C_w = Point('C_w')                                     # Center of wheel
J_w_tensor = J_w * outer(B.y, B.y)                     # Intertia tensor
W = RigidBody('W', C_w, B, M, (J_w_tensor, C_w))       # Definition of rigid body

# ------------------------------------------------
# Constraints
# ------------------------------------------------

# Set positions
C_w.set_pos(O, a * ((theta + phi) * N.x + N.z))
C_p.set_pos(C_w, l * (sp.sin(theta) * N.x + sp.cos(theta) * N.z))

# Set velocities
C_w.set_vel(N, a * (theta.diff(t, 1) + phi.diff(t, 1)) * N.x)
C_p.set_vel(N, (a * (theta.diff(t, 1) + phi.diff(t, 1)) 
   + l * theta.diff(t, 1) * sp.cos(theta)) * N.x \
   - l * theta.diff(t, 1) * sp.sin(theta) * N.z)

# Point to apply disturbance
P_d = Point('P_d')
P_d.set_pos(C_p, l * A.z)
P_d.set_vel(N, (a * (theta.diff(t, 1) + phi.diff(t, 1)) \
    + 2 * l * theta.diff(t, 1) * sp.cos(theta)) * N.x \
    - 2 * l * theta.diff(t, 1) * sp.sin(theta) * N.z)

# ------------------------------------------------
# Kinetic energies
# ------------------------------------------------
print('Kinetic energy, Pendulum:')
display(P.kinetic_energy(N))

print('Kinetic energy, Wheel:')
display(W.kinetic_energy(N))

# ------------------------------------------------
# Potential energies
# ------------------------------------------------
P.potential_energy = m * g * l * sp.cos(theta)
print('Potential energy of pendulum:')
display(P.potential_energy)

# ------------------------------------------------
# Euler-Lagrange method
# ------------------------------------------------

# Get Lagrangian
L = Lagrangian(N, P, W)
print('Lagrangian:')
display(L)

# Generalized coordinate
q = [theta, phi]

# Generalized forces and torques
# Control torque
tau = sp.symbols('tau')
f_control = [(A, -tau * A.y), (B, tau * B.y)]

# Friction or dissipative
# Friction between pendulum and wheel
tau_fp = sp.symbols('tau_fp')
tau_fp = mu_p * phi.diff(t, 1)

# Friction between pendulum and wheel and friction between wheel and floor
tau_fw = sp.symbols('tau_fw')
tau_fw = -mu_p * phi.diff(t, 1) - mu_w * (theta.diff(t, 1) + phi.diff(t, 1))

f_dissipation = [(A, tau_fp * A.y), (B, tau_fw * B.y)]

# Disturbance force
f_d = sp.symbols('f_d')
f_disturbance = [(P_d, f_d * N.x)]

# Summation of generalized forces and torques
f = f_control + f_dissipation + f_disturbance

# Define a Lagrange's method
LM = LagrangesMethod(L, q, forcelist = f, frame = N)

# Derive equation of motion!
eom = LM.form_lagranges_equations()
print('Equation of motion:')
display(eom[0].simplify().factor())
display(eom[1].simplify().factor())

# ------------------------------------------------
# Angular acceleration
# ------------------------------------------------

# Solve equation of motion with respect to the second-order variables
sol = sp.solve(eom, [theta.diff(t, 2), phi.diff(t, 2)])

eq1 = sol[theta.diff(t, 2)].simplify()
print('Equation with respect to d^2 theta / dt^2')
display(eq1)

eq2 = sol[phi.diff(t, 2)].simplify()
print('Equation with respect to d^2 phi / dt^2')
display(eq2)

*1:台車を質点として取り扱っていました。

*2:ごくごく簡単な例でないと筆者の頭脳がパンクしてしまいます…😅

*3:後述しますが，倒立振子のように剛体を扱う場合は，それぞれの剛体が貼り付いている座標系を設定します。

*4:set_velはメソッドなのに，potential_energyは属性なのは不統一な感じがします…。

*5:オイラー・ラグランジュ方程式による運動方程式の導出過程そのものを表すオブジェクト

*6:y軸まわりにしか回転しないと限定しているのでこのような表現でも使えますが，任意の軸の周りの回転となると，もっとまじめに慣性モーメントテンソルを計算しないとダメでしょう。

*7:y軸まわりにしか回転しないと限定しているのでこのような表現でも使えますが，任意の軸の周りの回転となると，もっとまじめに慣性モーメントテンソルを計算しないとダメでしょう。

*8:厳密には車輪の半径aの分だけ高くなるはずですが，運動方程式を導出する際にzpで微分されて消えるので無視しました。

*9:なぜセッターを使わないのかな…。

*10:おかしょさんの「そらたまご」の記事では，振り子に対して働くトルクは零で，車輪のみにトルクが働くとして導出されています。また，「トルク」ではなく「モーメント」と呼んでいらっしゃいます。

*11:ただし，本当の転がり抵抗は速度（回転角速度）にあまり依存せず，逆に空気抵抗は速度の2乗に比例するようです。今後，場合によってはモデルの改善が必要かもしれません。

*12:積の順番などをSymPyの生の出力から筆者の好みで変えてあります。