The Negligible Lab

Astray in the forest of electrical and electronic circuits. Adrift in the gap between time and frequency domains. 独立独歩を是とする。

Pythonによる車輪形倒立振子の線形化と最適レギュレータ

制御工学 Python SymPy SciPy Matplotlib JupyterLab

はじめに

P計画

Pythonの数式処理ライブラリSymPyには力学系を取り扱うためのsympy.physics.mechanicsというモジュールがあります（以降，“SymPy Mechanics”とも呼びます）。本ブログでは前回，このSymPy Mechanicsの仕組みを活用して車輪形倒立振子の運動方程式を導出しました。

前回の最後に「次回はシミュレーションとアニメーションを扱う」と宣言していましたが，やはり，(i) 線形制御理論を活用した制御設計のためには線形化による状態空間モデルが必須であるとの思いから，また，(ii) SymPy Mechanicsには運動方程式を線形化する仕組みも備わっていることから，今回はまず線形化について記述することにします。その後，SymPyの結果をLambdifyなどによって数値化（具体的なパラメータ例を代入して，NumPyから活用できるようにすること）し，SciPyからこれを活用することによるシミュレーションとアニメーションについて述べていきます。

docs.sympy.org

ここまで来れば，実機の設計・製作の前に解決しておくべき課題は，加速度・ジャイロセンサの出力信号を用いた状態の推定と，DCモータのモデル化・制御になりますでしょうか。

完成イメージ

図1に完成したアニメーションを示します。図2に非線形な系である車輪形倒立振子の非線形な元のモデルとそれを線形化した状態空間モデル（「線形化モデル」とも呼ぶことにします）の挙動を重ねて表示したアニメーションを示します。車輪の質量M = 0.75 kg，車輪の半径a = 0.1 m，振り子の質量m = 1.5 kg，振り子の長さ2l = 0.6 mであり，車輪の初期位置xw0 = 1 m，振り子の初期角度θ0 = 15°の動きを可視化しています。よく見るとゴーストのように薄い色の車輪と振り子がほぼ重なって動いていますが，この色が薄い方が線形化モデルです。

図1: 車輪形倒立振子とその線形化モデルのアニメーションの例

ここでは線形化モデルに基づいて最適レギュレータ(LQR, linear quadratic regulator)の設計方法によって求めた状態フィードバックゲインを用いて倒立させており，時刻t = 5 sから0.5秒間のステップ状の外乱，時刻t = 8 sからの正弦波状の外乱にも負けずに倒立を維持している様子が見えますね。

時刻t = 15 s以降は制御を止めます。当たり前ですが振り子の倒立が維持できなくなり，非線形な元のモデルでは逆さまになってぶらぶらと振動します。一方の線形モデルでは高速回転しながらはるか彼方へふっ飛んでいきます。吉田勝俊先生の「短期集中：振動論と制御理論」（日本評論社，2003年）のp. 71の脚注にある通り，「線形化してしまったので，回転しないで発散する」を体現していますね。

いずれにしても本記事は筆者個人としての現代制御理論の初歩の学び直しのための備忘録のようなものであり，学術的に何ら新規性のある記述はしていませんのでご了承下さい。本記事独自の特長があるとすれば，SymPy Mechanicsの仕組みを活用した運動方程式の線形化の例題の1つとして，和文での記事である点，と言えるでしょうか。

目次

前回のおさらい

図2に車輪形倒立振子の全体図を示します。

図2: 車輪形倒立振子の全体図

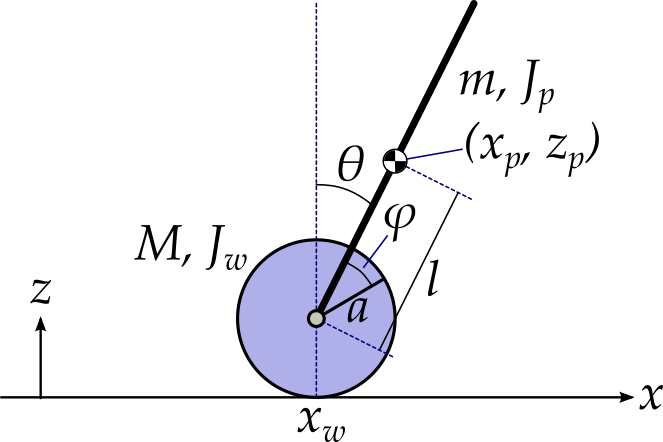
水平方向をx軸，鉛直方向をz軸とし，紙面（画面？）に垂直な方向をy軸とします。車輪形倒立振子の基本構造は，車輪の中心にピボットがあり，振り子の一端が取り付けられたものです。振り子にモータ等のトルク源を取り付け，車輪と振り子にトルクを加えることによって車輪の回転と振り子の倒立維持を図ります。

車輪の質量をM，半径をa，慣性モーメントをJw，車輪のx座標をxwとし，振り子の質量をm，長さを2l，重心の周りの慣性モーメントをJpとし，重心の座標を(xp, zp)とします。また，鉛直方向と振り子がなす角度をθ，振り子と車輪の基準動径のなす角をφとします。

前回，この車輪形倒立振子を対象として，SymPy Mechanicsの仕組みを活用し，オイラー・ラグランジュ方程式から運動方程式を導きました。ここでは該当部分のみのPythonコードを再掲します。ただし，振り子と車輪に相当する2つのRigidBodyオブジェクトPとWが貼り付いている座標系（ReferenceFrameオブジェクト）の名前を“A”，“B”から“N_p”，“N_w”にそれぞれ改名しました。と言うのも，後述する線形化の結果得られる行列の名前として“A”と“B”を使いたかったためです*1。

# ------------------------------------------------
# Euler-Lagrange method
# ------------------------------------------------

# Get Lagrangian
L = Lagrangian(N, P, W)
print('Lagrangian:')
display(L)

# Generalized coordinate
q = [theta, phi]

# Generalized forces and torques
# Control torque
tau = sp.symbols('tau')
f_control = [(N_p, -tau * N_p.y), (N_w, tau * N_w.y)]

# Friction or dissipative
# Friction between pendulum and wheel
tau_fp = sp.symbols('tau_fp')
tau_fp = mu_p * phi.diff(t, 1)

# Friction between pendulum and wheel and friction between wheel and floor
tau_fw = sp.symbols('tau_fw')
tau_fw = -mu_p * phi.diff(t, 1) - mu_w * (theta.diff(t, 1) + phi.diff(t, 1))

f_dissipation = [(N_p, tau_fp * N_p.y), (N_w, tau_fw * N_w.y)]

# Disturbance force
f_d = sp.symbols('f_d')
f_disturbance = [(P_d, f_d * N.x)]

# Summation of generalized forces and torques
f = f_control + f_dissipation + f_disturbance

# Define a Lagrange's method
LM = LagrangesMethod(L, q, forcelist = f, frame = N)

# Derive equation of motion!
eom = LM.form_lagranges_equations()
print('Equation of motion:')
display(eom[0].simplify().expand())
display(eom[1].simplify().expand())

結果として得られた運動方程式も再掲すると，以下のようになります（見やすさのため，上のコードの変数eomに格納されている生の形とは一部を括り出すなど変えてあります）。

\begin{align} \{ J_{w} &+ J_{p} + a^{2} (M + m) + m l (l + 2 a \cos \theta) \} \ddot{\theta} \\\ &+ \{J_{w} + a^{2} (M + m) + a m l \cos \theta\} \ddot{\phi} \\\ &- a m l \dot{\theta}^{2} \sin \theta - m g l \sin \theta \\\ &= -\mu_{w} (\dot{\theta} + \dot{\phi}) + (a + 2 l \cos \theta) f_{d} \end{align} \tag{1}
\begin{align} \{ J_{w} & + a^{2} (M + m) + a m l \cos \theta \} \ddot{\theta} \\\ &+ \{J_{w} + a^{2} (M + m)\} \ddot{\phi} - a m l \dot{\theta}^{2} \sin \theta \\\ &= \tau - \mu_{w} (\dot{\theta} + \dot{\phi}) - \mu_{p} \dot{\phi} + a f_{d} \end{align} \tag{2}

一見して分かる通り，状態変数のうち\theta，\dot{\theta}がsinやcosの中に入っていたり，2乗されていたりと，非線形であることは明白です（一方で\phiと\dot{\phi}の非線形性は弱いでしょうか）。以下では(1)，(2)式をSymPy Mechanicsの仕組みを活用することによって自動的に線形化，つまりは状態空間モデルを得て，最適レギュレータ(LQR, linear quadratic regulator)を作っていきます。

ここで，(1)，(2)式を最高次の微分である\ddot{\theta}と\ddot{\phi}の連立一次方程式とみなして解き，状態\boldsymbol{x}(t) = [\theta, \dot{\theta}, \phi, \dot{\phi}]^{T}と入力\boldsymbol{u}(t) = [\tau, f_{d}]^{T}に関する非線形状態方程式として，

\dot{\boldsymbol{x}}(t) = \boldsymbol{F}(\boldsymbol{x}(t), \boldsymbol{u}(t)) = \begin{bmatrix} F_{1} (\boldsymbol{x}(t), \boldsymbol{u}(t)) \\ F_{2} (\boldsymbol{x}(t), \boldsymbol{u}(t)) \\ F_{3} (\boldsymbol{x}(t), \boldsymbol{u}(t)) \\ F_{4} (\boldsymbol{x}(t), \boldsymbol{u}(t)) \end{bmatrix} \tag{3}

とも表現しておきましょう（誤解を生む恐れがなければ時刻tの関数であることを表す「(t)」を省略することもあります）。ただし，(3)式の一部は非常に単純な形をしていて，

\begin{align} F_{1} (\boldsymbol{x}(t), \boldsymbol{u}(t)) &= \dot{\theta} \\\ F_{3} (\boldsymbol{x}(t), \boldsymbol{u}(t)) &= \dot{\phi} \end{align} \tag{4}

です。残りのF_{2}(\boldsymbol{x}(t), \boldsymbol{u}(t))とF_{4}(\boldsymbol{x}(t), \boldsymbol{u}(t))は非常に複雑な形をしていますが，次のようにSymPyを使えば求めることができます。

# ------------------------------------------------
# Angular acceleration
# ------------------------------------------------

# Solve equation of motion with respect to the second-order variables
sol = sp.solve(eom, [theta.diff(t, 2), phi.diff(t, 2)])

eq1 = sol[theta.diff(t, 2)].simplify()
print('Equation with respect to d^2 theta / dt^2')
display(eq1)

eq2 = sol[phi.diff(t, 2)].simplify()
print('Equation with respect to d^2 phi / dt^2')
display(eq2)

ただし，非常に複雑であるため，具体的に書き出すことは割愛させて頂きます。ここで得られたeq1とeq2については，後述のようにLambdifyして数値シミュレーションに用います。

運動方程式の線形化

運動方程式の線形化については，台車形倒立振子を対象として本ブログの前々回でも一応は取り扱っています。ここで「一応は」と付けた理由は，SymPyの仕組みをフル活用していなかったことにあります。今回はSymPy Mechanicsに備わっている機能を活用して，自動的に，あるいは体系的に運動方程式を線形化することを試みます。

線形化に関する一般論のおさらい

前々回のおさらいですが，一般的な非線形状態方程式とその線形化を考えてみましょう。まず，状態\boldsymbol{x}(t)を

\boldsymbol{x}(t) = [x_{1}(t), x_{2}(t), \dots, x_{n}(t) ]^{T} \tag{5}

また，入力\boldsymbol{u}(t)を

\boldsymbol{u}(t) = [u_{1}(t), u_{2}(t), \dots, u_{m}(t) ]^{T} \tag{6}

とする非線形なシステムがあり，その（非線形）状態方程式を

\dot{\boldsymbol{x}}(t) = \boldsymbol{F}(\boldsymbol{x}(t), \boldsymbol{u}(t)) = \begin{bmatrix} F_{1}(\boldsymbol{x}(t), \boldsymbol{u}(t)) \\ F_{2}(\boldsymbol{x}(t), \boldsymbol{u}(t)) \\ \vdots \\ F_{n}(\boldsymbol{x}(t), \boldsymbol{u}(t)) \end{bmatrix} \tag{7}

と書けるものとします。

これを平衡点の周りで線形化することを考えます。状態\boldsymbol{x}(t)を平衡点と微小変動に分け，

\boldsymbol{x}(t) = \boldsymbol{X} + \Delta \boldsymbol{x}(t) = [X_{1} + \Delta x_{1}(t), X_{2} + \Delta x_{2}(t), \dots, X_{n} + \Delta x_{n}(t) ]^{T} \tag{8}

のように書くとします。同様に，入力\boldsymbol{u}(t)についても，

\boldsymbol{u}(t) = \boldsymbol{U} + \Delta \boldsymbol{u}(t) = [U_{1} + \Delta u_{1}(t), U_{2} + \Delta u_{2}(t), \dots, U_{m} + \Delta u_{m}(t) ]^{T} \tag{9}

と表すものとします。これらについて“\Delta”の付いた微小変動分のみを取り出せば，

\Delta \boldsymbol{x}(t) = [\Delta x_{1}(t), \Delta x_{2}(t), \dots, \Delta x_{n}(t) ]^{T} \tag{10}

また，

\Delta \boldsymbol{u}(t) = [\Delta u_{1}(t), \Delta u_{2}(t), \dots, \Delta u_{m}(t) ]^{T} \tag{11}

ですね。

ここで，微小変動分\Delta \boldsymbol{x}(t)，\Delta \boldsymbol{u}(t)に着目して(7)式を線形近似すると次式のように書けます。

\Delta \dot{\boldsymbol{x}}(t) = \boldsymbol{A} \Delta \boldsymbol{x}(t) + \boldsymbol{B} \Delta \boldsymbol{u}(t) \tag{12}

ただし，

\boldsymbol{A} = \begin{bmatrix} \displaystyle \frac{\partial F_{1}}{\partial x_{1}} & \displaystyle \frac{\partial F_{1}}{\partial x_{2}} & \dots & \displaystyle \frac{\partial F_{1}}{\partial x_{n}} \\[5pt] \displaystyle \frac{\partial F_{2}}{\partial x_{1}} & \displaystyle \frac{\partial F_{2}}{\partial x_{2}} & \dots & \displaystyle \frac{\partial F_{2}}{\partial x_{n}} \\[5pt] \vdots & \vdots & \ddots & \vdots \\[5pt] \displaystyle \frac{\partial F_{n}}{\partial x_{1}} & \displaystyle \frac{\partial F_{n}}{\partial x_{2}} & \dots & \displaystyle \frac{\partial F_{n}}{\partial x_{n}} \end{bmatrix}_{(\boldsymbol{x}, \boldsymbol{u}) = (\boldsymbol{X}, \boldsymbol{U})} \tag{13}

また，

\boldsymbol{B} = \begin{bmatrix} \displaystyle \frac{\partial F_{1}}{\partial u_{1}} & \displaystyle \frac{\partial F_{1}}{\partial u_{2}} & \dots & \displaystyle \frac{\partial F_{1}}{\partial u_{m}} \\[5pt] \displaystyle \frac{\partial F_{2}}{\partial u_{1}} & \displaystyle \frac{\partial F_{2}}{\partial u_{2}} & \dots & \displaystyle \frac{\partial F_{2}}{\partial u_{m}} \\[5pt] \vdots & \vdots & \ddots & \vdots \\[5pt] \displaystyle \frac{\partial F_{n}}{\partial u_{1}} & \displaystyle \frac{\partial F_{n}}{\partial u_{2}} & \dots & \displaystyle \frac{\partial F_{n}}{\partial x_{m}} \end{bmatrix}_{(\boldsymbol{x}, \boldsymbol{u}) = (\boldsymbol{X}, \boldsymbol{U})} \tag{14}

です。言い換えれば，線形化された状態空間モデルの\boldsymbol{A}行列，\boldsymbol{B}行列は，元の非線形状態方程式を表すベクトル値関数\boldsymbol{F}(\boldsymbol{x}(t), \boldsymbol{u}(t))の平衡点でのヤコビアンであるとも言えます。

sympy.physics.mechanicsによる運動方程式の線形化

台車形倒立振子を取り扱った前々回は(13)，(14)式のようなヤコビアンを計算するにあたって，SymPyのdiffメソッドとsubsメソッドを使ってひとつひとつの要素を個別に計算していました。しかし，SymPy Mechanicsには運動方程式を線形化する機能が備わっていますので，今回はその機能を活用することとしました。

ラグランジュ法によって運動方程式を導出する箇所のPythonプログラムを抜粋再掲します。

# Define a Lagrange's method
LM = LagrangesMethod(L, q, forcelist = f, frame = N)

# Derive equation of motion!
eom = LM.form_lagranges_equations()

LagrangesMethodオブジェクトであるLMに対してlinearizeというメソッドを適用することで，自動的，体系的かつ容易に線形化が可能です。具体的には下記のように書きます。

# ------------------------------------------------
# Linearization
# ------------------------------------------------

# Set operating point
op_point = {theta: 0, theta.diff(t, 1): 0, phi: 0, phi.diff(t, 1): 0}

# Linearize!
kwargs = {'q_ind': [theta, phi], 'qd_ind': [theta.diff(t, 1), phi.diff(t, 1)], \
          'A_and_B': True, 'op_point': op_point, 'simplify': True}
A, B, inp_vec = LM.linearize(**kwargs)

まず，op_pointという辞書を作り，運動方程式を線形化する動作点(operating point)を定義します。この「動作点」は必ずしも「平衡点」でなくても構わないようですが，ここではやはり，振り子が倒立して静止，かつ，車輪が原点にあって静止しており，制御トルクも外乱力もない状態，すなわち

\boldsymbol{X} = [0, 0, 0, 0]^{T}, \qquad \boldsymbol{U} = [0, 0]^{T} \tag{15}

を動作点とします。これをop_pointという辞書型変数にて6行目のように定義します。

次にLMに対してlinearizeというメソッドを適用するのですが，ここでは引数をあらかじめkwargsという辞書にキーワード引数として定義しておくことにしました。q_indは一般化座標，qd_indは一般加速度です。A_and_BをTrueに設定しています。この場合，(12) ~ (14)式のような表現形式のA行列とB行列を得られます。一方，Falseにしておくと，M，A，Bの3つの行列が得られ，恐らくですがディスクリプタ形式と言われる書き方になるのではないかと思います。

次に，op_pointとしてop_pointを渡します。動作点ですね。最後にsymplifyをTrueとします。これはA，B行列の各要素をSymPyのルールに従って整理，単純化することを意味します。

最後の行でA, B, inp_vec = LM.linearize(**kwargs)として線形化の計算を実行します。返り値はそれぞれA行列，B行列，それからinp_vecという変数に入ります。

さて，これまでの議論で(12)式の\Delta \boldsymbol{u}(t)に相当する「入力」について定義していませんでした。どうやって\Delta \boldsymbol{u}(t)に含まれるシンボルを指定するのかと思っていたところ，公式ドキュメントに下記の記述を見付けました。

The additional output inp_vec is a vector containing all found dynamicsymbols not included in the generalized coordinate or speed vectors. These are assumed to be inputs to the system, forming the \boldsymbol{r} vector described in the background above.

少し分かり難いですが，SymPyの公式ドキュメントでは入力を“\boldsymbol{u}”ではなく“\boldsymbol{r}”と表記しています（“\boldsymbol{u}”は一般加速度としているようです）。linearizeメソッドはどのシンボルが入力であるかについて，一般化座標(q_ind)や一般加速度(qd_ind)に含まれておらず，かつ，dynamicsymbolsとして定義されているシンボルを入力と見なすようです。しかし，前回までは制御トルクtauも外乱力f_dもただのシンボルとしてしまっていました。プログラムからtau，f_dの元の定義を削除し，かつ，

tau = dynamicsymbols('tau')
f_d = dynamicsymbols('f_d')

の2行を書き加えておきましょう。

いよいよLM.linearizeメソッドを実行すると，A，B，inp_vecを得ます。次のようにJupyterLabに入力して結果を確認してみましょう。

# ------------------------------------------------
# Results of linearization
# ------------------------------------------------
print('A =')
display(A)

print('B =')
display(B)

print('inp_vec =')
display(inp_vec)

A行列，B行列ともに複雑な形になりますので，ここで具体的に書き出すことは割愛させて頂きます。代わりに，図3としてJupyterLabの画像を貼り付けますのでご覧ください。

図3: 線形化の結果をJupyterLabで確認（スクリーンショット）
ご覧の通りA行列，B行列の要素には相当に複雑なものもありますが，ここでは具体的な式の形を追うことはせず，後述のようにSymPyでの行列表現をNumPyの配列(ndarray)に変換して最適レギュレータの設計や数値シミュレーションに活用します。

なお，得られたA，B行列も入力ベクトルinp_vecに関しても，前回から本記事で考えている要素とは順番が異なっています。前回から本記事の後述のプログラムでは状態\boldsymbol{x} = [\theta, \dot{\theta}, \phi, \dot{\phi}]^{T}と入力\boldsymbol{u} = [\tau, f_{d}]^{T}と考えていましたが，ここで得られたA，B，inp_vecについては，状態\boldsymbol{x} = [\theta, \phi, \dot{\theta}, \dot{\phi}]^{T}と入力\boldsymbol{u} = [f_{d}, \tau]^{T}となっています。したがって後述のように行と列を入れ替えます。

数値解析への準備

具体的なパラメータの代入

以上で運動方程式の導出と線形化について述べて参りましたが，以下では各パラメータに具体的な数値を代入して数値解析，数値シミュレーションに進みます。まずは必要なライブラリ・モジュールをインポートしておきます。

import numpy as np
from scipy.linalg import solve_continuous_are
from scipy.integrate import solve_ivp
import scipy.constants as cnst

例として振り子の質量m = 1.5 kg，振り子の長さ2l = 60 cm，振り子と車輪の摩擦に関する減衰係数μp = 0.05 N/(rad/s)とし，車輪の質量M = 0.75 kg，車輪の半径a = 0.1 m，車輪と床面の摩擦に関する減衰係数μw = 0.05 N/(rad/s)とします。振り子を一様な細い棒と考えると，振り子の重心の周りの慣性モーメントJp = ml2 / 3となり，車輪を円板と考えると慣性モーメントJw = Ma2 / 2となります。 これらのパラメータを以下のPythonプログラムのように設定しますが，具体的な数値を代入する変数にはすべてアンダーバー(“_”)を付しています。と言うのも，SymPyで既にm，Mなどの変数名を使用してしまっているためです。

# ------------------------------------------------
# Numerical parameter examples
# ------------------------------------------------

# Reset format
np.set_printoptions(formatter = None)

# Pendulum
_m = 1.50                    # Mass of pendulum, kg
_l = 0.30                    # Half length of pendulum, m
_J_p = _m * _l**2 / 3        # Inertia of pendulum
_mu_p = 0.05                 # Friction of pendulum, N/(rad/s)

# Wheel
_M = 0.75                    # Mass of wheel, kg
_a = 0.10                    # Radius of wheel, m
_J_w = _M * _a**2 / 2        # Inertia of wheel, kg m**2
_mu_w = 0.05                 # Friction of wheel, N/(rad/s)

# Gravity
_g = cnst.g                  # Gravity on Earth, m/s**2

なお，重力加速度gについてはscipy.constantsからインポートしました。

非線形状態方程式のLambdificationと定義

まず，元の非線形なシステムを数値シミュレーションするため，(3)式に示した非線形状態方程式のうち，複雑な形となるF_{2}(\boldsymbol{x}(t), \boldsymbol{u}(t))とF_{4}(\boldsymbol{x}(t), \boldsymbol{u}(t))をNumPyで計算できるようにLambdifyします。

# ------------------------------------------------
# Lambdification of SymPy results
# ------------------------------------------------

# Give derivatives new name
theta_dot, phi_dot = sp.symbols('theta_dot phi_dot')

# Definition of the lambdified functions
_eq1 = eq1.subs([(theta.diff(t, 1), theta_dot), (phi.diff(t, 1), phi_dot), \
    (m, _m), (l, _l), (J_p, _J_p), (M, _M), (a, _a), (J_w, _J_w), \
    (mu_p, _mu_p), (mu_w, _mu_w), (g, _g)])

func_eq1 = sp.lambdify([theta, theta_dot, phi, phi_dot, tau, f_d], \
    _eq1, 'numpy')

_eq2 = eq2.subs([(theta.diff(t, 1), theta_dot), (phi.diff(t, 1), phi_dot), \
    (m, _m), (l, _l), (J_p, _J_p), (M, _M), (a, _a), (J_w, _J_w), \
    (mu_p, _mu_p), (mu_w, _mu_w), (g, _g)])

func_eq2 = sp.lambdify([theta, theta_dot, phi, phi_dot, tau, f_d], \
    _eq2, 'numpy')

前章で得たeq1とeq2について，subsメソッドを用いて各パラメータに具体的な値を代入します（アンダーバーなしの変数をアンダーバーありの変数に置き換えます）。さらに，sympy.lambdify関数を用いてNumPyで計算できる関数func_eq1とfunc_eq2を生成します。これら2つの関数の引数はtheta, theta_dot, phi, phi_dot, tau, f_dの6つです。前者4つが状態変数\boldsymbol{x}，後者2つが入力\boldsymbol{u}ですね。

線形化した状態方程式のA，B行列の数値化と定義

一方，線形化した状態方程式のA，B行列についても，具体的なパラメータの値を代入して数値計算できるようにします。sympy.matrix2numpyという関数を用いて，SymPyの行列をNumPyの配列(ndarray)に変換できます*2。まず，AやBに対してsubsメソッドで各パラメータに具体的な値を代入します（アンダーバーなしの変数をアンダーバーありの変数に置き換えます）。その後，matrix2numpy関数で配列に変換しますが，ここで，データタイプをdtype = 'float64'として明示的に設定しておきます。そうでなければデフォルトでdtype=<class 'object'>となってしまい，その後の計算でエラーが出てしまうことがありました。AとBという変数名はSymPyでの行列に使用されてしまっているので，数値化したA，B行列はアンダーバーを加えて，_A，_Bとします。

# ------------------------------------------------
# Linearization results to NumPy arrays, A and B
# ------------------------------------------------

# NOTE:
#  x = [theta, phi, theta_dot, phi_dot]^T
#  u = [f_d, tau]^T

# The A matrix
_A_tmp = sp.matrix2numpy(A.subs([(m, _m), (l, _l), (J_p, _J_p), (M, _M), \
    (a, _a), (J_w, _J_w), (mu_p, _mu_p), (mu_w, _mu_w), (g, _g)]), \
    dtype = 'float64')

# The B matrix
_B_tmp = sp.matrix2numpy(B.subs([(m, _m), (l, _l), (J_p, _J_p), (M, _M), \
    (a, _a), (J_w, _J_w), (mu_p, _mu_p), (mu_w, _mu_w), (g, _g)]), \
    dtype = 'float64')

# Change raw and column orders to fit existing routines
_A_tmp = _A_tmp[[0, 2, 1, 3], :]
_A = _A_tmp[:, [0, 2, 1, 3]]
print(f'A = \n{_A}')

_B_tmp = _B_tmp[[0, 2, 1, 3], :]
_B = _B_tmp[:, [1, 0]]
print(f'B = \n{_B}')

20行目以降で，A，Bの行や列を入れ替え，状態変数や入力の順番を前回から本記事までに作成しておいたプログラムと合致するようにしています。

最適レギュレータ

最適レギュレータの一般論

線形化した状態方程式に基づいて最適レギュレータを作ります。次式で表される評価関数Jを最小化するコントローラを最適レギュレータ(LQR, linear quadratic regulator)といいます。

J = \displaystyle \int_{0}^{\infty} \left (\boldsymbol{x}^{T} (t) \boldsymbol{Q} \boldsymbol{x} (t) + \boldsymbol{u}^{T} (t) \boldsymbol{R} \boldsymbol{u} (t) \right ) dt \tag{16}

ただし，\boldsymbol{Q} (= \boldsymbol{Q}^{T} > 0)は状態\boldsymbol{x}に関する重み行列，\boldsymbol{R} (= \boldsymbol{R}^{T} > 0)は入力\boldsymbol{u}に関する重み行列です。最適レギュレータの状態フィードバックゲイン\boldsymbol{F}_{\mathrm{opt}}は，

\boldsymbol{F}_{\mathrm{opt}} = -\boldsymbol{R}^{-1} \boldsymbol{B}^{T} \boldsymbol{P} \tag{33}

として得ることができます。ただし，\boldsymbol{P} (= \boldsymbol{P}^{T} > 0)はRiccati方程式

\boldsymbol{A}^{T} \boldsymbol{P} + \boldsymbol{P} \boldsymbol{A} + \boldsymbol{P} \boldsymbol{B} \boldsymbol{R}^{-1} \boldsymbol{B}^{T} \boldsymbol{P} + \boldsymbol{Q} = 0 \tag{34}

の解です（どうしてこうなるのか，筆者はまったく理解していません…💧）。(16)式を見ると，状態\boldsymbol{x}(t)が素早く零に収束すること，また，入力\boldsymbol{u}(t)が小さくなることによって，評価関数Jが小さくなります。状態\boldsymbol{x}(t)の収束（\boldsymbol{x}の要素であるそれぞれの状態変数毎の収束）と入力\boldsymbol{u}(t)が大きくならないこと（車輪形倒立振子では振り子と車輪に加える制御トルクが大きくなりすぎないこと）のいずれを重視するかで\boldsymbol{Q}と\boldsymbol{R}に設定する値を変えると，自動的にその目的に合致する状態フィードバックゲインが求まります。

「最適」と言っても「何について最適であるか」は重み\boldsymbol{Q}，\boldsymbol{R}で決まりますので，結局，\boldsymbol{Q}と\boldsymbol{R}を変えてみるという試行錯誤は必要かと思われます。ただし，これでも状態フィードバックゲインを直接変えて試行錯誤するよりはるかに効率的です。というのも，（線形化モデルに対してであれば）必ず制御できる状態フィードバックゲインが選ばれるからです（状態フィードバックゲインを直接あれこれしていると，制御できない組み合わせとなることがあり得ます）。なお，車輪形倒立振子のように（制御としては）1入力である場合，\boldsymbol{R}はスカラーになります。

最適レギュレータの例

例として，次のような最適レギュレータを設計してみます。SciPyのsolve_continuous_are関数を使ってRiccati方程式を解くことができます。B行列については制御力の部分のみを考慮するので_Bの1列目のみをスライスして_B_cを生成しています。重み行列_Qとしては，diagを使って対角成分のみをもつ行列を定義しています。_Q11 = 35，_Q33 = 2として，1つ目の状態変数，すなわち振り子の角度θを重視する重みを設定しました。また，_R = [20]を設定して，入力が大きくならないようにしました（試行錯誤です）。

# ------------------------------------------------
# LQR, linear quadratic regulator
# ------------------------------------------------
# Weights
_B_c = np.array([_B[:, 0]]).T    # As a column vector here
_Q = np.diag([35, 0, 2, 0])
_R = np.array([[20]])

# Solve Riccati equation
_P = solve_continuous_are(_A, _B_c, _Q, _R)
_F = (-np.linalg.inv(_R) @ _B_c.T @ _P)[0]
print(f'State-feedback gain _F =\n{_F}\n')

# Check eigenvalues of closed-loop system
w_lqr, v_lqr = np.linalg.eig(_A + _B_c * _F)
print(f'Eigenvalues of closed-loop system =\n{w_lqr}')

この条件で10行目のようにRiccati方程式の解_Pを求めます。さらに次の行で_Pから状態フィードバックゲイン_Fを得ています。最後にprint関数で_Fと，閉ループ系の固有値を表示しますが，その出力は以下となります。

State-feedback gain _F =
[8.15993077 1.78704447 0.31622777 0.30764017]

Eigenvalues of closed-loop system =
[-9.59854739+0.j         -7.70770041+0.j         -2.45817597+0.97135982j
 -2.45817597-0.97135982j]

閉ループ系の固有値の実部はすべて負になっており，安定化できていることが判ります。以上で状態フィードバックゲインが得られました。

前々回は最適レギュレータの例を2つ作って比較してみましたが，今回は1つの例だけで勘弁して下さい…😅 基本的な考え方は同様です。

シミュレーションとアニメーション

以上で準備したfunc_eq1，func_eq1や_A，_B行列，さらに状態フィードバックゲイン_Fを用いて，SciPyによる数値シミュレーションを実行してみます。また，Matplotlibによるアニメーションも生成します。

非線形および線形状態方程式の定義

非線形バージョン

非線形状態方程式をSciPyのsolve_ivp関数で解くための関数を定義します。なお，10行目でtorque_control関数を，また，13行目でforce_disturbance関数をそれぞれ呼び出していますが，これらについては後述します。

# ------------------------------------------------
# Non-linear state-space equation
# ------------------------------------------------
def func(t, x):
    # Extract state variables
    # State variable x = [theta, theta_dot, phi, phi_dot]^T
    theta, theta_dot, phi, phi_dot = x
    
    # Torque for control
    tau = torque_control(t, x)
    
    # Disturbance
    f_d = force_disturbance(t, x)
    
    # Calculate derivative of state x
    dxdt = np.zeros_like(x)
    dxdt[0] = theta_dot
    dxdt[1] = func_eq1(theta, theta_dot, phi, phi_dot, tau, f_d)
    dxdt[2] = phi_dot
    dxdt[3] = func_eq2(theta, theta_dot, phi, phi_dot, tau, f_d)
    
    # Return result
    return dxdt

前々々回*3において台車形倒立振子をシミュレーションした場合においては，この関数内に複雑な非線形状態方程式を直接書いていましたが，今回は18，20行目に示す通り，Lambdifyした結果であるfunc_eq1とfunc_eq2を呼んでいます。SymPyの結果を直接利用しているため，デバッグなどで運動方程式の形を見直した場合にも使えるようになっています。

線形バージョン

線形化と数値化の結果として得られたNumPyの配列(ndarray)であるA，Bを用いた状態方程式をてSciPyのsolve_ivp関数で解くための関数を定義します。なお，10行目でtorque_control関数を，また，13行目でforce_disturbance関数をそれぞれ呼び出していますが，これらについては後述します。

# ------------------------------------------------
# Linearized state-space equation
# ------------------------------------------------
def func_lin(t, x):
    # Extract state variables
    # State variable x = [theta, theta_dot, phi, phi_dot]^T
    theta, theta_dot, phi, phi_dot = x
    
    # Torque for control
    tau = torque_control(t, x)
    
    # Disturbance
    f_d = force_disturbance(t, x)
    
    # Input vector
    u = np.array([tau, f_d])
    
    # Calculate derivative of state x
    dxdt = _A @ x + _B @ u
    
    # Return result
    return dxdt

これはシンプルですね。特に19行目では@演算子の力によってほぼ数式通りの表記となっています。なお，7行目で各状態変数(theta, theta_dot, phi, phi_dot)をxから取り出していますが，今の状態ではこれらは使用していません。

制御トルクを生成するtorque_control関数

状態フィードバックによって制御トルクを生成する関数を定義します。引数は時刻tと状態xです。時刻t < 15 sまでは状態フィードバックを続け，t ≥ 15 sとなったら制御を止めてトルクを零とするようにしました。制御を止めると振り子の倒立を維持できなくなり，倒れて下向きになってブラブラするはずです。

# ------------------------------------------------
# Torque for control
# ------------------------------------------------

# State feedback gain, obtained by linearization and LQR!
F = _F

# Maximum torque, Nm
tau_max = 3

def torque_control(t, x):
    # State variable x = [theta, theta_dot, phi, phi_dot]^T
    theta, theta_dot, phi, phi_dot = x
    if t < 15:
        # State-feedback control
        tau = np.clip(F @ x, -tau_max, tau_max)

    else:
        # Stop controlling
        tau = 0
   
    return tau

9行目でtau_max = 3として最大トルクを3 Nmに制限するようにしました。現実のモータは無限大のトルクを生成できるわけではないので，このような制限があるはずです。

外乱力を生成するforce_disturbance関数

外乱力については以下のように定義しました。時刻t = 5 sから1秒間にわたって5 Nの力を振り子の先端に加えます。また，時刻t = 8 sから3秒間にわたって振幅5 Nで正弦波状の外乱を振り子の先端に加えます。それ以外の時間帯では外乱を零とします。

# ------------------------------------------------
# Disturbance force
# ------------------------------------------------
def force_disturbance(t, x):
    # State variable x = [theta, theta_dot, phi, phi_dot]^T
    if 5 <= t < 6:
        f_d = 5
    elif 8 <= t < 11:
        f_d = 5 * np.sin(2 * np.pi * 1 * (t - 9))
    else:
        f_d = 0
    
    return f_d

非線形および線形状態方程式を解く

SciPyのsolve_ivp関数を用いて非線形および線形状態方程式の初期値問題を解きます。基本的な考え方は本ブログで何度か取り扱った通りです。

# ------------------------------------------------
# Solution of non-lin. and lin dynamics by SciPy
# ------------------------------------------------

# NumPy array for time
t_end = 20                        # Time to end simulation, s
dt = 0.01                         # Time slice, s
_t = np.arange(0, t_end, dt)      # Time array

# Initial conditions
theta_0 = np.radians(15)          # Initial pendulum angle, rad
x_w0 = 1                          # Initial wheel positon, m
phi_0 = x_w0 / _a - theta_0       # Initial wheel angle with respect to pendulum
x0 = [theta_0, 0, phi_0, 0]       # Initial state

# Now solve it, non-linear
sol = solve_ivp(func, [0, t_end], x0, t_eval = _t)

# Now solve it, linearized
sol_lin = solve_ivp(func_lin, [0, t_end], x0, t_eval = _t)

ここではt_end = 20として20秒間の現象を解くこととし，dt = 0.01として時間刻みを10 msに設定します。ここでは振り子の初期角度θ0= 15°，車輪の初期位置xw = 1 mとなるようにφ0を設定し，solve_ivp関数にて非線形，線形の状態方程式を解き，結果をそれぞれsolとsol_linという変数に格納しています。

得られたsolとsol_linはそのままでは使い勝手が悪いので，後処理として次のようなことをしています。非線形バージョンを代表として示しますが，線形バージョンも同様です。また，求解の結果得られた状態の時刻歴から改めて制御トルク_tau_contと外乱_f_dの時刻歴をそれぞれ生成し直しています。これは，これらの信号についてsolve_ivp関数の計算中には（筆者のスキルでは）取り出せないためです。

# ------------------------------------------------
# Post-processing of the solution, non-linear
# ------------------------------------------------

# State variables
_theta = (sol.y[0,:].T + np.pi) % (2 * np.pi) - np.pi
_theta_dot = sol.y[1,:].T
_phi = (sol.y[2,:].T + np.pi) % (2 * np.pi) - np.pi
_phi_dot = sol.y[3,:].T

# Position and velocity of wheel, theta + phi
_x_w = _a * (sol.y[0,:].T + sol.y[2,:].T)
_v_w = _a * (sol.y[1,:].T + sol.y[3,:].T)

# Reproduce control torque and disturbance force
_tau_cont = np.zeros_like(_t)
_f_d = np.zeros_like(_t)
for i, __t in enumerate(_t):
    _tau_cont[i] = torque_control(__t, sol.y[:,i])
    _f_d[i] = force_disturbance(__t, sol.y[:,i])

時間波形を見る

求解できたら時間波形を見てみます。図4にMatplotlibでプロットした波形を示します。

図4: 車輪形倒立振子とその線形化モデルの時間波形の例
青が元の非線形なシステム，橙が線形化モデルですが，良好な一致が見られます。制御を止めた時刻t = 15 s以降では振り子が倒れてしまうので相違が目立ちます。と言うか，線形化モデルは使えなくなります。

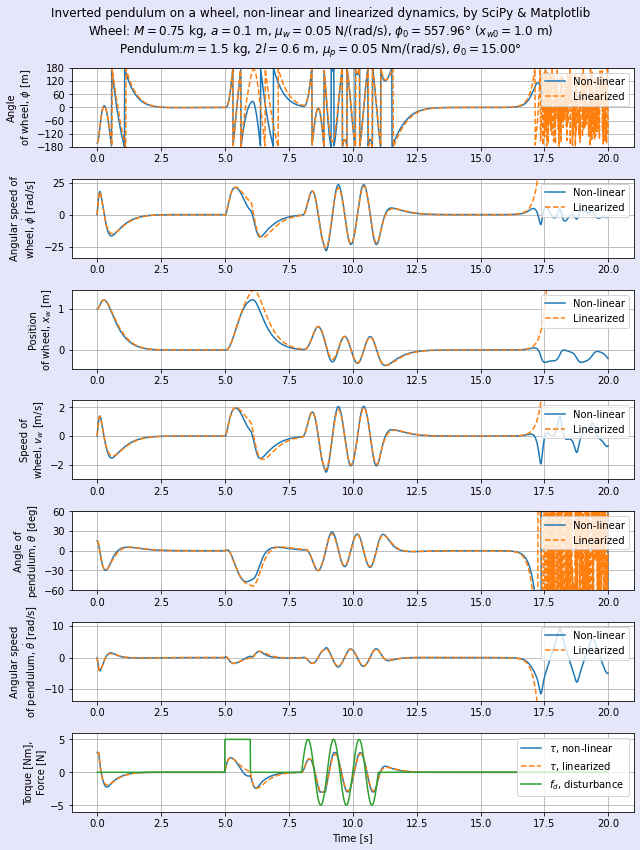
しかしこれでは実際にどのような挙動か分かり難いので，やはりアニメーションで可視化するのが有用でしょう。

アニメーションの生成

アニメーションの生成に関するPythonのプログラムについては長くなってしまうため，ここでは割愛させて頂きます。前々々回など，本ブログでは何度か取り扱っており，基本的な考え方は全く同じです。

図5: 車輪形倒立振子とその線形化モデルのアニメーションの例（図1の再掲）
図5に生成したアニメーションを示します。これは図1の再掲です。

状態フィードバックゲインを直接トライ・アンド・エラーで弄っていた前回と比べると，やはり最適レギュレータを用いた制御となっている今回はスッと原点に戻るようになっていますね。

まとめ

結論

以上でSymPyに備わっている機能として，LagrangesMethodオブジェクトのlinearizeメソッドを用いた車輪形倒立振子の運動方程式の線形化について述べました。動作点を指定してこのlinearizeメソッドを実行すると，線形な状態空間モデルのA行列とB行列が得られます。

また，元の非線形モデルと線形化した状態方程式（線形化モデル）に具体的なパラメータの例を代入し，線形化モデルに基づいて最適レギュレータ(LQR, linear quadratic regulator)を作りました。さらに，SciPyのsolve_ivp関数を用いて初期値問題として解き，結果をアニメーションとして可視化しました。

ブログの記述としては非常に駆け足だったので，見る価値もない駄文となっているのではないかと危惧しております。

今後の課題

冒頭にも述べた通り，今のところ見えている残る課題は，加速度・ジャイロセンサの出力信号を用いた状態の推定と，DCモータのモデル化・制御となると考えています。前者については導出したSymPyの運動方程式から加速度・ジャイロセンサを取り付ける箇所の加速度と重力加速度からある程度計算で見えてくるのではないかと漠然と予想していますが，TDK InvenSense MPU6050など，実際のセンサを用いた予備実験なども必要かもしれませんね。

後者については，タミヤ模型のミニ四駆などに使われているいわゆる130モータのモデル化を試みます。これも予備実験が必要でしょう。もし，実機の倒立振子においてモータのトルクや速度，パワーが不足したら，ハイパーダッシュモーターでも採用してみましょうか…！

なかなか歩みは遅く，今年も5月が後半に入ってまいりました。願わくば今年中に実機の車輪形倒立振子を立たせたいと思っています。

*1:前回のコーディング時にもっと先見の明があればこんなことには…💧

*2:numpy.matrixではないことに注意が必要です。

*3:RADWIMPS感あり。