LTspiceで三相PWM整流器を作る ~d-q座標系編~
はじめに
秋分を過ぎ,本格的に季節が巡って参りましたね🍂 前記事よりまた間が空いてしまいましたが,三相PWM整流器の直流電圧制御について,私の理解が非常に浅かったことが分かり,改めて考え直していたところです。 本記事では,まず,前記事で宿題となっていたd-q座標系での等価回路を導出します。 本題である直流電圧制御系とその安定性については,長くなりそうなので次記事に譲ることとします。
何を導出したいか
ここでは,系統と変換器が抵抗とインダクタンスを介して向き合っている三相回路をd-q座標系で表現した等価回路を導出します。 図1に三相PWM整流器(単線図)とフェーザ図を示します。

スイッチング周波数成分を無視し,電圧形インバータ部分も正弦波と見なして3線図とすれば,図2(a)の等価回路を得ます。 図2(b), (c)はd-q座標系での等価回路(d軸・q軸等価回路)です。これはどのように導出するのでしょうか? d軸とq軸の干渉項である−ωLiqやωLidは一体どこから出てくるのか…?

なお,本記事では三相等価回路である図2(a)から出発し,座標変換にて図2(b), (c)が得られることを示しますが, α-β変換(Clarke変換)やd-q変換(Park変換)そのものの概念や効用については記載していません…💦 アニメーションを使った説明が秀逸なMathWorksさんの記事へのリンクを貼っておきます。
続きを読むLTspiceで三相PWM整流器を作る ~モデル作成編~
はじめに
前記事から間が開いてしまいました。もう秋に入りつつありますが,まだまだ暑い日が続いていますね。 本記事では,LTspiceで三相PWM整流器(回生もできるので,一般の三相系統連系変換器*1として考えてください)を作った過程を書いてみました。
自作制御ライブラリの活用例として
さて,前記事を書き終えた後,LTspice向けに開発中の自作制御ライブラリContrailleの活用例の1つとして,三相PWM整流器を作ることにしました。 LTspiceというと,「オペアンプ等のアナログ回路やスイッチング電源のシミュレーションに使うもの」というイメージがありますが,系統連系変換器のシミュレーションにも使えるのではないか,ひいては小規模であれば,電力系統解析にも応用できるのでは…? そのような思いから,(不十分とは思いますが)デモンストレーションとして,解析モデルを作ってみることにしました。
なお,本記事では公知の回路方式,公知の制御方法をLTspiceのモデルとして実装しただけですので,学術的な新規性は一切ありません💦
三相PWM整流器のモデルの作り方のまとめとして
インターネットを眺めていると,完成したモデルの動作を説明している記事は見掛けるのですが,モデルを組み立てていく過程を紹介しているものは少ないのかと思われます。 三相PWM整流器では,直流電圧制御の内側にマイナーループとして交流電流制御があり,さらに電圧形インバータとしてのPWMがあります。 これらをいっぺんに組み上げてから全体をシミュレーションするというのは,動作確認やデバッグの難易度を考えると,現実的ではないと考えます。 本記事では,下位制御であるPWMからボトムアップでモデルを構築していく過程を記載してみようと思います。
なお,本記事では三相PWM整流器の作り方を記述するのみに留め,PWM整流器の制御上のキモとなる直流電圧制御の詳細については次記事に譲りたいと思います(1つの記事にしてしまうと分量が膨大になりそうなため💦)。
完成したモデルと波形
いきなりですが,どんなモデルと波形が出来上がるのか,イメージを示します。 図1は直流電圧制御,d-q軸上での交流電流制御,PWM,三相PLLを実装したシミュレーションモデル(schematic)です。 また,図2は図1のシミュレーションを実行した波形です。 直流側に電流源負荷を接続し,200 kWの電力を消費しています。 直流電圧を720 V一定に保つため,交流系統から力率1の正弦波電流を取り込むように電流制御しています。 詳細は後述しますが,PLLのおかげで系統電圧の位相,周波数,振幅が急変しても,直流電圧を概ね一定に制御できていることが判りますね。

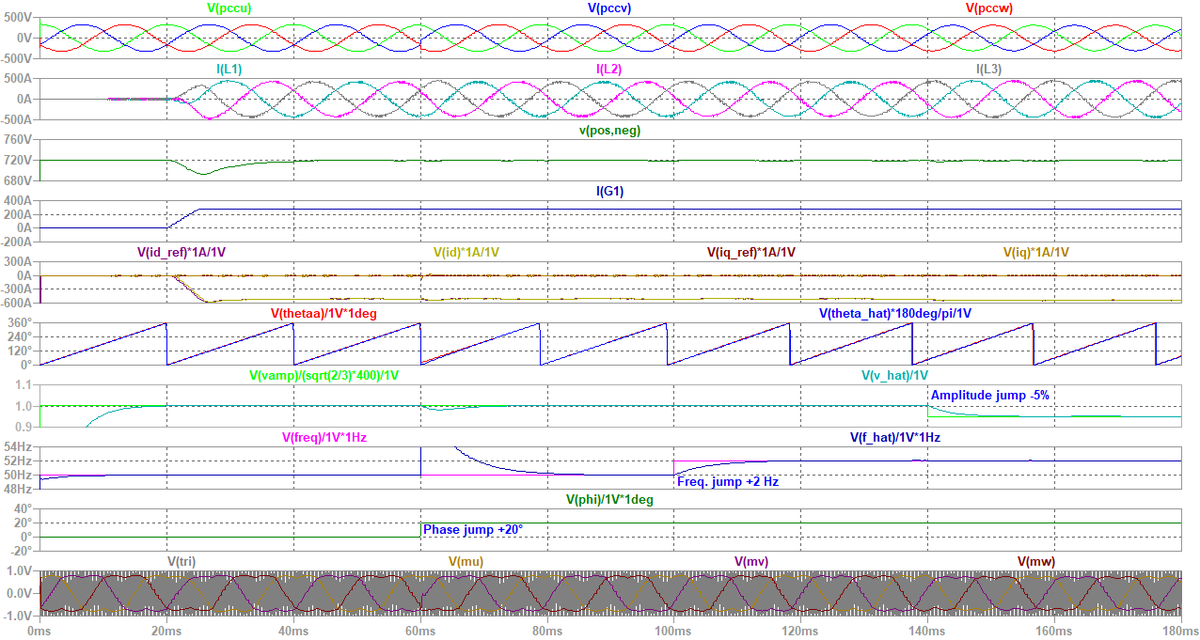
なお,制御系はアナログ制御(連続時間制御)です。 離散時間制御におけるサンプル & ホールドの周波数特性を模擬するため,電圧や電流をセンシングした直後に,移動平均フィルタを置いています。 また,演算によるむだ時間(いわゆる1サンプル遅延)を模擬するため,むだ時間要素を置いています。 これらの考え方は,本ブログの過去の記事にも記載していますので,ご興味のある方はご覧ください*2。
それでは,早速モデル(schematic)を作って行きましょう📝
*1:「系統連系はパワエレじゃない」とのご意見もTwitterで見掛けたことがあります…ちょっと悲しい…です…😥
*2:https://negligible.hatenablog.com/entry/2020/07/15/011258
系統連系インバータの電流制御と系統インピーダンス
はじめに
本ブログでは,電流制御とその安定性に関する記事をいくつか書いて参りました。例えば,下記記事では,サンプル & ホールドと1サンプル遅れを考慮した場合の安定性について,連続時間系に近似した伝達関数に基づく考察を加えてみました。
私のLTspiceのモデルでは単なる電圧制御電圧源(voltage-dependent voltage source, E)を用いて電流を制御しましたが,念頭に置いているのは図1の単線結線図のような系統連系インバータです。ここで,図1のR, Lは連系リアクトルや変換用変圧器など,いわば系統連系インバータ「装置」の内部の既知のインピーダンスです。これまでの本ブログの記事に登場したR, Lと同じと考えて下さい。一方,送配電系統には,その変換器の連系点(PCC, point of common coupling)から上位を見たインピーダンスZsがあり,系統インピーダンスと呼ばれます。なお,図1には他に,Zc,Ze,Zmの3つのインピーダンスを記載しておりますが,これらは後の検討に登場します。

系統インピーダンスがない(Zs = 0 Ω)場合の電流制御系の安定性については,先に挙げた本ブログの記事のように考えることができます。しかし,たとえZs = 0 Ωの条件で安定性を確保できるように電流制御系のゲインを設定していたとしても,系統インピーダンスが存在する(Zs ≠ 0 Ω)場合には,電流制御系が不安定になってしまうことがあります。
まずは例を見てみましょう。


図2は,系統インピーダンスがない(Zs = 0 Ω)場合のステップ応答波形ですが,本ブログの過去の記事*1でご紹介したパラメータK = 1.9の場合です。なお,図3と合わせるため,上から2段目のplot planeは空白としました。
一方,図3は同じK = 1.9の場合ですが,系統インピーダンスが存在することによって不安定となっています。2段目のplot planeにはPCCの電圧をプロットしています。
さて,このような不安定現象が生じるメカニズムとは何でしょうか…?
続きを読むNumWorksのグラフ関数電卓でナイキスト線図を描く
はじめに
フランスのNumWorks社によるグラフ関数電卓(本記事では便宜上,電卓についても「NumWorks」と呼びます)は,比較的低価格,MicroPython搭載,ファームウェアアップデートが頻繁,ハードウェア・ソフトウェアの仕様が公開されている等の特徴を有しており,カシオ,シャープ,キヤノン,HP,Texas Instrumentsなどの既存メーカーの牙城に風穴を開けるべく登場*1した,密かな人気機種となっております。

本記事では,NumWorksがもともと持っている「Functions」アプリを用いて,ナイキスト線図を描く方法をご紹介します。
いきなりですが,こちらがナイキスト線図を描いた結果例です。

あ。点(−1, j0)の左を通っているので,不安定になっていますね💦…なんてことが判ります💫
NumWorksにはオンラインシミュレータがあります。これ自体驚異的です。電卓を実際に購入する前に,いろいろと試すことが可能です。本記事での画像は,基本的にオンラインシミュレータの画面のスクリーンショットです。
続きを読む伝達関数の直接的プロット法と電流制御系
はじめに
線形連続時間時不変システムの入力と出力をラプラス変換(s領域で表現)し,出力と入力の比(=出力÷入力)をとったものを伝達関数と呼びます。 入力が単位インパルス(δ関数)である場合,そのラプラス変換は1ですから, 伝達関数は単位インパルスを入力した場合のシステムの出力そのもの,つまりインパルス応答を表します。
sは複素数です。よくs = σ + jωと書かれます。 当たり前ですが,伝達関数は複素関数となります。 しばしば「複素関数のグラフは描けない」との言葉に出会います。 1変数の実関数y = f(t),例えば
であれば,横軸をt,縦軸をyとすればシンプルにグラフを描けます。

本記事では,伝達関数の直接的プロット法を提案します(これは「新しい」プロット法─と言いたいですが,新しいかどうか判りませんでした💦)。 また,これまでに議論した電流制御系にこのプロット法を適用して,ボード線図やLTspiceによる時間領域でのシミュレーションと比較します。
唐突なアニメーション
いきなりですが,図2のアニメーションをご覧下さい。

これは電流制御系において,制御ゲインを変えながら開ループ・閉ループ伝達関数をプロットしたものを, MatplotlibのFuncAnimationにてGIFアニメとして書き出したものです。
続きを読む続・LTspiceによる電流制御のシミュレーション
はじめに
先日の記事で,LTspiceによる電流制御のシミュレーションについて述べました。 negligible.hatenablog.com
この記事の中で私個人としてひとつの発見と言えるのは,
- 操作量に対してむだ時間T,フィードバック量に対して窓Tの移動平均フィルタを施した連続時間制御システム
- 操作量に対してむだ時間TとPWM,フィードバック量に対してサンプリング周期Tのサンプル & ホールドを設けた離散時間制御システム
がほぼ同じ挙動を示すということです。 図1に上記前者のブロック図を示します。

言い換えれば,離散時間制御 + PWMの電流制御系を,移動平均フィルタとむだ時間のある連続制御系で近似できると言えるのではないでしょうか(PWMの過変調が起きない範囲で)。 例えば図2ですね。

ほぼ挙動は一致しています。 そこで,連続系である図1の安定性について検討してみます。 また,最近はLTspiceばかり触っているので,JupyterLabでボード線図を描いてみました。
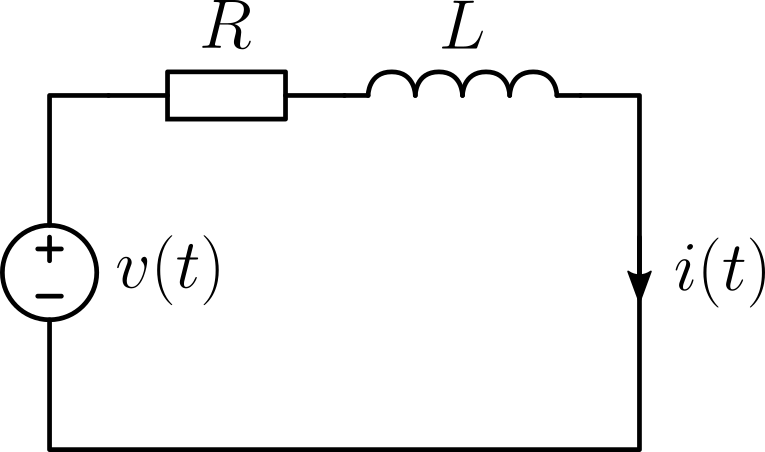
回路定数は先日の記事と同じくR = 20 mΩ,L = 5 mHとします。 また,同じくサンプリング時間 = 移動平均フィルタの窓 = むだ時間T = 100 μsとします。
続きを読むLTspiceのための単相変圧器モデル
はじめに
LTspice XVIIにはいわゆる「変圧器」のモデルが用意されておりません。 2つのインダクタをschematic上に置き,それらの間に結合係数kを設定すると,変圧器として機能させることができます。

さて,LTspiceで変圧器を模擬する方法を解説しているブログ等は多数ありますが, そのいずれもが,「変圧比は,2つのインダクタのインダクタンス比の平方根に等しい」という解説に留まっているように見えます。 例えば図1では,L1 = 4 mH,L2 = 1 mHとしています。 この場合,変圧比は,
となり,2:1の変圧器となります。 結合係数kは大きな値,例えば密結合としてk = 1に設定しておくことができます。 しかし,上記の例…なぜ4 mHと1 mHなのか❓ 36 μHと9 μHではダメなのか❓ 疑問が生じるのではないかと推察します。
続きを読む