NumWorksのグラフ関数電卓でナイキスト線図を描く

はじめに

フランスのNumWorks社によるグラフ関数電卓（本記事では便宜上，電卓についても「NumWorks」と呼びます）は，比較的低価格，MicroPython搭載，ファームウェアアップデートが頻繁，ハードウェア・ソフトウェアの仕様が公開されている等の特徴を有しており，カシオ，シャープ，キヤノン，HP，Texas Instrumentsなどの既存メーカーの牙城に風穴を開けるべく登場*1した，密かな人気機種となっております。

本記事では，NumWorksがもともと持っている「Functions」アプリを用いて，ナイキスト線図を描く方法をご紹介します。

いきなりですが，こちらがナイキスト線図を描いた結果例です。

あ。点(−1, j0)の左を通っているので，不安定になっていますね💦…なんてことが判ります💫

NumWorksにはオンラインシミュレータがあります。これ自体驚異的です。電卓を実際に購入する前に，いろいろと試すことが可能です。本記事での画像は，基本的にオンラインシミュレータの画面のスクリーンショットです。

www.numworks.com

電流制御の開ループ伝達関数

しつこいようですが，従前より本ブログで取り上げているRL回路の電流制御を例として取り扱います。図3に回路図，図4にブロック図を示します。図4は，サンプル & ホールドと1サンプル（演算）遅延がある離散時間（ディジタル）制御システムを，連続時間（アナログ）制御システムで近似したものです。

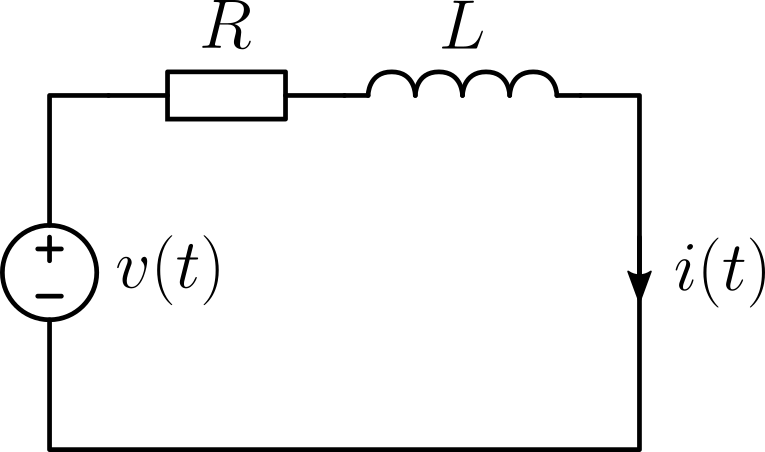
前向き要素をG(s)，フィードバック要素をH(s)とし，開ループ伝達関数をT_o(s)，閉ループ伝達関数をT_c(s)とすれば，

$G(s) = K \left ( K_{P} + \displaystyle \frac{K_{I}}{s} \right ) e^{-s T} \displaystyle \frac{1}{s L + R} \tag{1}$

$H(s) = \displaystyle \frac{1 - e^{-s T}}{s T} \tag{2}$

$T_{o}(s) = G(s) H(s) \tag{3}$

$T_{c}(s) = \displaystyle \frac{G(s)}{1 + G(s) H(s)} \tag{4}$

となります。なお，(1)式のKは図4に現れておりませんが，比例ゲインK_P，積分ゲインK_Iを大きくしたり小さくしたりする係数と考えて下さい。

描きたいのはナイキスト線図なので，(3)式のT_o(s)をプロットすることになります。

また，回路定数等のパラメータはこれまでと同じく表1としました。

パラメータ	値
抵抗器 $R$	$20~\mathrm{m}\Omega$
インダクタ $L$	$5~\mathrm{mH}$
サンプリング周期 $T$	$100~\mu \mathrm{s}$
比例ゲイン $K_{P}$	$\displaystyle \frac{L}{4 T}~[ \mathrm{V/A} ]$
積分ゲイン $K_{I}$	$K_{P} \displaystyle \frac{R}{L}~[ \mathrm{V/As} ]$

過去の記事へのリンクを記載しておきます。

negligible.hatenablog.com negligible.hatenablog.com negligible.hatenablog.com

CalculactionアプリとFunctionsアプリ

NumWorksには，標準で，普通の関数電卓として使えるCalculationアプリ，関数を定義してグラフを描くFunctionsアプリ，MicroPythonでプログラミングが可能なPythonアプリ，確率・統計向けのStatistics，Probability，Regressionの3アプリ，方程式を解くEquationsアプリ，漸化式をプロットするSequencesアプリがあります。

ここで，Pythonアプリは半ば独立しておりますが，例えばCalculationアプリとFunctionsアプリは連携しており，Calculationアプリ内で定義した変数をFunctionsアプリ内で使えたり，逆に，Functionsアプリで定義した関数をCalculationアプリで呼び出したりできます。

また，これは制御工学という観点で重要ですが，NumWorksは複素数を極めてナチュラルに扱えます。国産関数電卓の多くでも複素数を扱えはしますが，大抵は専用の「複素数モード」に入らなければならず，また，そこでは四則演算しかできないという機種が多いのではないでしょうか。しかし，NumWorksでは虚数単位iを含む四則演算以外の計算もこなせます。例えば，

$i^{i} = \left (e^{\frac{\pi}{2} i} \right )^{i} = e^{-\frac{\pi}{2}} \simeq 0.2078796... \tag{5}$

等の計算が可能です*2。

そもそも独立した「i」キーがあります。まぁ，電気工学，制御工学としては虚数単位はjであって欲しいですが，ここは妥協です😅

ナイキスト線図の描き方

それでは，ナイキスト線図の描き方について順を追ってご説明します。

Calculationアプリで変数を設定

Functionsアプリに開ループ伝達関数を入力する際に，各パラメータをリテラル（数値）として入力してしまうと後で例えばインダクタLの値を変更するなどの場合に，制御ゲインの再計算・再入力が必要になり，面倒になってしまいます。言い換えると，定義した伝達関数の再利用性が悪くなります。そこで，FunctionsアプリとCalculationアプリが連携することを利用して，Calculationアプリ内で設定する変数に表1のパラメータを格納し，それをFunctionsアプリで利用することを考えました。

図8: K, K_P, K_Iを設定（ここでは一例としてK = 1.9としています）

数値や式を設定してから[sto→]キーで変数に格納します。そう！数値だけでなく，式も格納できるのは便利です。例えば，図8では，K_IがK_P，R，Lに依存しますが，このようにK_Iを定義しておけば，3つのパラメータいずれかを変更した場合に，K_Iも自動的に更新されます。

開ループ伝達関数の設定

Functionsアプリに入り，開ループ伝達関数T_o(s)を関数f(x)として設定します。

これは仕方がないと思いますが，独立変数は「x」との表記しかできないようです*3。したがって，(3)式の「s」を「x」に置き換えた形で入力します。しかし，その1点以外に関しては，もうそのまま(3)式を入力できてしまいます🎵

あれ？しかし，xことsには

$s = x = j \omega \tag{6}$

として純虚数が入力され，周波数伝達関数f(jω)となって，その値は複素数になるのでは…？どうやってプロットするのでしょうか？

媒介変数表示によるもう1つの関数の定義

そこで，もう1つ関数を定義します。NumWorksのファームウェアVersion 12.2.0（2019年11月12日）より，極座標表示と媒介変数表示の関数もプロットできるようになりました*4。媒介変数表示を活用することでナイキスト線図を描くことができます。要するに，周波数伝達関数f(x) = f(jω)の値を実部と虚部に分けて，それをx，yの値としてしまいます。

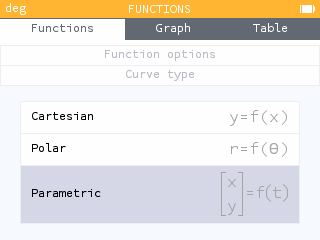
図10のように，もう1つ関数を追加すると，xの関数としてのg(x)，つまりy = g(x)としてグラフを描くような関数が追加されます。媒介変数表示，すなわち[x, y]^T = g(t) = [g_x(t), g_y(t)]の形に変更するため，図11のように設定すると，gはtの関数g(t)となります。デフォルトで，g(t) = [t, 2t]^Tが勝手に入力されているので，これを図12のようにf(x) = f(it)の実部と虚部に設定しましょう。組み込み関数のre()関数とim()関数が使えます。

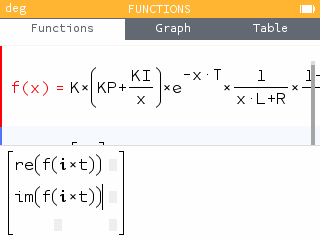
図12: g(t)にf(ix) (=f(jω))の実部と虚部を設定（注：太字のiは虚数単位）

ここでも独立変数の名前は自由に決められず，媒介変数表示の関数では「t」となりますが，要はt = ωです。関数g(t) (= g(ω))を定義する際に，先に定義していたf(x) (= f(s))を利用できる─これもNumWorksの便利なところだと思います。他のグラフ関数電卓 *5でこのような関数の定義はできるでしょうか？ NumWorksのFunctionsアプリでは，「本来の機能は関数の定義であって，グラフ描画は追加の機能である」という思想が貫かれているように思われます。

ナイキスト線図のプロット

ここまでくれば，ナイキスト線図はすぐに描けます。tことωの範囲を設定しましょう。

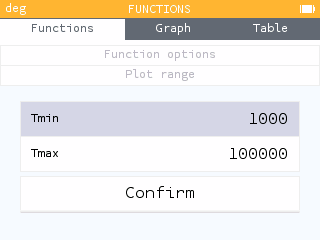
また，グラフに描かないf(x)の方は描画をoffします。

それでは，グラフをプロットします。

なお，図15 ~ 17のようにパラメータKを変えるには，いったんCalculationアプリに戻って，[sto→]キーでKに新しい値を格納して下さい。

なお，デフォルトでは広すぎる範囲が表示されて，肝心の点(−1, j0)の近傍が潰れて見えません。そこで，図18のように，x軸は−3 ~ +3，y軸は−2 ~ +2の範囲を描くように設定しています。

さて，このやり方には残念ながら，位相余裕やゲイン余裕を計算してくれる機能はありません…💧 さらに自由なことがしたければ，MicroPythonでプログラムを作ることが良さそうですね。NumWorksのMicroPythonにも簡易版Matplotlibがあるので，グラフは描けそうです。

まとめ

以上，NumWorks社のグラフ関数電卓によるナイキスト線図の描き方をご説明しました。パソコンでのJupyterLabや，はたまたExcelでもナイキスト線図は描けます。しかし，パソコンが手元にない状況で，安定・不安定を確認しようとした場合に瞬発力を発揮することもあるのではないかと考えております。これ以上の自由度を求めると，前述の通り，MicroPythonで好き勝手にプログラムを作ることが良さそうです。

おまけ1

Matplotlibで，今回NumWorksで描いたものと同じ条件で，ナイキスト線図のアニメーションを作りました🎬 NumWorksではKを手動で設定してグラフを書き直しますが，このアニメーションではK = 0.2 ~ 8.0までを変えながらナイキスト線図を描き，FuncAnimationでアニメ化しています。

おまけ2

前述のNumWorksのオンラインシミュレータですが，画面に表示された電卓の画像上のボタンをマウスでクリックするだけでなく，パソコンのキーボードで直接操作も可能です（パソコンのキーボードでは打てない電卓のキーもあります）。そこで，1つ，罠があります。変数として使えるアルファベットのeとネイピア数eは異なる─という点です。

おわかりいただけただろうか？

そう！ ネイピア数の方はeが少し上を向いています…！こりゃ判りませんて…💦

（追記: 2022-08-03）最新のファームウェア(Version 19)ではネイピア数eと虚数単位iについて専用のフォントを使うことを取りやめ，普通のアルファベットのeとiを使うようになっています。このため，もちろん，eやiに値や式を代入することはできなくなっています。とは言えっても，オンラインシミュレータでパソコンからキーボードで操作するにはこの方が扱いやすいですよね。画面イメージとしては図21をご覧下さい。

www.numworks.com

The characters e and i are now the characters used for the e of the exponential and the complex number i. Indexing of sums and products now uses the variable k.