伝達関数の直接的プロット法と電流制御系

はじめに

線形連続時間時不変システムの入力と出力をラプラス変換（s領域で表現）し，出力と入力の比（＝出力÷入力）をとったものを伝達関数と呼びます。入力が単位インパルス（δ関数）である場合，そのラプラス変換は1ですから，伝達関数は単位インパルスを入力した場合のシステムの出力そのもの，つまりインパルス応答を表します。

sは複素数です。よくs = σ + jωと書かれます。当たり前ですが，伝達関数は複素関数となります。しばしば「複素関数のグラフは描けない」との言葉に出会います。 1変数の実関数y = f(t)，例えば

$y = \sin \omega t \tag{1}$

であれば，横軸をt，縦軸をyとすればシンプルにグラフを描けます。

f:id:s-inoue2010:20200722031538p:plain — 図1: シンプルなy = sin ωtのグラフ（ここではω = 2）

では，F(s)が複素数sの関数だとして，Y = F(s)のグラフは描けるでしょうか？独立変数sにも実部・虚部の2次元があり，得られるY = F(s)にも実部・虚部の2次元があります。せめてYが複素数でなく実数であれば3次元グラフに描けるのですが…こりゃどう描くんだ？

本記事では，伝達関数の直接的プロット法を提案します（これは「新しい」プロット法─と言いたいですが，新しいかどうか判りませんでした💦）。また，これまでに議論した電流制御系にこのプロット法を適用して，ボード線図やLTspiceによる時間領域でのシミュレーションと比較します。

唐突なアニメーション

いきなりですが，図2のアニメーションをご覧下さい。

f:id:s-inoue2010:20200721185319g:plain — 図2: むだ時間要素と移動平均フィルタのある電流制御系の開ループ・閉ループ伝達関数

これは電流制御系において，制御ゲインを変えながら開ループ・閉ループ伝達関数をプロットしたものを， MatplotlibのFuncAnimationにてGIFアニメとして書き出したものです。

これまで，図3のRL回路，図4のブロック図の電流制御系について，2つの記事を書きました。

negligible.hatenablog.com negligible.hatenablog.com

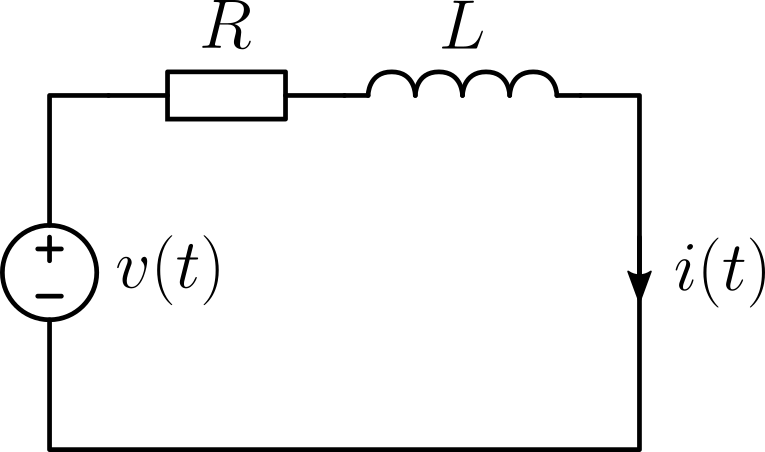
f:id:s-inoue2010:20200702023510p:plain:w250 — 図3: RL回路

f:id:s-inoue2010:20200714180250p:plain:w540 — 図4: 電流制御系のブロック線図（むだ時間と移動平均フィルタあり）

図2は，図4のPI制御器にパラメータKを乗算し，K = 0.2 ~ K = 8までKを変化させた場合のアニメーションです。

伝達関数の直接的プロット法

複素関数である伝達関数をどのように“プロット”するか──そこで，私は伝達関数F(s)があった場合に，

dB表示での絶対値 = 20 log₁₀ |F(s)|，すなわちゲインをコンター図としてプロット
偏角arg F(s)，すなわち位相を流線としてプロット

することを考えました。考えられるs = σ + jωの範囲を絨毯爆撃のように数値的に計算して，無理やりプロットしますので，本記事では直接的プロット法と命名しました。

Matplotlibにおいては，上記1のコンター図をcontour, contourfで描き，上記2の流線はstreamplotで描きます。特に伝達関数の位相を流線で描くというのは，ひょっとしたら新しいアイディアなのではないかと密かに思っています。

電流制御系の伝達関数

前記事の通り，サンプル & ホールド，1サンプル遅れ，PWM (pulse-width modulation)のある離散時間（ディジタル）制御システムを，移動平均フィルタとむだ時間のある連続時間（アナログ）制御システムで近似できます。近似した結果が，前掲の図4となります。

前向き要素をG(s)，フィードバック要素をH(s)とし，開ループ伝達関数をT_o(s)，閉ループ伝達関数をT_c(s)とすれば，

$G(s) = K \left ( K_{P} + \displaystyle \frac{K_{I}}{s} \right ) e^{-s T} \displaystyle \frac{1}{s L + R} \tag{2}$

$H(s) = \displaystyle \frac{1 - e^{-s T}}{s T} \tag{3}$

$T_{o}(s) = G(s) H(s) \tag{4}$

$T_{c}(s) = \displaystyle \frac{G(s)}{1 + G(s) H(s)} \tag{5}$

となります。

計算例

回路定数等のパラメータはこれまでと同じく表1としました。

パラメータ	値
抵抗器 $R$	$20~\mathrm{m}\Omega$
インダクタ $L$	$5~\mathrm{mH}$
サンプリング周期 $T$	$100~\mu \mathrm{s}$
比例ゲイン $K_{P}$	$K \displaystyle \frac{L}{4 T}~[ \mathrm{V/A} ]$
積分ゲイン $K_{I}$	$K_{P} \displaystyle \frac{R}{L}~[ \mathrm{V/As} ]$

K = 0.6の場合

K = 0.6の場合，図5に示すように，閉ループ伝達関数の極は2つの実根となります。また，図6に示すように，開ループ伝達関数のボード線図から位相余裕PM = 77.12°となります。したがって，この場合，システムは安定です。図7に示すLTspiceでの時間領域シミュレーションでは，ステップ応答の時定数が約520 μsであることが分かり，逆数をとれば，1 / 520 μs = 1,923 rad/sと計算できます。図6のボード線図のゲイン交差角周波数と，図4の閉ループ伝達関数の（虚軸に近い方の）極の実部に概ね一致している気がします。

f:id:s-inoue2010:20200722030503p:plain — 図5: K = 0.6の場合の開ループ・閉ループ伝達関数

f:id:s-inoue2010:20200722030545p:plain — 図6: K = 0.6の場合の開ループ伝達関数のボード線図

f:id:s-inoue2010:20200722030620p:plain — 図7: K = 0.6の場合のステップ応答，LTspiceシミュレーション

K = 0.964の場合

K = 0.964の場合，図8に示すように，閉ループ伝達関数の極は重根となっているように見えます。また，図9に示すように，開ループ伝達関数のボード線図から位相余裕PM = 69.34°となります。したがって，この場合，システムは安定です。図10のLTspiceでの時間領域シミュレーションでは，オーバーシュートが発生しておらず，ステップ応答の時定数が約290 μsであることが分かり，逆数をとれば，1 / 290 μs = 3,448 rad/sと計算できます。図9のボード線図のゲイン交差角周波（約2,500 rad/s）とも，図4の閉ループ伝達関数の極とも少しずれている気がしますね。同じく考察が待たれます…。重根だからでしょうか？

f:id:s-inoue2010:20200722033958p:plain — 図8: K = 0.964の場合の開ループ・閉ループ伝達関数

f:id:s-inoue2010:20200722034207p:plain — 図9: K = 0.964の場合の開ループ伝達関数のボード線図

f:id:s-inoue2010:20200722034541p:plain — 図10: K = 0.964の場合のステップ応答，LTspiceシミュレーション

K = 1.9の場合

振動的ではあるが安定限界には至っていないひとつの例として，K = 1.9の場合を考えました。 K = 1.9の場合，図10に示すように，閉ループ伝達関数の極は2つの複素数（共役複素数）となっているように見えます。また，図11に示すように，開ループ伝達関数のボード線図から位相余裕PM = 49.55°となります。したがって，この場合，システムは安定です。図12のLTspiceでの時間領域シミュレーションでは，オーバーシュートが発生しております。オーバーシュートのピークとアンダーシュート*1のピークを半周期と捉えて振動周波数を見積もると，1.2 kHz (= 7,540 rad/s)となります。これは，図10の閉ループ伝達関数の極の虚部と一致しているように見えますね！

f:id:s-inoue2010:20200724003311p:plain — 図10: K = 1.9の場合の開ループ・閉ループ伝達関数

f:id:s-inoue2010:20200724003402p:plain — 図11: K = 1.9の場合の開ループ伝達関数のボード線図

f:id:s-inoue2010:20200724003431p:plain — 図12: K = 1.9の場合のステップ応答，LTspiceシミュレーション

K = 4.39の場合

K = 4.39の場合，図13に示すように，閉ループ伝達関数の極は2つの複素数（共役複素数）となっているように見えますが，ついに虚軸にまで達し，まさに左半平面から右半平面に堕ちて行く安定限界となっています。また，図14に示すように，開ループ伝達関数のボード線図から位相余裕PMはほぼ零(= −0.07°)となっています。図15のLTspiceでの時間領域シミュレーション持続振動が発生しています。振動周波数は1.67 kHz (=10,493 rad/s)であり，やはり，図13の閉ループ伝達関数の極の虚部と一致します。

f:id:s-inoue2010:20200724005751p:plain — 図13: K = 4.39の場合の開ループ・閉ループ伝達関数

f:id:s-inoue2010:20200725011430p:plain — 図14: K = 4.39の場合の開ループ伝達関数のボード線図

f:id:s-inoue2010:20200724010146p:plain — 図15: K = 4.39の場合のステップ応答，LTspiceシミュレーション

移動平均フィルタとむだ時間がなかった場合

図4において，移動平均フィルタとむだ時間がなかった場合，開ループ・閉ループ伝達関数は図16のように描けます。図2と同じく，Kを0.2 ~ 8まで変化させた場合のアニメーションとなります。

f:id:s-inoue2010:20200721185500g:plain — 図16: 理想的な電流制御系の開ループ・閉ループ伝達関数

閉ループ伝達関数の極は実軸上にあるため振動せず，Kを大きくしていくと，ただひたすらに実軸を負の方向に移動していきます。言い換えれば（KI/KP = R/Lとなるように設定し，極零相殺したため）一次遅れ系であり，Kを大きくすると，理論上はいくらでも応答を速くできることが分かります。実際には操作量（制御入力＝電圧）に制約があるため（PWMインバータの直流電圧等），応答速度には限界があります。

しかし，これに移動平均フィルタとむだ時間を追加すると，図2のような複雑な挙動になるというのはなかなかに興味深いですね🎵

あとがき

私は回路と制御の世界で生きてきたので，2次元や3次元に分布する物理量を描くコンター図に少し憧れていました😅 いました？いや，今でもOpenFOAMのような3次元CAEツールを使いこなす人には憧れを抱きますね🤩

今回は，水戸にある妻の実家から記事を投稿しました。子どもたちはじいじ・ばあばと一緒に遊べて大変楽しいようです🤣 明日は天気が好転すると良いのですが…。

【追記】K = 1.9の場合の閉ループ伝達関数の極の実部について

極の実部にも言及しておくべきでしたね😅 図10に見える2つの極（複素共役）を

$s_{p} = \sigma_{p} \pm j \omega_{p} \tag{6}$

とすると，閉ループ伝達関数の分母多項式は，次式を因数として含みます。

$\{s - (\sigma_{p} + j \omega_{n}) \} \{s - (\sigma_{p} - j \omega_{n}) \} = s^{2} - 2 \sigma_{p} s + \sigma_{p}^{2} + \omega_{p}^{2} \tag{7}$

これを，2次遅れ系の標準的な分母多項式

$s^{2} + 2 \zeta \omega_{n} s + \omega_{n}^{2} \tag{8}$

と比較すれば，

$\sigma_{p} = - \zeta \omega_{n} \tag{9}$

$\sigma_{p}^{2} + \omega_{p}^{2} = \omega_{n}^{2} \tag{10}$

を満足するはずです。 (9)，(10)式をζ，ω_nについて解けば，

$\zeta = \displaystyle - \frac{\sigma_{p}}{2 \sqrt{\sigma_{p}^{2} + \omega_{p}^{2}}} \tag{11}$

$\omega_{n} = \sqrt{\sigma_{p}^{2} + \omega_{p}^{2}} \tag{12}$

を得ます。逆に，(9)，(10)式をσ_p，ω_pについて解けば，

$\sigma_{p} = - \zeta \omega_{n} \tag{13}$

$\omega_{p} = \omega_{n} \sqrt{1 - \zeta^{2}} \tag{14}$

を得ます（注：(13)式は(9)式とまるっきり同じです。最初からσ_pは解けています💦）。

図10において，s_p = −4,000 ± j7,500と読み取れば，

$\zeta = -\displaystyle \frac{-4,000}{\sqrt{(-4,000)^{2} + 7,500^{2}}} \simeq 0.4706 \tag{15}$

$\omega_{n} = \displaystyle \sqrt{(-4,000)^{2} + 7,500^{2}} \simeq 8,500~\mathrm{rad/s} \tag{16}$

と計算できます。特に減衰係数ζは正しいのでしょうか？ LTspiceでω_n = 1，ζ = 0.4706の場合の2次遅れ系のステップ応答をシミュレーションしてみると──。

f:id:s-inoue2010:20200727012127p:plain — 図16: ω_n = 1, ζ = 0.4706の場合のLTspiceによるステップ応答シミュレーション

オーバーシュートが1.2に近いことや，振動の様相などが図12の波形に近いことが分かります。ただし立ち上がりの波形が若干異なりますね。図12は直線的に立ち上がっていますが，図16は2次系らしく弧を描いていますね。図10の範囲外にまだ極や零点があるのかな…？

オーバーシュートのピークからアンダーシュートのピークの間の時間は，（LTspiceのカーソルで読み取れば）図示の通り3.542 sでした。これは半周期なので1周期では倍の7.084 s，その逆数は0.1412 Hzとなって，2πを掛けて角周波数とすれば0.887 rad/sとなります。これが前述のω_pに該当するはずです。実際，計算してみると，

$\omega_{p} = \omega_{n} \sqrt{1 - \zeta^{2}} = 1 \times \sqrt{1 - 0.4706^{2}} = 0.882~\mathrm{rad/s} \tag{17}$