はじめに
前記事から間が開いてしまいました。もう秋に入りつつありますが,まだまだ暑い日が続いていますね。 本記事では,LTspiceで三相PWM整流器(回生もできるので,一般の三相系統連系変換器*1として考えてください)を作った過程を書いてみました。
自作制御ライブラリの活用例として
さて,前記事を書き終えた後,LTspice向けに開発中の自作制御ライブラリContrailleの活用例の1つとして,三相PWM整流器を作ることにしました。 LTspiceというと,「オペアンプ等のアナログ回路やスイッチング電源のシミュレーションに使うもの」というイメージがありますが,系統連系変換器のシミュレーションにも使えるのではないか,ひいては小規模であれば,電力系統解析にも応用できるのでは…? そのような思いから,(不十分とは思いますが)デモンストレーションとして,解析モデルを作ってみることにしました。
なお,本記事では公知の回路方式,公知の制御方法をLTspiceのモデルとして実装しただけですので,学術的な新規性は一切ありません💦
三相PWM整流器のモデルの作り方のまとめとして
インターネットを眺めていると,完成したモデルの動作を説明している記事は見掛けるのですが,モデルを組み立てていく過程を紹介しているものは少ないのかと思われます。 三相PWM整流器では,直流電圧制御の内側にマイナーループとして交流電流制御があり,さらに電圧形インバータとしてのPWMがあります。 これらをいっぺんに組み上げてから全体をシミュレーションするというのは,動作確認やデバッグの難易度を考えると,現実的ではないと考えます。 本記事では,下位制御であるPWMからボトムアップでモデルを構築していく過程を記載してみようと思います。
なお,本記事では三相PWM整流器の作り方を記述するのみに留め,PWM整流器の制御上のキモとなる直流電圧制御の詳細については次記事に譲りたいと思います(1つの記事にしてしまうと分量が膨大になりそうなため💦)。
完成したモデルと波形
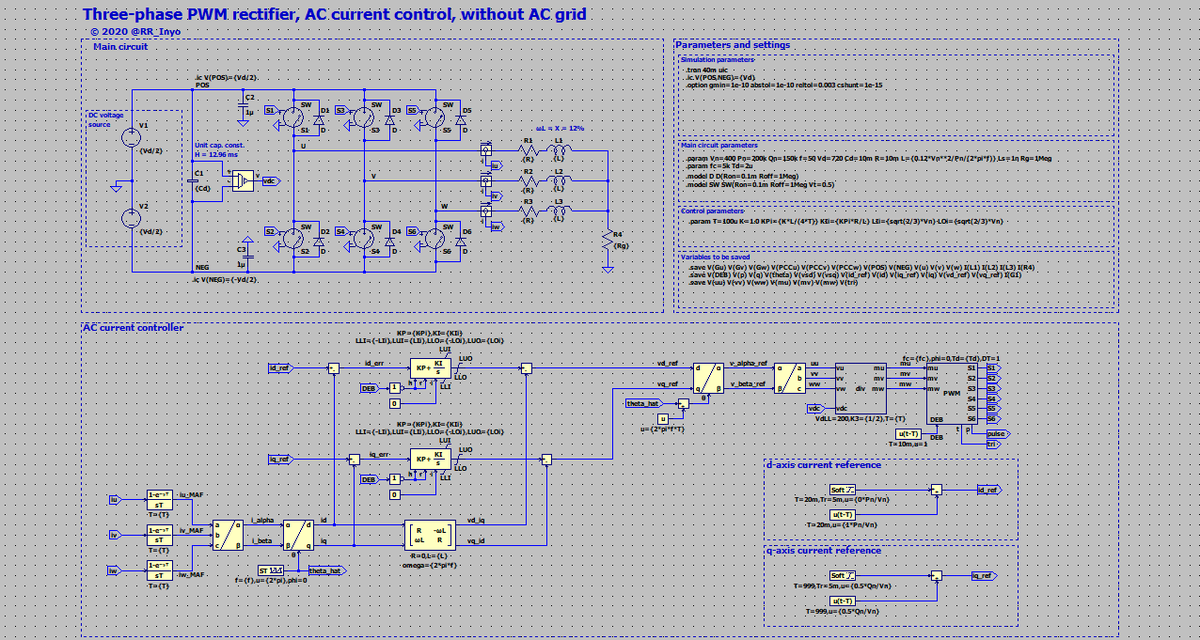
いきなりですが,どんなモデルと波形が出来上がるのか,イメージを示します。 図1は直流電圧制御,d-q軸上での交流電流制御,PWM,三相PLLを実装したシミュレーションモデル(schematic)です。 また,図2は図1のシミュレーションを実行した波形です。 直流側に電流源負荷を接続し,200 kWの電力を消費しています。 直流電圧を720 V一定に保つため,交流系統から力率1の正弦波電流を取り込むように電流制御しています。 詳細は後述しますが,PLLのおかげで系統電圧の位相,周波数,振幅が急変しても,直流電圧を概ね一定に制御できていることが判りますね。

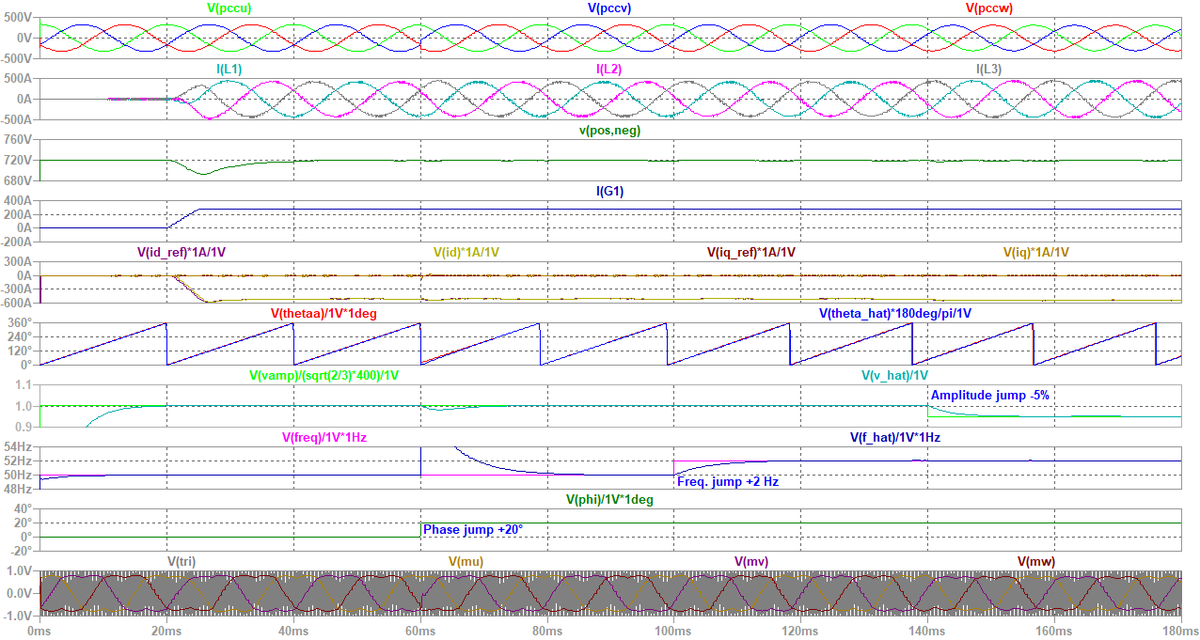
なお,制御系はアナログ制御(連続時間制御)です。 離散時間制御におけるサンプル & ホールドの周波数特性を模擬するため,電圧や電流をセンシングした直後に,移動平均フィルタを置いています。 また,演算によるむだ時間(いわゆる1サンプル遅延)を模擬するため,むだ時間要素を置いています。 これらの考え方は,本ブログの過去の記事にも記載していますので,ご興味のある方はご覧ください*2。
それでは,早速モデル(schematic)を作って行きましょう📝
本記事で考える三相PWM整流器
概略仕様
まずは,どのような整流器を作るかを考えなくてはなりません。 今回モデル化する三相PWM整流器としては,三相400 V,50 Hzの交流系統に(トランスレスで)連系する,定格有効電力±200 kW*3,定格無効電力±150 kvarのものを想定しました。 小規模な太陽光発電PCSのようなイメージです*4。 主回路方式は最も単純な三相2レベル電圧形インバータとします。
交流系統の電圧や周波数も変動しますので,これも考慮に入れる必要があります。 ここでは,系統電圧0.95 p.u. ~ 1.05 p.u.,周波数48 Hz ~ 52 Hzの範囲で,±200 kW,±150 kvarの有効・無効電力を維持できることを考えます。 また,スイッチング周波数(三角波キャリア周波数)を5 kHz,連系リアクタンスを12%(400 V,200 kWベース),その巻線抵抗を10 mΩとします。
さらに,系統電圧1 p.u.で有効・無効電力がともに零である場合(後述の図4における運転点0)の変調率が0.8程度であり,キリがいい数として,仮に直流電圧を720 Vとします。 この条件でPWMの変調率の変動範囲を計算し,過変調にならないことを確認します。
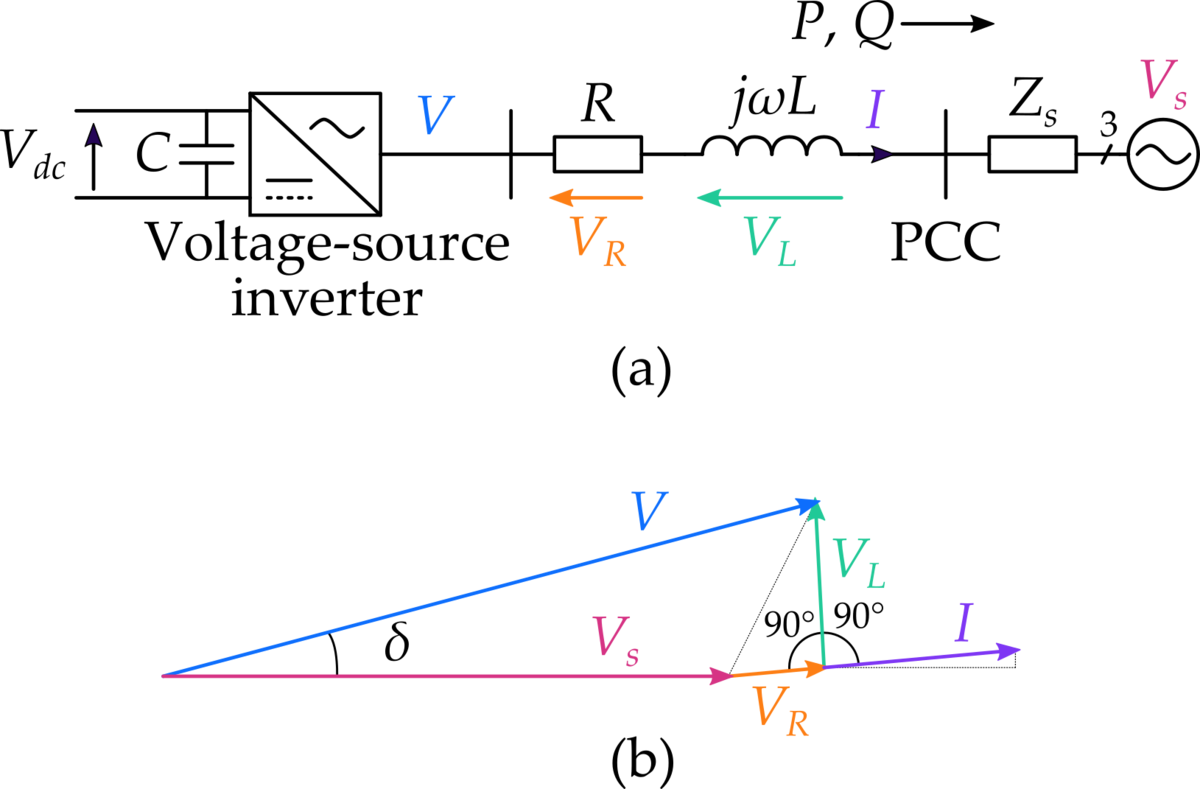
図3に,三相PWM整流器の概略単線結線図とフェーザ図を示します。 とりあえず,PWMによるスイッチングリプルは無視しています*5。 また,図3(b)のフェーザ図では,同図(a)の系統インピーダンスZsを無視(Zs = 0)しています。
本記事では,図3(a)の「voltage-source inverter」を「インバータ」と呼び,インバータ,R,jωLの組を「三相PWM整流器」,「PWM整流器」,または単に「整流器」と呼ぶことにします。
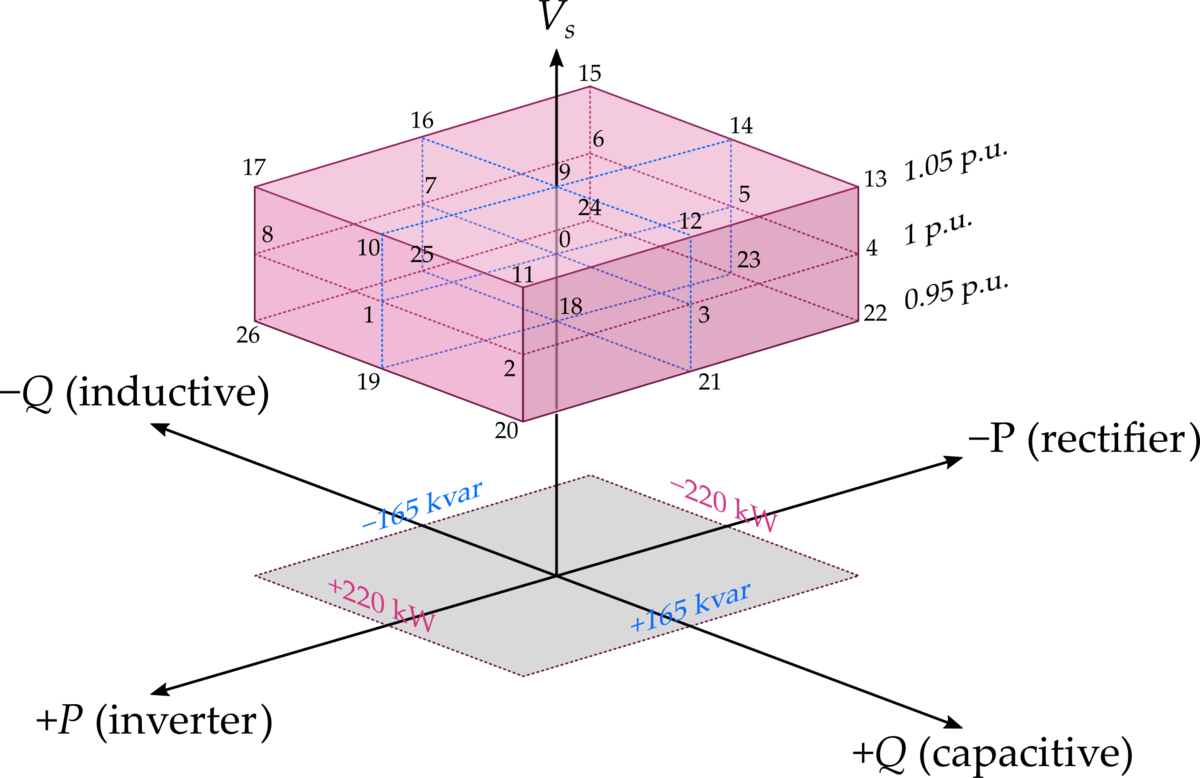
有効電力P,無効電力Q,系統電圧Vsの運転可能であるべき範囲を3次元的に描くと,図4となります。 ここでは,PとQにそれぞれ10%のマージンを持たせ,±220 kW,±165 kvarとしています。 また,代表的な運転点に0 ~ 26の番号を付けています。 なお,図4には周波数を表現できていません。1つの運転点でも48 ~ 52 Hzの周波数範囲があります。
Excelによる主回路定数の確認
図3(b)のフェーザ図において,周波数fを48 Hz,50 Hz,52 Hzの3パターンに変化させながら,図4の各運転点(P, Q, Vs)における交流電流やPWMの変調率を計算しました。 この計算には最強のエンジニアリングツール(?)の1つ,Microsoft Excelを用いました📊 一般にあまり知られていないかもしれませんが,Excelは複素数を扱うことができるので*6,電気回路のフェーザの計算に非常に役に立ちます。 PythonではExcel以上にネイティブに複素数に対応していますが,このような場合はPythonでプログラムを組むより,Excelで計算した方が人間の作業量は少ないのではと思っています。
結果,図5を得ました。
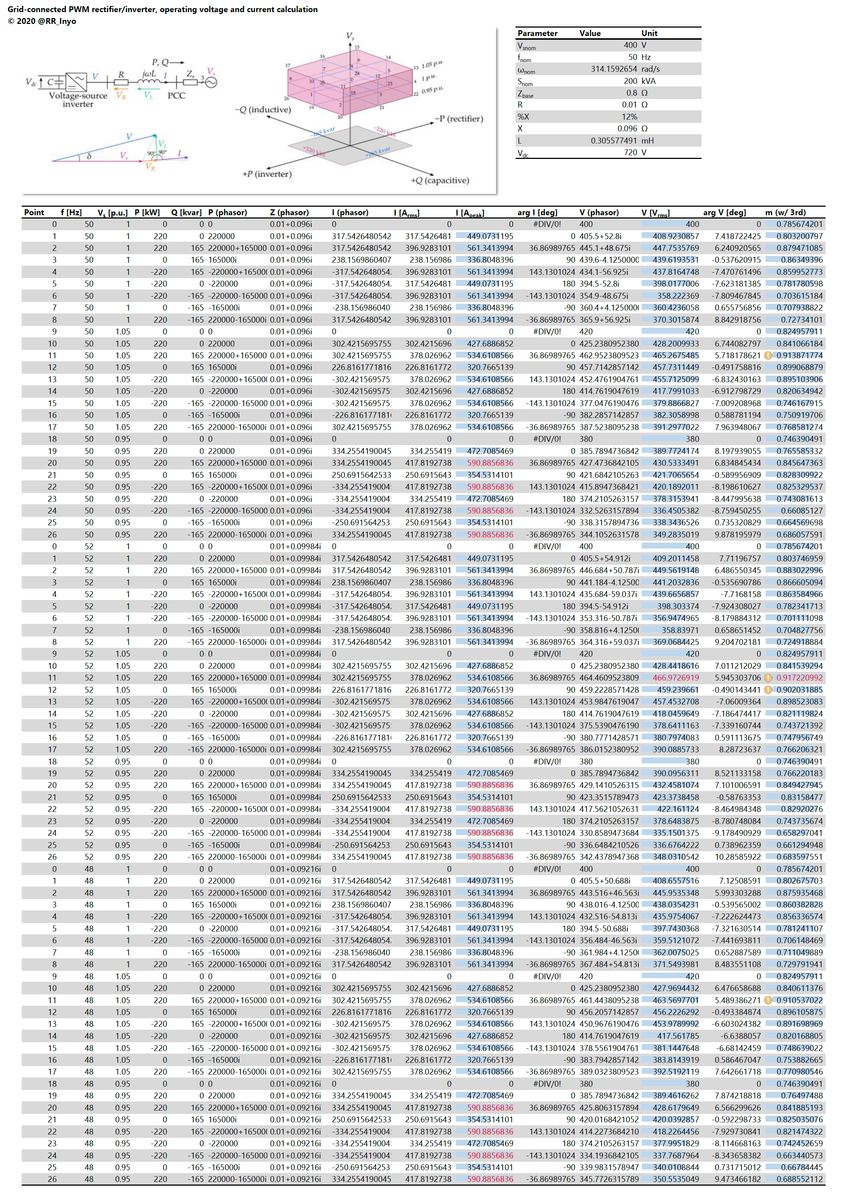
交流電流が最大となるのは周波数に関わらず運転点20,22,24,26の場合でそのピーク値は591 Aとなります。 これは,系統電圧が0.95 p.u. (380 V)であるときに,P = ±220 kW,Q = ±165 kvarを出力する場合に相当します。 系統電圧が低下したため,同じ電力を授受するには電流を大きくする必要があるためですね。
また,PWMの変調率が最大となるのは,周波数f = 52 Hzの場合の運転点11です。最大変調率は0.917となりました*7。 系統電圧が1.05 p.u.に上昇している状態で,周波数fも52 Hzに上昇し,連系リアクトルのリアクタンスが大きく見える中で,P = +220 kW(インバータ),Q = +165 kvar(容量性)を出力している状態ですね*8。 また,インバータ運転である運転点11と整流器運転である運転点13を比較すると,連系インピーダンスの抵抗成分R = 10 mΩの電圧降下がそれぞれ上乗せされるか差し引かれるかという差が生じますので,運転点11の方が高い変調率となります(運転点11では0.917ですが運転点13では0.914に留まります)。
直流コンデンサは仮でC = 10 mFとしました。 定格有効電力200 kW,定格直流電圧720 Vから単位静電定数Hを計算すると,H = 12.96 msとなります。
以上をまとめると,表1となります。
| パラメータ | 値 |
|---|---|
| 主回路方式 | 三相2レベル電圧形インバータ |
| 定格系統電圧 | 400 V |
| 系統電圧変動範囲 | 0.95 p.u. (380 V) ~ 1.05 p.u. (420 V) |
| 定格周波数 | 50 Hz |
| 周波数変動範囲 | 48 ~ 52 Hz |
| 定格有効電力 | ±200 kW |
| 定格無効電力 | ±150 kvar |
| 定格直流電圧 | 720 V |
| 連系リアクトルL | 12% (L = 306 μH) |
| 連系リアクトルの巻線抵抗R | 10 mΩ |
| 直流コンデンサC | 10 mF (H = 12.96 ms) |
モデル作成の基本的な考え方
本記事の例に限らず,一般に何らかのシステムのシミュレーションモデルを作る際,
- システム全体を考えたマクロの動きを模擬してから,徐々に下位のサブシステムのミクロな動きを作り込んでいく(トップダウン)
- ミクロな動きを再現する各サブシステムの動きを確認しながら,徐々にマクロ,つまりシステム全体を組み上げていく(ボトムアップ)
という2つの考え方があると思います。 本記事では後者のボトムアップの方法で三相PWM整流器を組んでいきます。
三相PWM整流器においては,最上位に直流電圧制御系がありますが,直流電圧vdcを一定に制御するには交流電流iを自在に制御する必要があります。 言い換えれば,直流電圧制御の下位に交流電流制御があります。 これは,モータ制御において,速度を制御するために,トルクを制御しなければならないことに似ていますね。 フィードバック制御としてのフィードバックループを考えた場合,外側の直流電圧制御のフィードバックループの内側に,電流制御のフィードバックループが入れ子になっているため,電流マイナーループと称することが多いですね。
さて,交流電流iを制御するためには,インバータの出力電圧vを制御する必要がありますね。 これもまた,指令値通りの電圧を出力できているか,指令値と実際の値を比較するフィードバック制御をする必要があり……いや,その必要はありません。 電圧形インバータなので,適切なパルスさえ作れば,思った通りの電圧を出力できると考えます*9。 本記事では,指令値通りの電圧を生み出すパルスを作る方法として,最も一般的な三角波比較PWMを実装することにします。以降では三角波比較PWMを単に「PWM」と呼ぶことにします。
以上をまとめると,最下層の制御はPWMであり,その上に交流電流制御,さらにその上に直流電圧制御が乗っかる形になります。
もう1つ,PWM整流器をはじめとする系統連系変換器では,交流系統の電圧位相を知る必要があります。 交流系統の電圧位相が判らなければ,系統から有効電力を取り込みたい場合に,どの位相で交流電流を流すように制御すれば良いか分かりません。 そこで,交流系統の電圧位相を検出するPLL (phase-locked loop)が必要です。
本記事では,
- PWM
- 三相電圧形インバータ主回路
- d-q座標系での三相交流電流制御(交流系統なし)
- 交流系統への連系
- 直流電圧制御の追加
- 三相PLLの追加
の順で1つずつ組み上げていくこととします。
PWMを作る
1レグPWM
三相2レベル電圧形インバータにはレグが3つあり,それぞれのレグに上下2つ,合計6つのアーム(オン・オフ制御電力用半導体デバイス(IGBT等)と環流ダイオードの組)があります。 したがって,PWMのための制御ブロックも6つ必要です。 まずは1レグのためのPWMを作ってみましょう。
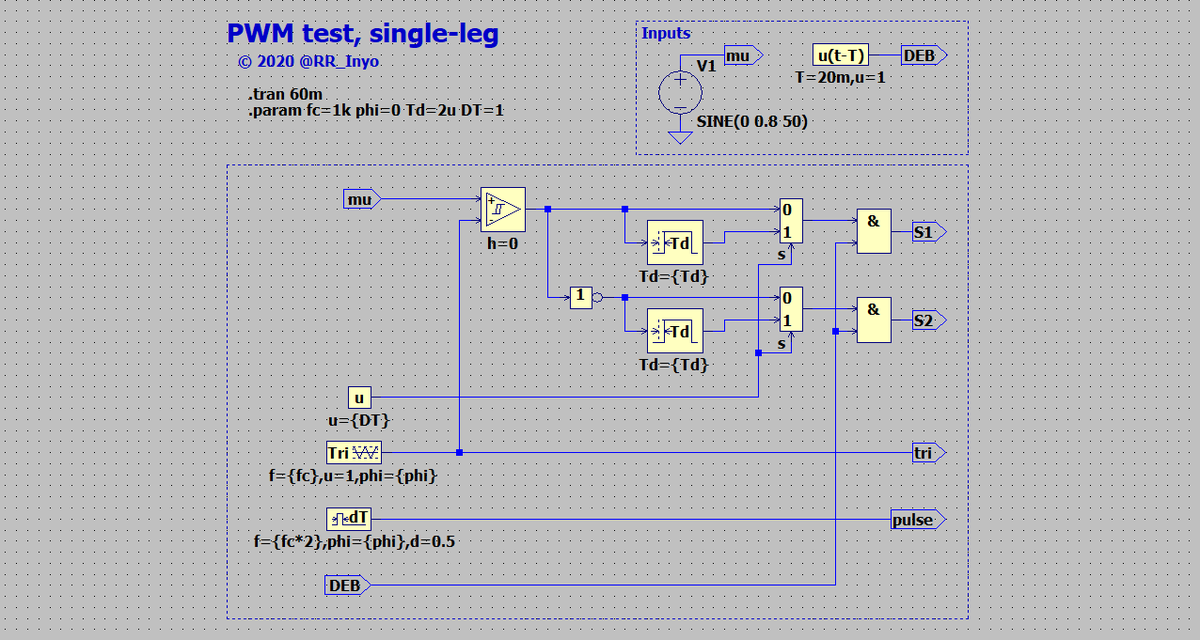
図6に1レグPWMの制御ブロックを示します*10。変調波muを振幅1の三角波triと比較した結果と,それをNOTゲートで反転したもの,合計2つの出力を得ます。それぞれ上アームと下アームのゲートパルスとします。 オンディレイTdによるデッドタイムを設けた出力か,デッドタイムを設けないそのままの出力を用いるか,マルチプレクサで選択できるようにしています。最後に,それぞれのゲートパルスとDEB信号をANDゲートに入力し,DEB = 0の場合*11には結果であるS1とS2は常時S1 = S2 = 0となる,つまり,常時オフさせる信号が出力され,DEB = 1となった場合に変調波muと三角波との比較で決まるゲートパルスをS1,S2に出力します。 DEBは「deblock」の略です。
もう1つの出力信号pulseは,本記事では使いませんが,三角波キャリアtriのピークとボトムと同期した矩形波を出力します。 これは,三角波のピークとボトムで電圧や電流をサンプリングする離散時間制御(ディジタル制御)システムを作る際のクロック信号となります。 ここでは,三角波キャリアのスイッチング周波数は,動作を分かり易くするため1 kHzとしています。
右上に,このブロックの動作確認のための入力信号を作りました(四角形で囲まれたInputsの部分)。 本来,このブロックは(ボトムアップで作っているため),より上位の回路での階層化ブロック(hierarchical block)となって,変調波mu等の入力信号は外部から与えられる*12のですが,階層化ブロック単体でテストするには,何か信号源が必要となります。
余談ですが,Pythonではモジュールを作る際に
if __name__ == '__main__':
というif文で,他のモジュールから呼ばれておらず,自モジュール単体で動いていることを判別して,例えば単体で動いている場合にはテスト用の入力を作ったりできます。 同様の仕組みがLTspiceにもあれば,図6の右上の「Inputs」の扱いがラクになるのになぁ─と思ったりしています。 今回の場合は階層化ブロックとする前に,右上の「Inputs」は削除します。
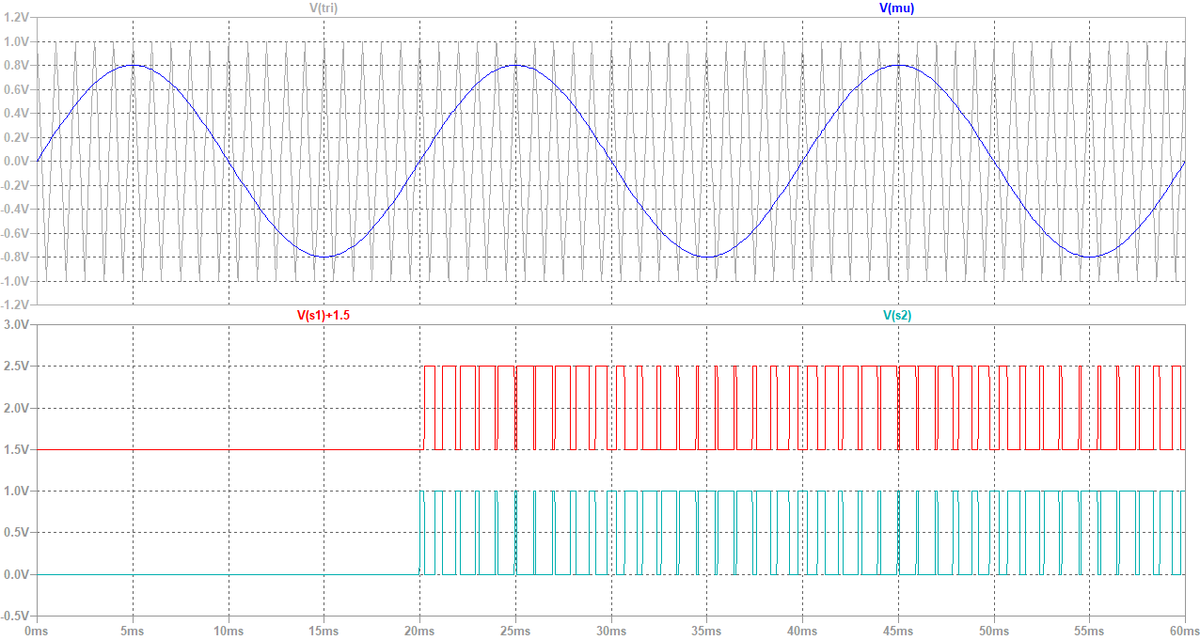
図6をシミュレーションすると,図7の波形が得られます。 図示していませんが,時刻t = 20 msでDEB信号が立ち上がるとS1,S2にPWMによるゲート信号が現れ始めます。
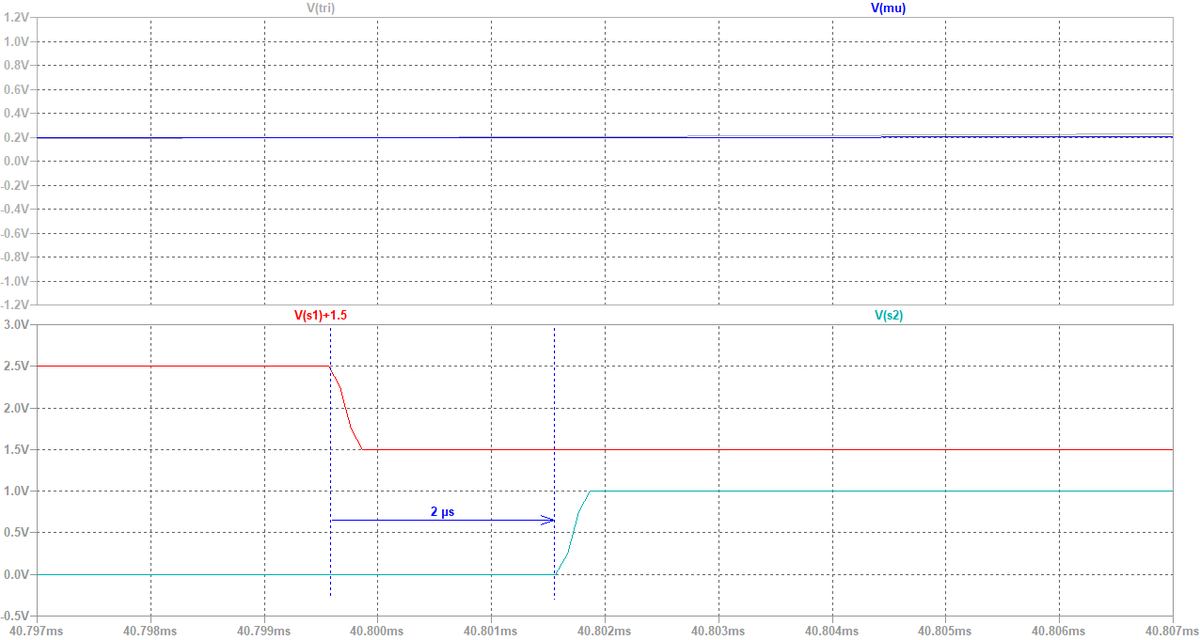
図8は図7の拡大波形です。 ここではデッドタイムTdを2 μsに設定しましたが,その通り,2 μsのデッドタイムを確保できていることが判ります。
三相PWM
三相PWMではレグが3つとなるため,図6のパルス生成部分をコピー & ペーストすることで簡単に作ることができます。 図9に三相PWMのブロック図を示します*13。
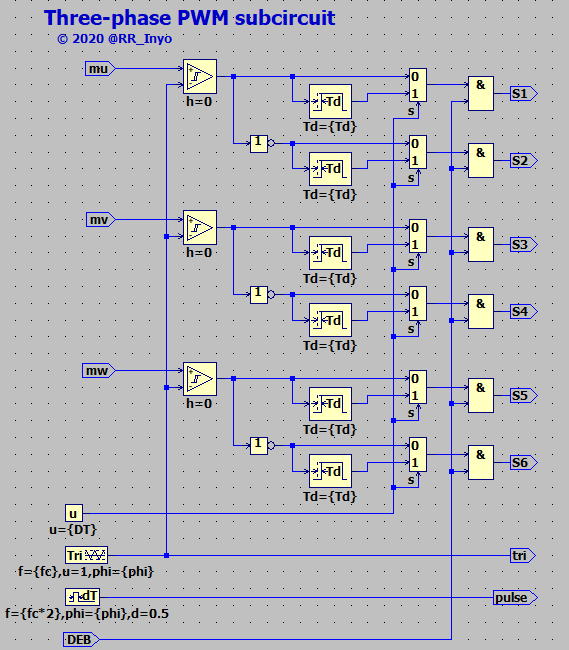
さらに,図10にシミュレーション波形を示します。 図7と比較すると,単純に入出力の信号数が増加したのみで,本質は変わっていないことが判ります。
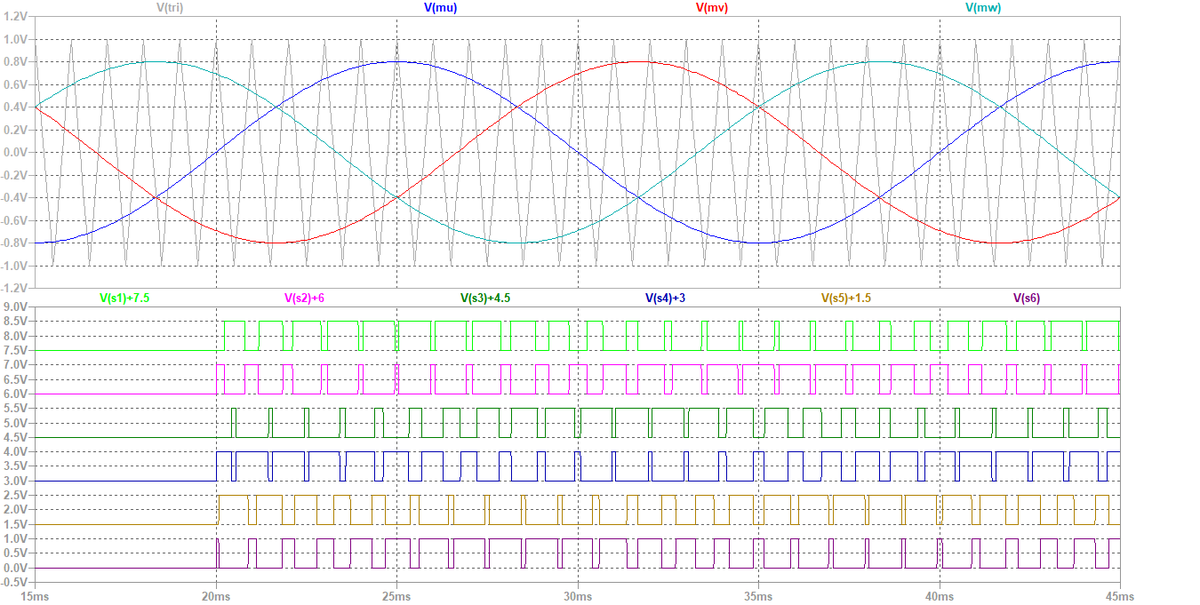
以上で,PWMを作ることができました。
三相2レベル電圧形PWMインバータを作る
次はインバータの主回路です。 せっかくのLTspiceなので,各半導体メーカーが提供しているIGBT等のSPICEモデルを使うこともできるとは思いますが,今回は制御系で遊ぶことが目的なので,本記事では電力用半導体デバイスを理想素子として実装することにします*14。
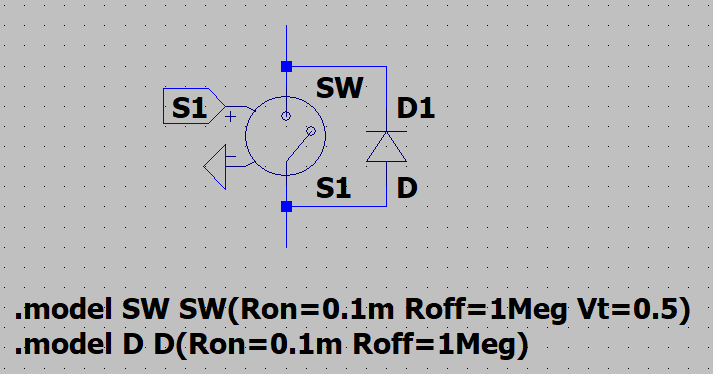
具体的には,図11に示すように,LTspiceに標準で用意されている電圧制御スイッチとダイオードを用います。 スイッチはデフォルトのオン抵抗Ronが1 Ωなのでこれを0.1 mΩに設定します。 またデフォルトのスレショールド電圧Vtが0 Vなので,0 Vをオフ,1 Vをオンとするようなゲートパルスではうまく制御できないことがあります*15。対策としてVtを0.5 Vに設定し直しています。 ダイオードに関しては,同じくデフォルトのオン抵抗Ronが1 Ωなのでこれを0.1 mΩに設定し,また,オフ抵抗Roffを1 MΩに設定しています(デフォルトでは1 / Gminなので,大きすぎて計算が発散する恐れがあります)。
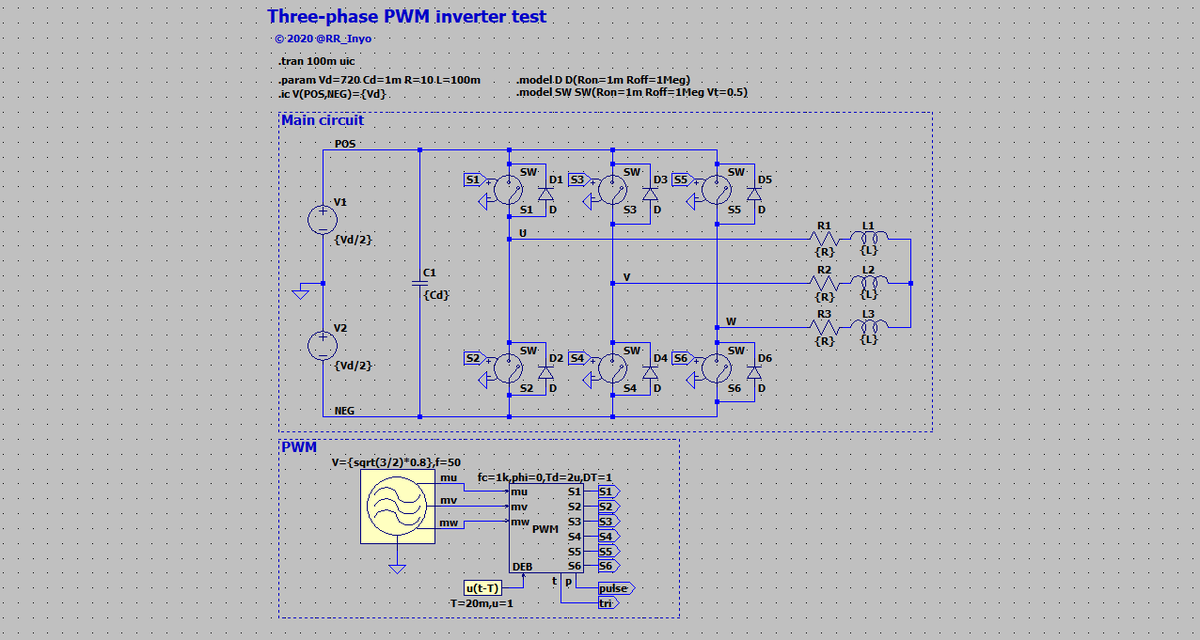
図12に,組みあがった三相2レベル電圧形PWMインバータを示します。 また,前節で作成した三相PWMを階層化ブロックとして組み込み,三相の信号源を変調波として与えています。 信号源の振幅を0.8 V,すなわち変調率0.8とします*16。 変調波の周波数は50 Hzです。
インバータの直流側には360 Vの直流電圧源を2つ直列接続し,中点をGNDとしました。 なお,1 mFの直流コンデンサを設けていますが,直流電圧源と並列接続されているため,回路の動作上,意味はありません(後で接続する場所に困らないよう,スペースを確保する目的で置きました)。 また,交流側には10 Ωの抵抗器と100 mHのインダクタを(適当に💦)接続しました。 前節と同じく,三角波キャリアのスイッチング周波数は,動作を分かり易くするため1 kHzとしています。
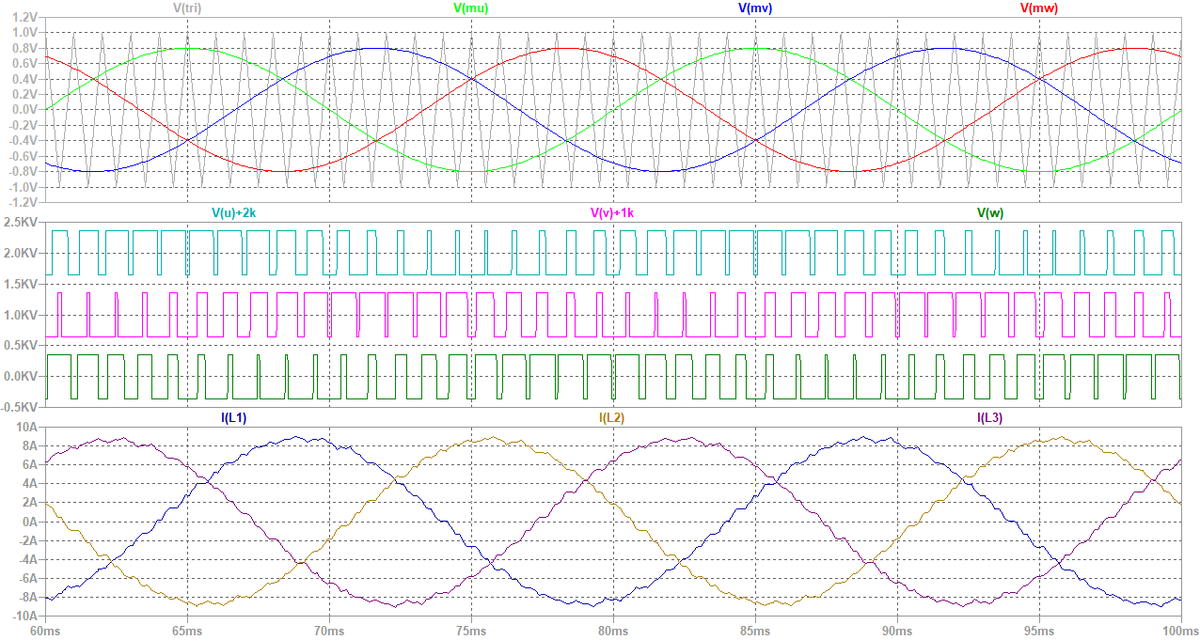
図13にシミュレーション波形を示します。 直流電圧720 V,変調率0.8なので,出力相電圧の振幅Voは
となります。 一方,基本波50 Hzにおける負荷インピーダンスZLの絶対値|ZL|は,
となります。したがって,基本波成分のみに着目すれば,電流振幅Iは,
となります。図13における電流振幅は約9 Aと読み取れ,概ね一致していることが判ります。
以上で,インバータを作ることができました。
d-q座標系での三相交流電流制御を作る
座標変換の概要
まず,座標変換に関しては,下記リンクに示すMathWorksさんの解説が極めて分かり易いので,これをご参照下さい。
三相交流と言っても,三相3線の場合は電流の和が零になるという制約があるため,電流の自由度は2となります。 そこで,三相交流電流を二相交流電流に「座標変換」して制御しようというアイディアが生まれました。 これを,三相-二相変換,α-β変換,Clarke変換等と呼びます*17。 好みの問題とは思いますが,本記事ではこれを「α-β変換」と呼ぶことにします。 三相平衡であれば,電流の位相は120°ずつシフトします。 これをα-β変換すると,位相が90°シフトした2つの電流に変換されます。 α成分を横軸,β成分を縦軸に取ると(これをα-β座標系と呼びます),電流の軌跡は1周期で1周して円を描きます。
余談ですが,α-β座標系に電流(や電圧)をプロットする際に,原点からの矢印(ベクトル)として描く場合が,教科書やインターネット上の解説ではほとんどです(上記のMathWorksさんのページもそうですね)。 しかし,私個人としては,この描き方は必ずしも本質を表していないのではと考えています。 どちらかと言うと,矢印の先端の点だけが重要なので,ある瞬間の電流がα-β座標系における1点として表現できることが重要かと理解しています。
さて,α-β変換ではまだ交流です。 交流電流を交流のままフィードバック制御しようとすると,交流的に変動する指令値に常に追従するようなサーボ系としなければならず,制御系の設計が難しくなります。 そこで,α-β座標系の上で回転する電流と同じ角速度で回転するd-q座標系を作り, d-q座標系の上では電流が止まって見える*18,つまり,直流に見えるように座標変換してから制御する方法が考案されました。 これをd-q変換またはPark変換と呼びます*19。本記事ではこれを「d-q変換」と呼ぶことにします。 直流に変換されているので,定値制御,プロセス系として考えることができ,積分制御によって容易に定常偏差を零にできます。
三相PWM整流器をはじめとする三相系統連系変換器では,三相交流電流をα-β変換,d-q変換した上で制御することが一般に行われております。 本記事でも,α-β変換,d-q変換を実装します。
d-q座標系での等価回路
図14に2つの三相電圧源がRとLを介して向き合っている三相回路とそのd軸・q軸等価回路を示します。 この2つの三相電圧源ですが,もちろんvu, v, wは系統連系インバータを,vsu, sv, swは交流系統を表しています。

さて,図14(a)では次式が成立しますね。
(4)式は実は図3(b)のフェーザ図と同じことを言っています。 詳細は次記事にて書くつもりですが,(4)式にα-β変換,d-q変換を施します。 すると,(4)式はd-q座標系において,次式のように書き表すことができます。
さらに,
として,時間微分演算子pを行列に入れ込み,かつ,Rも行列に入れ込む形で整理すると,
と書けます。図14(b),(c)は(7)式を回路図として表現したものになります。 d軸等価回路とq軸等価回路には相互干渉((7)式の2 × 2行列中の− ω Lとω Lを干渉項と呼びます)がありますが, これさえきちんと管理(=フィードフォワード制御で打ち消す)すれば,d軸とq軸の電流id,iqを独立に制御できます。
また,(5)式から電流[id, iq]Tに関する状態方程式として表現すると,
と書けますね*20。
慣習的に,系統連系変換器ではd軸を交流系統のu相の(cosとしての)電圧位相に合わせます。 こうすると,idとiqはそれぞれ有効電流と無効電流となります。 モータ制御の場合と,d軸,q軸のイメージが異なるので注意が必要です。
図14(b),(c)にて干渉項がないと考えれば,それぞれの回路は,本ブログの過去の記事に記載の電流制御と同様に考えることができます。
d-q座標系での電流制御を設けたモデル
まずは,図14における系統電圧vsu, sv, swがない場合の電流制御を作ります。 図15に出来上がったschematicを示します。 電流iu,iv,iwを検出してα-β変換とd-q変換を施し, d-q座標系で指令値id_refとiq_refと比較してそれぞれ比例積分(proportional-integral, PI)制御しています。 得られたd-q座標系での電圧指令値vd_refとvq_refを逆d-q変換,逆α-β変換して三相の電圧指令値を得て,さらにこれをPWMの変調波mu,mv,mwに換算します。
ここで,図15の直流側には図12と同じく,直流電圧源を接続しています。 そう! まだまだPWM整流器にはなってませんので,ご注意下さい。
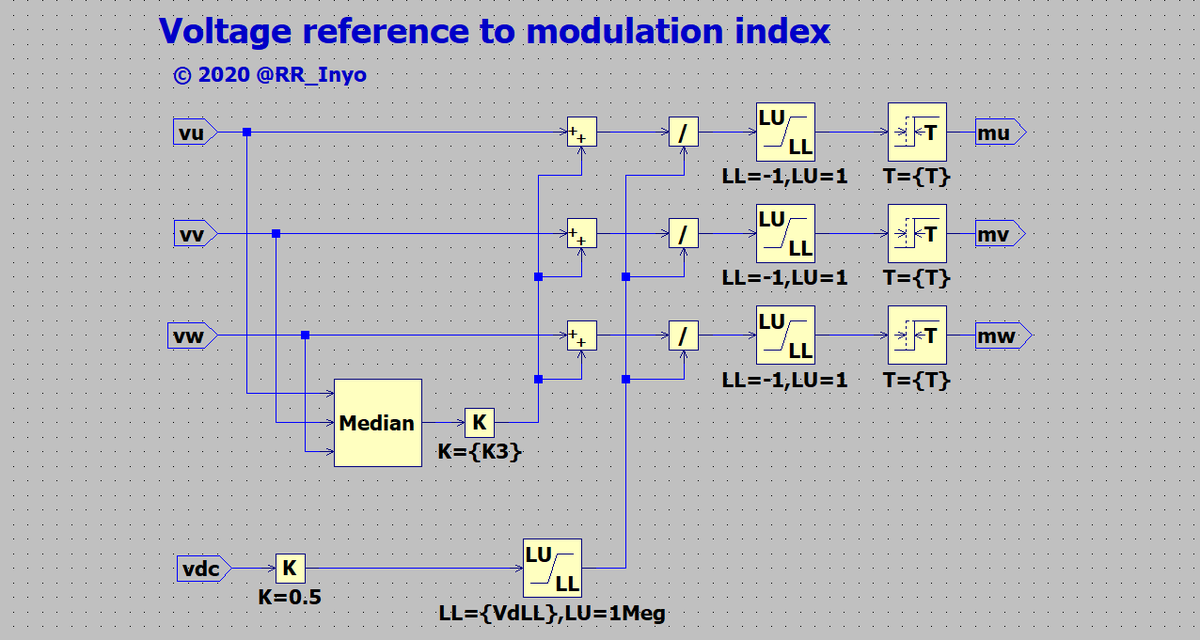
電圧指令値から変調波に換算する部分は図16の通りです。
基本的な考え方は,電圧指令値を直流電圧で割ってやることですね。
直流電圧と変調波の積が出力電圧になるので,まぁ,当たり前のことと言えると思います。
問題は,電圧指令値vu,vv,vwの中央値(median)のK3 = 1 / 2倍を元のvu,vv,vwに加算している部分です。
これによって,インバータが同じ線間電圧を出力する場合の変調率(変調波の最大値)を倍に低減できます。
逆に言うと,同じ変調率でより大きな線間電圧を出力できるので,インバータの容量*21向上が可能です。
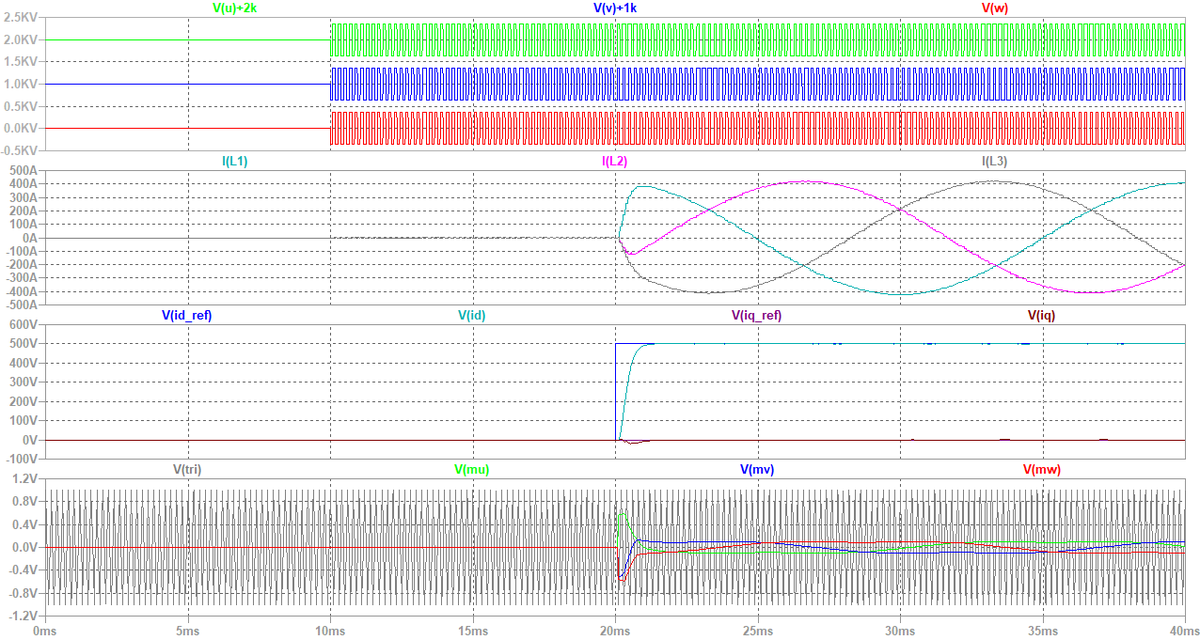
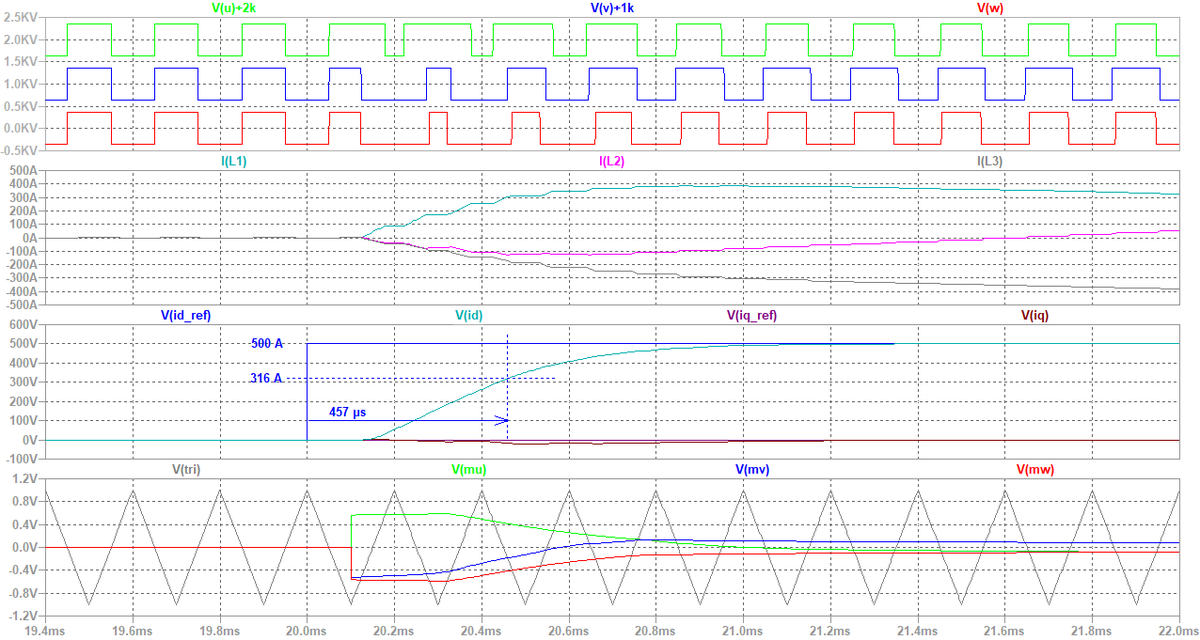
シミュレーションを実行すると,図17が得られます。図18は図17の拡大図です。 ここでは,結果を分かり易くするため,デッドタイムなしとしています。 d軸電流指令値id_refを時刻t = 20 msで500 Aにステップ状に立ち上げます。 d-q座標系では直流電流の制御ですが,三相に戻した電流波形(I(L1), I(L2), I(L3))を見ると,三相平衡な正弦波となっていることが判ります。 図18より,d-q座標系での電流制御の時定数はτ = 457 μsとなりました。 もし,T = 100 μsのサンプル & ホールドと1サンプル遅れがなければ,τ = 400 μsとなるので*22,妥当かと考えます*23。
ここで,デッドタイムとしてTd = 2 μsを考慮したシミュレーションを実行すると,図18は図19に変わります。
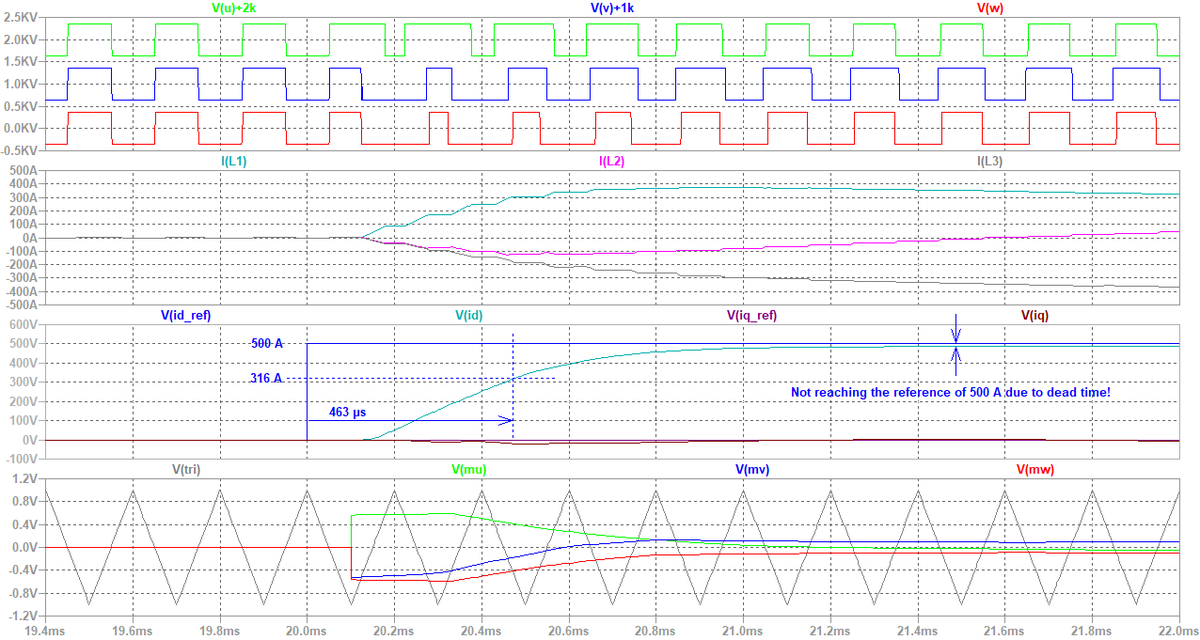
う~ん…。デッドタイムがあると,インバータの出力電圧に誤差が生じます。 具体的には,電流位相に同期した矩形波状の誤差電圧が生じ,近似的にはエネルギーを吸収する矩形波電圧源のように見えるんですよね…。 したがって,定常偏差が発生してしまいます。応答も若干遅くなっていますね。 ただしこれは,交流系統がないために,誤差電圧が相対的に大きく見えているためでしょう。
以上で,d-q座標系での三相交流電流制御を作ることができました。
交流系統に連系する
いよいよ交流系統に連系しますが,図16に追加すべきは,交流系統に相当する三相電圧源の追加と, いわゆる系統電圧フィードフォワードのみです。
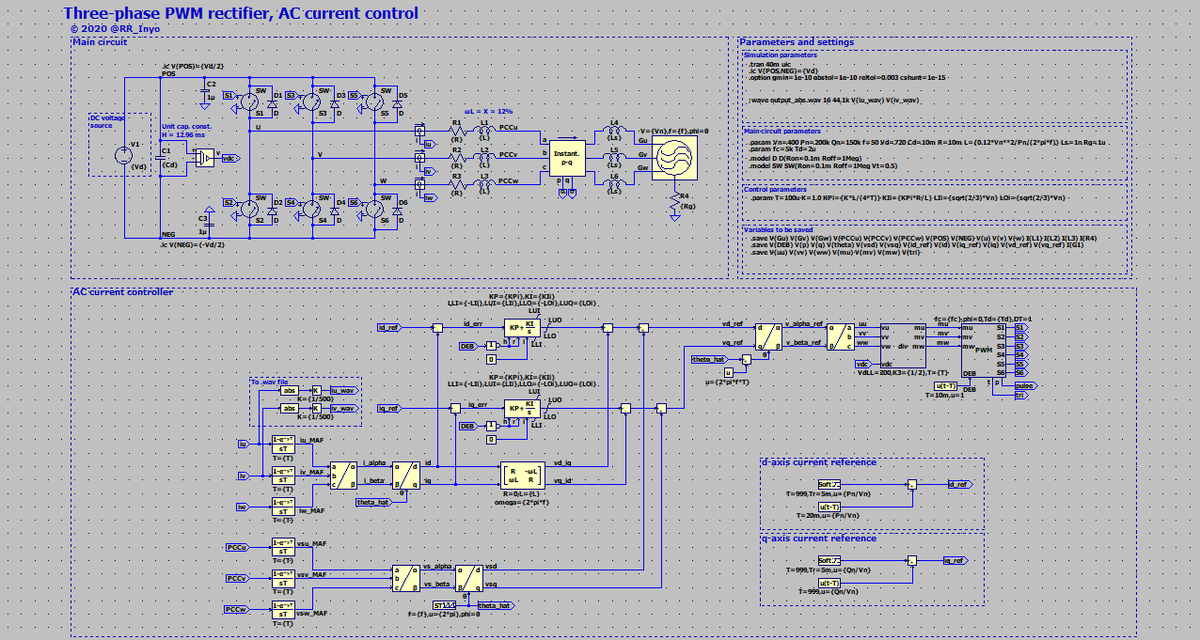
図19に,交流系統に相当する三相電圧源と系統電圧フィードフォワードを追加したschematicを示します。 ここで,系統電圧フィードフォワードとは何か,簡単にご説明します。 本ブログの前記事*24に記載したように,系統連系変換器の電流制御にとって,交流系統の電圧は「外乱」として考えることができます。 幸い,図3(Zs = 0の場合)や図14では,RとLの向こう側の電圧vsu, sv, swを電圧センサで計測することができます*25。 したがって,計測したvsu, sv, swをあらかじめインバータの電圧指令値にフィードフォワード制御として足し込んでおくことで,「外乱」を抑制できます。 また,別の考え方として,制御したいのは図1(b)のフェーザ図にも示した通り,交流系統とインバータの差電圧なので,最初から基準として交流系統と同じ振幅,周波数,位相の電圧を出力しておく,というように捉えることもできますね。
ここで,図19の直流側にも図12,16と同じく,直流電圧源を接続しています。 そう! まだまだPWM整流器にはなってませんので,ご注意下さい。
さて,図19のシミュレーションを実行すると,図20を得ます。
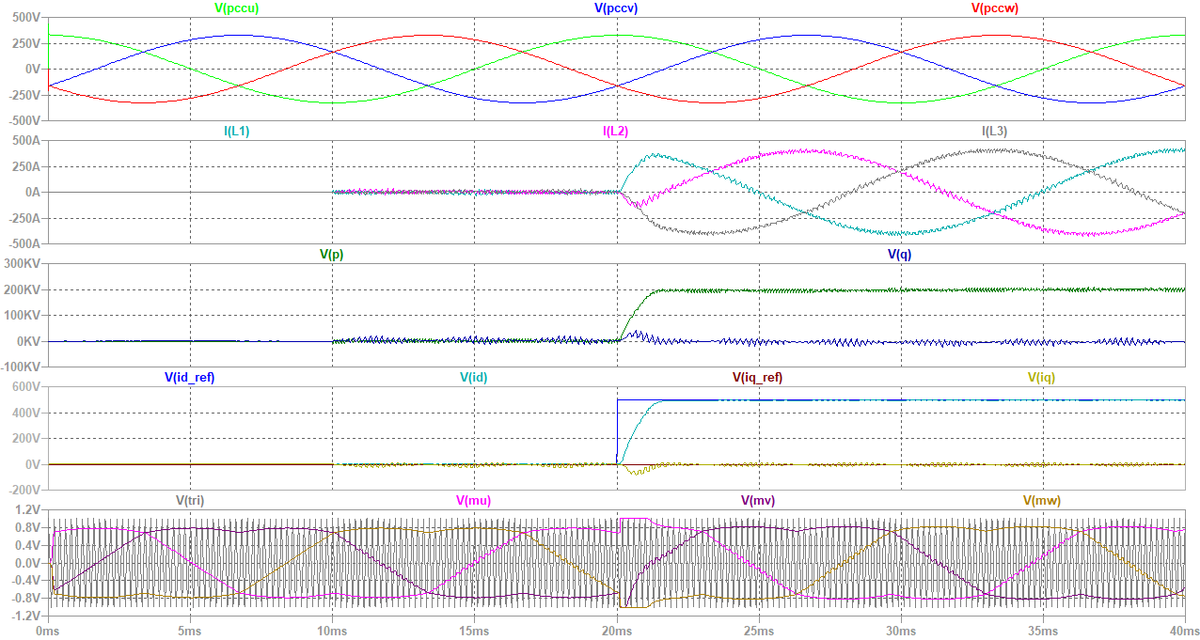
前節と同じく時刻t = 20 msでd軸電流指令値を500 Aまでステップ状に立ち上げています。 2段目の波形から分かるように,このとき,交流系統に対してp = 200 kWの有効電力を供給しています。
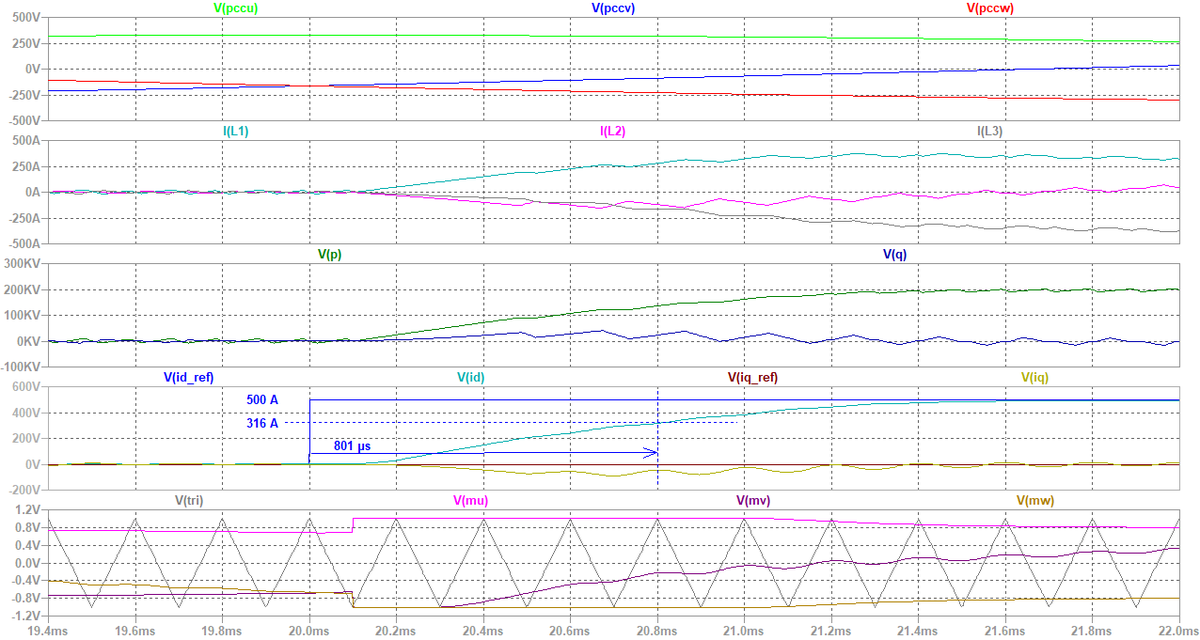
図20のステップ変化の近傍を拡大すると図21となります。 時定数τ = 801 μsとなっており,図18と比較すると2倍近く遅くなっています。 これは,最下段の波形を見ると判る通り,PWMの変調率がリミッタである1に張り付いてしまっているためですね…。 直流電圧がもっと高ければ,図21の時定数は図18の時定数に一致することでしょう。 とは言え,十分に高速な応答と言えると思います。
以上で,インバータを交流系統に連系することができました。
直流電圧制御を実装する ~そしてPWM整流器へ~
ついに,直流側の電圧源を取り除いて直流コンデンサと負荷電流源に取り換え,直流電圧制御を実装します。 そう,ようやくPWM整流器と呼んでも良い状態になります。 制御についてあれこれ書こうと思っていましたが,紙面(画面?)の都合上,次記事に回すことにしました。 とりあえず,結果のみを示すことにします。
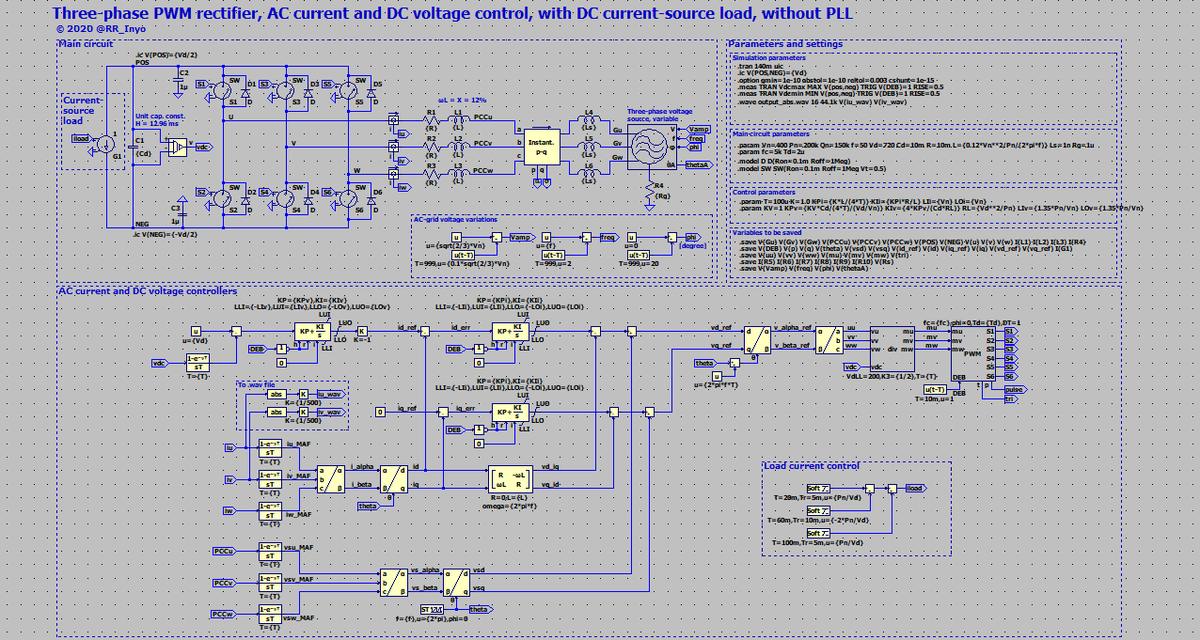
図22に直流側の電圧源の代わりに,10 mFの直流コンデンサと負荷電流源を接続した三相PWM整流器を示します。 負荷はもちろん抵抗器でも良いのですが,回生も試してみたいため,電流源(電圧制御電流源G1)としました。 電圧制御電流源G1の電流が正の場合は整流器として運転し,負の場合はインバータとして有効電力を系統に回生します。
直流電圧制御は,d軸電流制御の上位(外側)にもう1つ追加した,直流電圧をフィードバック制御するPI制御です。 今回,インバータから出ていく方向に電流の極性を定義してしまったため,直流電圧が足りない場合に交流系統から電力を吸い込むようにしたいため,PI制御器の直後に係数−1を置いています*26。
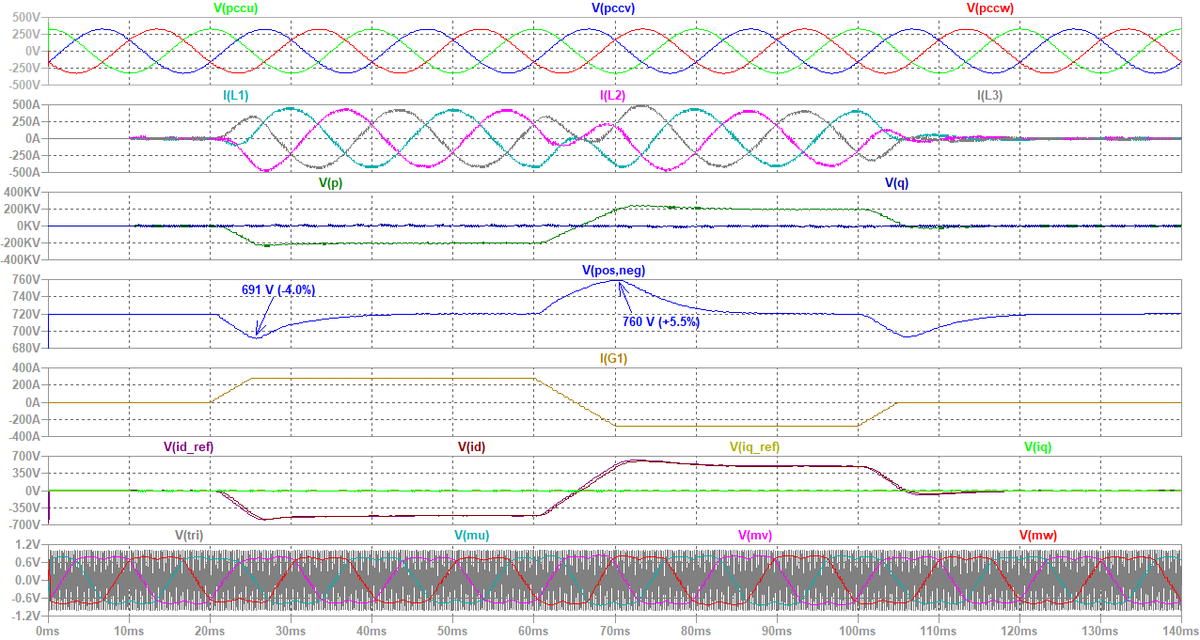
図23にシミュレーション波形を示します。 時刻t = 20 msで電圧制御電流源G1の電流を5 msのスロープで200 kW / 720 V = 277.8 Aまで立ち上げます。 すると,直流電圧を一定に維持するためのd軸電流指令値を,直流電圧制御が自動的に生成します。 時刻t = 40 ms ~ 50 msにかけて,でG1の電流を反転します。 いわゆる潮流反転です。
電流位相反転❗ 電力が逆流しています❗
と伊吹マヤさんが叫んでくれそうです(?)。 やはり,直流電圧制御も自動的に反転し,有効電力を交流系統に回生します。
時刻t = 100 msでG1の電流が零に立ち下がります。
直流電圧には,負荷電流(G1の電流)の立ち上げ時に4%,直流反転時に5%の変動を生じますが,積分ゲインのおかげで,定常的には指令値の720 Vに制御できていることが判ります。
以上で,直流電圧制御を実装して,三相PWM整流器を作ることができました。
PLLを追加する
前節では,まだ交流系統の電圧位相を検出するPLLを設けていませんでした。 そう,d-q変換のための位相角がいわゆる決め打ちだったのです。 しかし,実際の交流系統は位相も周波数も振幅も時々刻々変化します。 そこで,交流系統の電圧位相を検出するPLL(をはじめとする種々の方法)が必要です。 本記事では,
- S. Golestan, et al. "Three-phase PLLs: A review of recent advances," IEEE Trans. Power Electron., vol. 32, no. 3, Mar. 2017, pp. 1894-1907.
の図1に標準的な三相PLLとして記載されているブロック図を,図24のように実装しました。
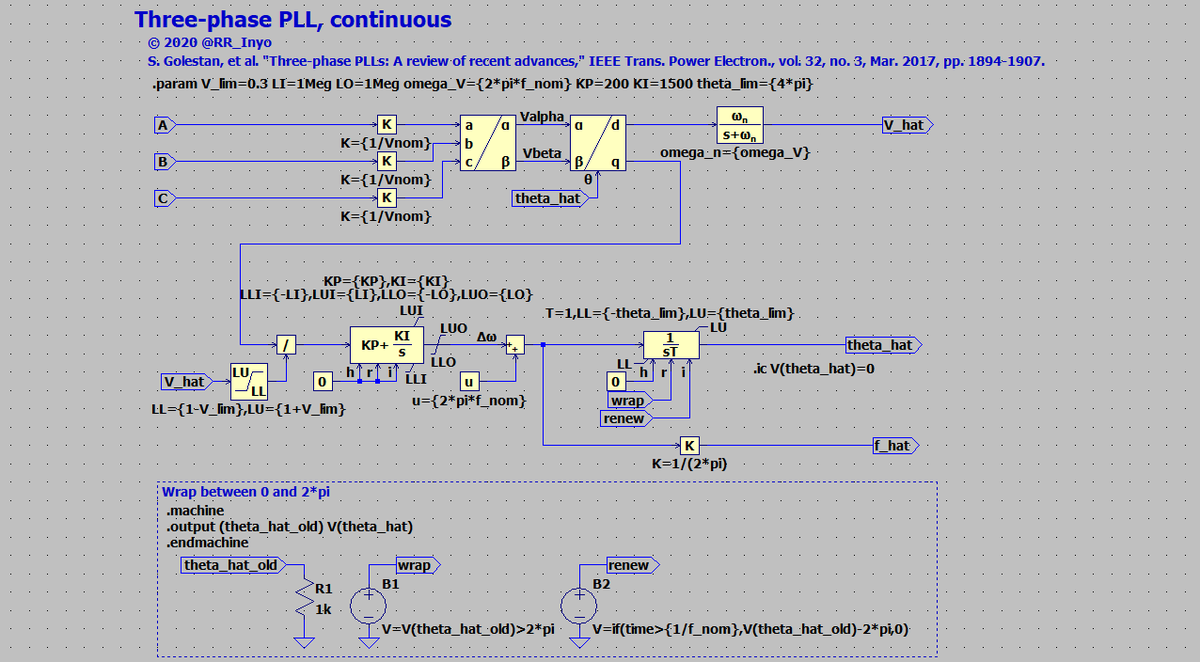
PI制御のゲイン? 恐縮ですが,トライ & エラーです…💦
図24を実装した三相PWM整流器が実は冒頭の図1となりますが,一番上までスクロールするのは面倒なので,図25として再掲します。


図24を階層化ブロックとして,図25の一番下の方に実装しています。
同じく,シミュレーション結果は冒頭の図2となりますが,これも図26として再掲しましょう。 時刻t = 20 msから,負荷である電圧制御電流源G1が電流を流し始めます。 時刻t = 60 msで位相+20°,時刻t = 100 msで周波数+2 Hz,時刻t = 140 msで振幅−0.05 p.u.の各急変がそれぞれ発生していますが,三相PLLが約20 msでそれぞれの急変に追従することにより,三相PWM整流器としての運転を安定に継続できていることが判ります。
以上より,本記事の目標である三相PLLを実装した三相PWM整流器を作ることができました。
まとめ
前記事の最後に,「今回の記事は,流石に長文過ぎましたので,次回はもっと気軽な短いネタを考えます💦」と書いたのですが,今回も異様に長い駄文を生成してしまいました💦 お付き合い下さった方,どうもありがとうございました。
とは言っても,制御系についてほとんど書けなかったので,次記事にて書いていこうと思っています💦
電流波形を聴く🎵
LTspiceでは,例えば電圧V(A)とV(B)をステレオのoutput.wavとして出力する場合,下記のようにドットコマンドを書きます。
.wave output.wav 16 44.1k V(A) V(B)
これで分解能16 bit,サンプリング周波数44.1 kHzの.wavファイルが生成されます。 なお,V(A)とV(B)は−1 V ~ +1 Vの範囲に入 っている必要があります(これ,結構な罠かもしれません)。
さて,私はここ数年,いやもう10年近く,PowerPointエンジニアとして暮らしており,せいぜいシミュレーションまでしかしない技術者になってしまったので,実験の雰囲気を感じたくて堪りません*27💦 そこで,本記事のPWM整流器におけるリアクトルの磁歪音を.wavファイルとして出力してみることにしました😁 ただし,磁気はN極でもS極でも鉄を引き付けるため,磁歪音は電流そのものではなく,その絶対値に関係するのではないかと思い,U相とV相の電流の絶対値をそれぞれ左チャンネルと右チャンネルとして出力してみました🔊
おおっ❗ かつて馴れ親しんだあのビ~~ッという基本波に,スイッチングに伴う鈴虫が重畳した音が聞こえるぞッ!
おまけ
LTspiceの波形ビューワは,ときどき崩れてしまうことがあります…。 図27に崩れた波形ビューワを示します。 これは,本記事の図13を作っている最中に崩れたものです。
節子「何でLTspiceの波形ビューワすぐ崩れてしまうん?」 pic.twitter.com/6cSg3Am8JE
— RR-いにょ (@RR_Inyo) 2020年8月27日
一体全体,何が起きているのかなぁ…?
*1:「系統連系はパワエレじゃない」とのご意見もTwitterで見掛けたことがあります…ちょっと悲しい…です…😥
*2:https://negligible.hatenablog.com/entry/2020/07/15/011258
*3:負荷電流を反転して回生もできるようにします。なお,PWM整流器なので,本来は(有効)電力を直流側で規定すべきなのかと思いますが,一般の系統連系インバータとして考えられるよう,今回は交流側で200 kWとしています。
*4:PCS = power conditioning systemは和製英語ですが…。
*5:本当はスイッチング周波数とインダクタンスからリプルを評価するなど,何らかの考慮しないといけないんでしょうが,今回は面倒なので考えないことにしました…💧
*6:加減乗除に「+」「-」「*」「/」を素直に使えず,すべて関数「IMSUM()」「IMSUB()」「IMPRODUCT()」「IMDIV()」となるため若干,いや,かなり面倒ですが…。
*7:いわゆる「3次重畳」を前提としています。
*8:実際には系統電圧が上昇している最中に容量性無効電力を出力する必要性はないと思いますが,図4を簡単な直方体にするため,っ本記事ではこのような仕様を考えました💦
*9:フィードバックを用いたより高度な制御もあり得ますが,ここでは考えません
*10:PWMはテキストベースのサブサーキット(subcircuit)としても作れますが,今回はschematicありの階層化ブロック(hiearchical block)としました。
*11:LTspiceではDEB < 0.5 Vの場合をFALSEと見なします。
*12:LTspiceなので本当の意味での「信号」という概念はなく,すべて電気回路なので,信号名に見えるmuやDEBは実際はノード名です💦 私の自作制御ライブラリContrailleでは,ノード名をあたかも信号名のように使います。
*13:あ,図9はテスト用の入力信号を削除してしまった後,つまり階層化ブロックにしてしまったものですね…。
*14:こんなんだから「パワエレじゃない」と言われるのかなぁ…😅
*15:LTspiceでは0をFALSE,1をTRUEとして扱っているので改善してほしいですね。
*16:図12中に見える「sqrt(3/2)」は相電圧ピーク値を線間電圧実効値に換算する係数です。
*17:考案したのはEdith Clarke (1883-1959)というアメリカ初の女性電気技術者です。彼女の伝記があれば読んでみたいですね。
*18:座標変換の数式を素直に読み解くと,α-β座標系の上で回転している電流を逆方向に引き戻して止めているようにも理解できますが,このようにイメージ化している記述には出会ったことがありません。
*19:同じく米国の技術者Robert H. Parkによって考案されたものです。
*20:この表現,あんまり見たことないですね…ちょっと斬新かも。
*21:個人的にこの言い方はあまり好きではありません…が,よく使われます。正確に言うと定格皮相電力ですよね。
*22:https://negligible.hatenablog.com/entry/2020/07/02/183822
*23:差である57 μsは解析的には得られないと思われます。
*24:https://negligible.hatenablog.com/entry/2020/08/12/051323
*25:実際は交流系統のインピーダンスZsが存在するので,実際は系統連系変換器の直近のPCCの電圧しか分かりません
*26:自作制御ライブラリContrailleで極性反転専用のnegateブロックを作っていたのを忘れていました…。
*27:かつては,主回路の組み立てから制御ハード・ソフト(C言語やIEC 60033-3),周辺CPLDやFPGAのVHDLまで(ものすごく幼稚ながらも)自分で書いていたんですが…あれはもう10年以上前の話…。