連続系の代表的な伝達関数の双一次変換による離散化
はじめに
連続系では1次遅れ要素や2次遅れ要素など,代表的な伝達関数というものがあります,例えば,
などですね。
制御器やフィルタなどをもともと連続系で考えていた場合,マイコンやFPGAに実装しようとする際には離散系に変換する必要が生じます。 このときのテクニックのひとつに双一次変換(bilinear transformまたはTustin transformとも)があります。これは,
として,領域の伝達関数を
領域の伝達関数に変換する手法です。ここで
はサンプリング周期です。
動機と方法
双一次変換については,各種教科書・参考書で「変換できる」という記述は見掛けるのですが,実際に(記号計算として)変換した結果はあまり見たことがありませんでした。 そこで,Pythonの数式処理ライブラリSymPyを用いて,計算してみることにしました。
結果
連続系の様々な伝達関数を双一次変換してみました。結果は下表をご覧下さい。
| 要素名 | 連続系における伝達関数 | 双一次変換に基づく離散系における伝達関数 |
|---|---|---|
| 積分要素 | ||
| 1次LPF (1) | ||
| 1次LPF (2) | ||
| 1次HPF (1) | ||
| 1次HPF (2) | ||
| 2次LPF | ||
| 2次HPF | ||
| 2次BPF | ||
| 2次BEF | ||
| 位相遅れ補償 | ||
| 位相進み補償 |
ただし,
です。
なお,SymPyでの数式処理については,GitHubにJupyter Notebookを置いておきましたのでご興味がございましたらご覧ください。
ただし…! 微分要素は意図したとおりに動いていないので,このブログの上表からは除いてあります…!
LTspice XVIIへの実装と確認
後日このブログにも書きたいと思いますが,LTspiceでもステートマシンを記述する".machine"文をうまく使うと,サンプリングを(力技ながら)表現できます。
上表の領域での伝達関数は分母における
の0次の項が1となるように整理しています。
この場合,下記のすずむしさんのブログ記事のようにIIRフィルタを実装できます。
これをLTspiceに実装し,上記の変換表が正しいのかどうか,確認してみました。


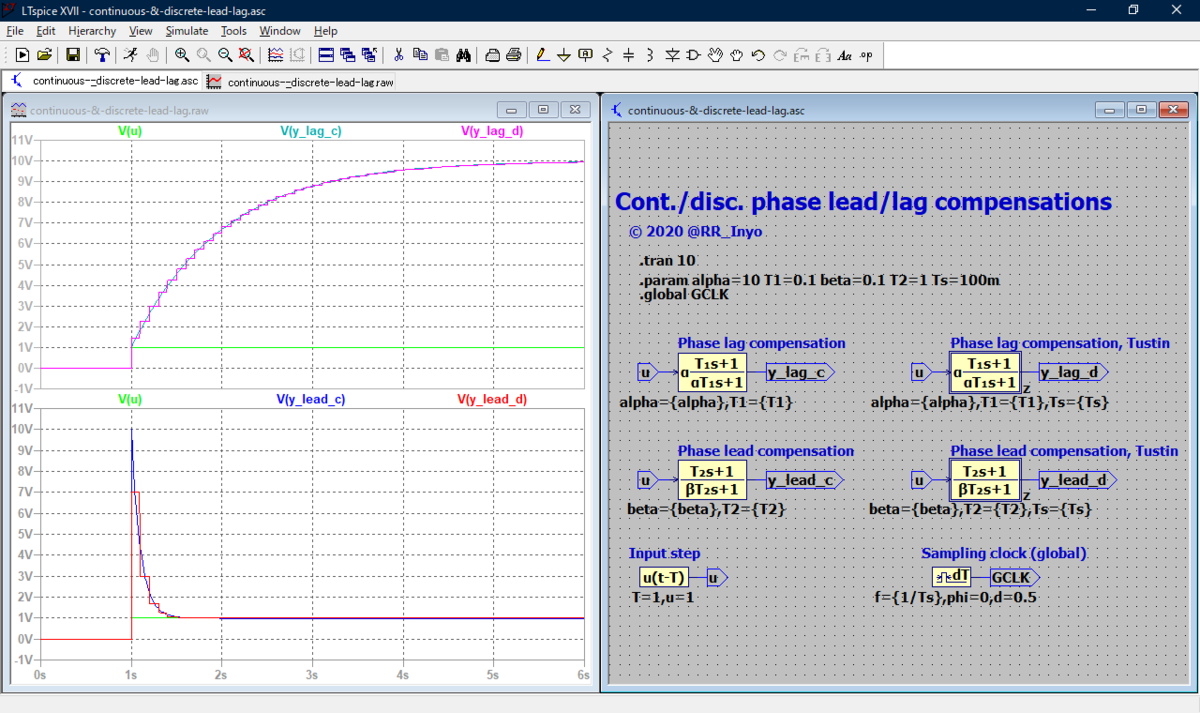
波形を見る限り,正しく動作しているように見えますね🎵